Математический спектр последовательности радиоимпульсов, периодичность которой нарушается за счет изменения начальных фаз импульсов.
При произвольном отношении частот ωр и W начальная фаза радиоимпульсов будет изменяться от периода к периоду. В этом случае условие u(t)=u(t+T) не выполняется, процесс становится не периодическим, хотя импульсы по-прежнему следуют с периодом T. Получить спектр такого процесса с помощью математического аппарата рядов Фурье для периодических функций уже нельзя. Такие радиоимпульсные последовательности называются почти периодическими. Рассмотрим два вида почти периодических радиоимпульсных последовательностей и способ получения их спектров. Будем называть их третьим и четвертым видами таких последовательностей.
Радиоимпульсную последовательность третьего вида можно получить, если «вырезать» радиоимпульсы из непрерывного колебания, но при этом не соблюдать кратности частот ωр¹kΩ (рис. 5.7,в1). В этом случае начальная фаза каждого (n-го) импульса будет зависеть от его номера в последовательности и будет равна 
.
Радиоимпульсную последовательность четвертого вида построим так, чтобы начальные фазы импульсов определялись некоторым сторонним колебанием с частотой ωП (рис. 5.7,г1). В этом случае начальная фаза каждого (n-го) импульса зависит от фазы этого колебания в момент начала импульса и будет равна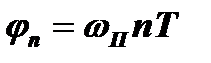 
. Периодичность последовательности будет определяться соотношением частот ωП и W. В частном случае при ωП=kW последовательность станет периодической.
И, наконец, радиоимпульсная последовательность пятого вида может быть получена в том случае, когда начальные фазы импульсов определяются некоторыс случайным, шумовым процессом.
Напомним, что спектр периодической последовательности мы определяли по схеме:
| Периодический процесс, как функция времени. |
| Расчет коэффициентов ряда Фурье |
| Периодический процесс, как сумма частотных гармоник. |
Для определения спектра почти периодической последовательности схема будет иной: находится спектр одного импульса, а спектр всей последовательности определяется как сумма спектров всех импульсов, которые входят в ее состав:
| Функция, описывающая один импульс во времени. |
| Спектр одного импульса. |
| Сумма спектров всех импульсов. |
| Обратное преобразование суммарного спектра во временную область. |
| Функция времени, описывающая процесс суммой частотных гармоник. |
| Функция, описывающая один импульс во времени. |
| Спектр одного импульса. |
| Сумма спектров всех импульсов. |
| Обратное преобразование суммарного спектра во временную область. |
| Функция времени, описывающая процесс суммой частотных гармоник. |
Один радиоимпульс с прямоугольной огибающей представим в виде:
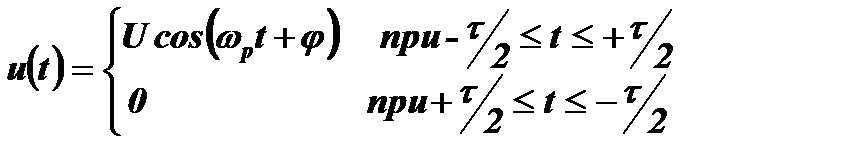
Спектр такого импульса будет равен:
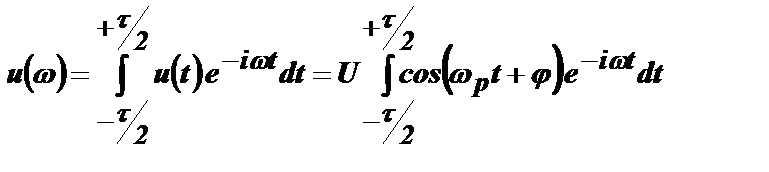
Учитывая, что: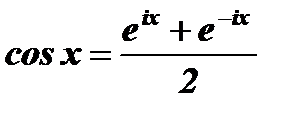 
, запишем: 
.
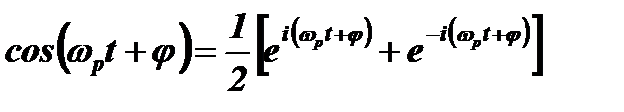Тогда:
.
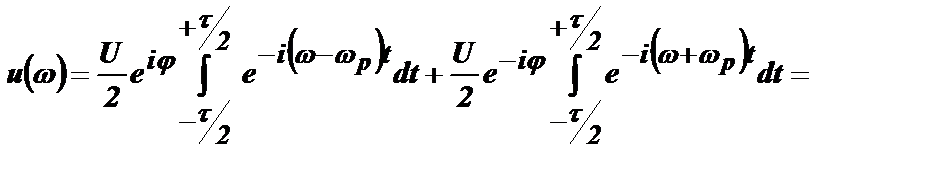
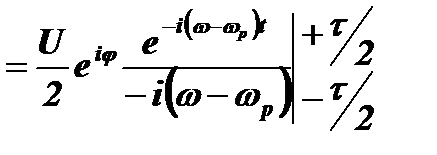
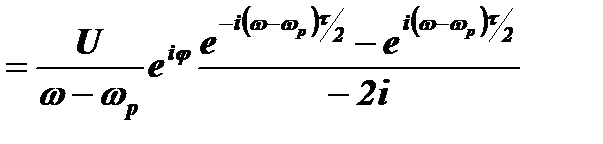
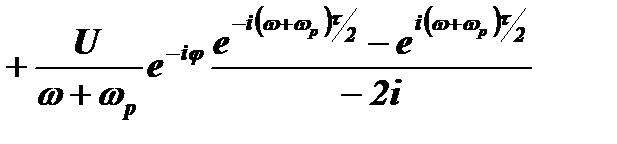Разделим числитель и знаменатель каждого слагаемого на –1, а затем на τ/2. Учитывая, что: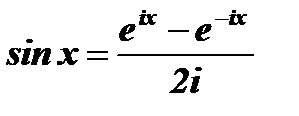 
, получим окончательное выражение для спектра одного радиоимпульса:
.
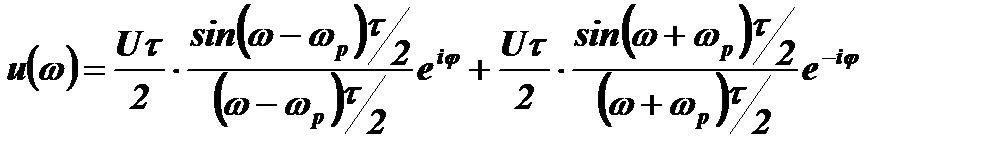Спектры разных импульсов почти периодической последовательности будут отличаться только разной начальной фазой, которой присвоим индекс, соответствующий номеру импульса в последовательности: jn. А тем частям формулы, которые не зависят от номера импульса, для сокращения дальнейшей записи присвоим обозначения:
; 
.
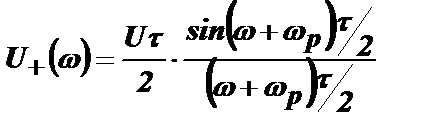Тогда спектр любого (n-го) импульса последовательности примет вид:
.
Теперь найдем спектры импульсов последовательности с учетом их запаздывания относительно начала отсчета времени t=0. Для этого используем теорему запаздывания из теории спектров, которая позволяет найти спектр смещенного (запаздывающего) импульса умножением его спектра на множитель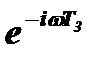 
, где Т3 – интервал времени между моментом t=0 и моментом появления этого импульса.
Импульс u0(t), появившийся в момент t=0, имеет спектр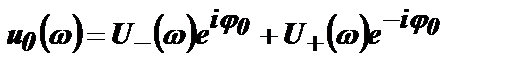 
. Спектр следующего импульса, смещенного относительно нулевого импульса на один период u1(t+Т) с учетом запаздывания имеет вид: 
.
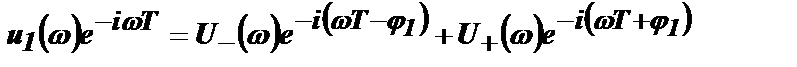Аналогично находятся спектры остальных импульсов последовательности.
Импульс u2(t+2Т) имеет спектр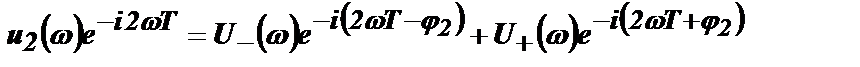 
. Импульс un(t+nТ) имеет спектр 
.
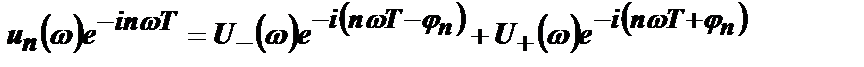Спектр всей последовательности радиоимпульсов можно представить в виде суммы:
.
.
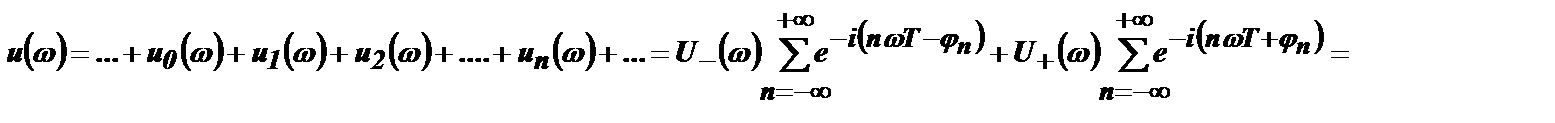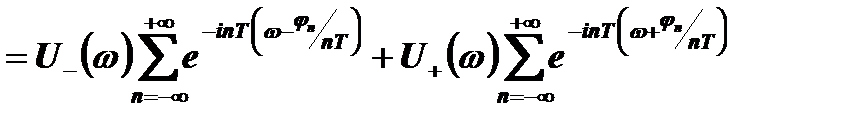Величина φn/nT имеет размерность частоты. Поэтому обозначим ее φn/nT= ωn
Из теории обобщенных функций известно, что:
, где δ – дельта функция.
Чтобы воспользоваться этой формулой заметим, что в выражении для u(ω) роль n играет (−n), а роль х играет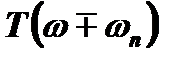 
. Тогда:
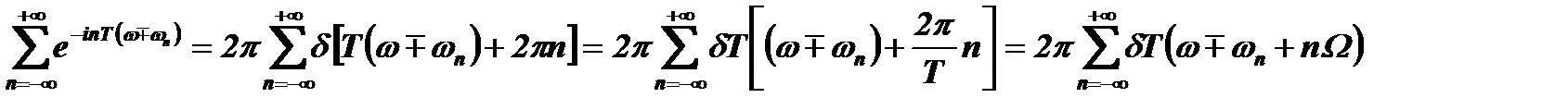
Учитывая, что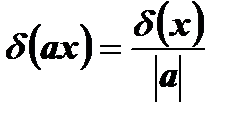 
, спектр последовательности примет окончательный вид:
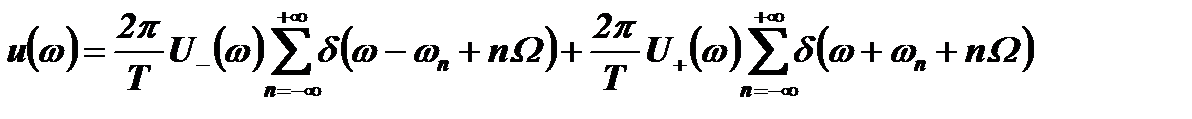
Чтобы представить почти периодическую функцию u(t) в виде ряда гармоник, подобного ряду Фурье для периодических функций, выполним обратное преобразование Фурье спектра u(ω).
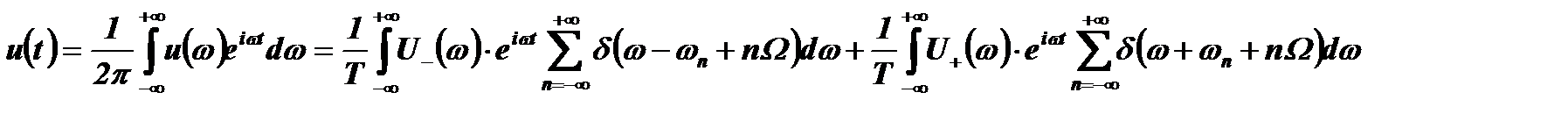
Изменим порядок суммирования и интегрирования:
.
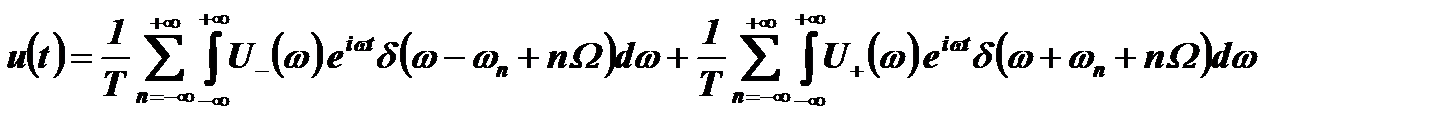Дельта функция обладает фильтрующими свойствами:
.
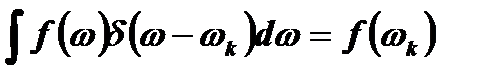В нашем случае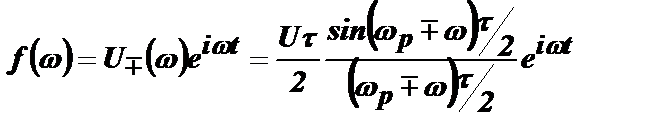 
, а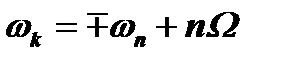 
.
Используя эти свойства δ-функции, получим выражение для u(t) в виде ряда гармоник:
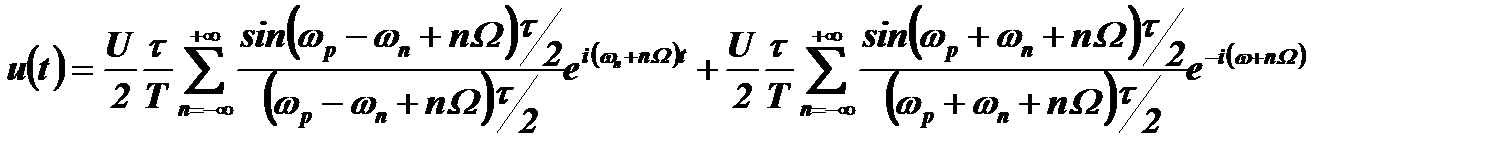
Напомним, что здесь n = ±1, ±2, ±3, .......
Это выражение дает нам ряд в комплексной форме. Нетрудно представить его в тригонометрической форме:
.
Из этого выражения видно, что спектр почти периодической функции имеет такую же структуру, как и спектр периодической функции, однако и огибающая спектра и его гармоники теперь зависят от ωn=φn/nT, то есть от параметра, нарушающего периодичность процесса - изменения начальной фазы высокочастотного заполнения от импульса к импульсу. Закон изменения начальной фазы определяет положение гармоник на оси частот.
Рассмотрим частные случаи почти периодических радиоимпульсных последовательностей.
Радиоимпульсная последовательность третьего вида. Начальная фаза в этом случае определяется частотой ωр. Тогда φn=ωpnT и ωn=φn/nT =ωp.
У спектра этой последовательности гармоники спектра расположены на частотах 
и, таким образом,«привязаны» к частоте заполнения импульсов ωр, в том числе и в тех случаях, когда она, в отличие от радиоимпульсной последовательности второго вида, не кратна частоте W (рис. 5.7, в). Счет гармоник начинается со значения частоты ω=ωр.
Максимум огибающей в этом случае не обязательно совпадет с положением гармоники. Поэтому здесь также можно раздельно изменять положение огибающей и положение гармоник на оси частот. Нули спектра находятся в точках 1/τ, 2/τ и т.д. При изменении частоты ωр гармоники перемещаются по оси частот, а огибающая остается неподвижной.
Радиоимпульсная последовательность четвертого вида. Начальная фаза каждого импульса определяется некоторым посторонним колебанием с частотой ωП: φn=ωПnT. Тогда φn/nT=ωП. У спектра этой последовательности гармоники спектра расположены на частотах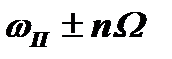 
и, таким образом,«привязаны» к частоте постороннего колебания ωП. В этом случае, положение гармоник спектра на оси частот не зависит от частоты заполнения ωр (рис. 5.7, г). Здесь также можно раздельно управлять положением огибающей на оси частот (меняя ωр) и положением гармоник (меняя ωП).
И, наконец, возможен случай, когда начальные фазы импульсов будут меняться от импульса к импульсу по случайному закону. Это – радиоимпульсная последовательность пятого вида. Независимо от номера импульса n начальная фаза может принимать любые значения в интервале от 0 до 2π, а величина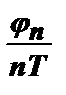 
- значения от nω до (n+1)ω. Отсюда следует, что каждая из гармоник спектра будет распределена равномерно в полосе частот от nW до (n+1)W. В этом случае спектр процесса будет сплошным в пределах огибающей (рис. 5.7, д).
Таким образом, различают пять видов радиоимпульсных последовательностей: два периодических, два почти периодических и один случайный.
Все пять видов радиоимпульсных последовательностей можно реально получить на выходе автогенератора, работающего в импульсном режиме.
Если начальная фаза очередного радиоимпульса определяется остаточным колебанием от предшествующего импульса, недостаточно погасшим к моменту его возникновения, а частоты ωр и W кратны, то возникнет периодическая радиоимпульсная последовательность первого вида.
Если начальная фаза каждого радиоимпульса определяется колебанием, возникший в контуре при подаче напряжения питания на автогенератор (ударное возбуждение контура), то возникнет периодическая радиоимпульсная последовательность второго вида.
Если начальная фаза очередного радиоимпульса определяется остаточным колебанием от предшествующего импульса, недостаточно погасшим к моменту его возникновения, но частоты ωр и W произвольны, то возникнет почти периодическая радиоимпульсная последовательность третьего вида.
Если начальная фаза очередного радиоимпульса определяется посторонним колебанием с частотой ωП, введенным извне в контур автогенератора, возникнет радиоимпульсная почти периодическая последовательность четвертого вида.
И, наконец, если начальная фаза колебания определяется только шумами в контуре автогенератора, то на его выходе будет радиоимпульсная последовательность пятого вида.
Дата добавления: 2016-04-19; просмотров: 1623;