Математический спектр периодической последовательности прямоугольных радиоимпульсов.

Радиоимпульс является одним из самых распространенных в радиотехнике сигналов. Поэтому изучение спектра последовательности радиоимпульсов представляет особый интерес.

Последовательность радиоимпульсов с прямоугольной огибающей, изображенную на рис. 4.41 в разделе 4.8, можно записать в виде выражения:

Здесь обозначены:

U,w_р = 2p¦_р; T_р =1/¦_р; t; j_n – амплитуда, частота, период, длительность и начальная фаза колебаний радиоимпульса;

W= 2pF; T = 1/F- частота повторения и период следования радиоимпульсов;

n = 1, 2, 3, ...– номер импульса.

В общем случае эта последовательность не будет строго периодической, так как на­чальные фазы импульсов j_n могут меняться от импульса к импульсу и ус­ловие периодичности функции – u(t)=u(t+T) – будет нарушено.

Этот общий случай мы рассмотрим ниже, а пока обратимся к частному случаю, когда функция u(t) будет чисто периодической и каждый радиоимпульс будет начинаться с одной и той же фазы j_n=j=const. Положим для определенности j_n=0.

Коэффициенты ряда Фурье этой периодической функции A_m, B_m и A₀ находятся по известным формулам (см. раздел 5.2). Индекс m = 1, 2, 3, ...означает номер гармоники.

Поскольку функция u(t) симметрична относительно оси времени, то А_o=0. Кроме того, мы выберем начало координат таким образом, что бы функция u(t) (косинус) была симметрична относительно оси амплитуд и являлась четной. Тогда и B_m =0, а, следовательно, и φ_m=0,

При принятых условиях ряд Фурье этой функции:

,

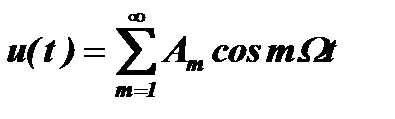будет определяться только коэффициентом А_m:

Это табличный интеграл. Его решение имеет вид:

.

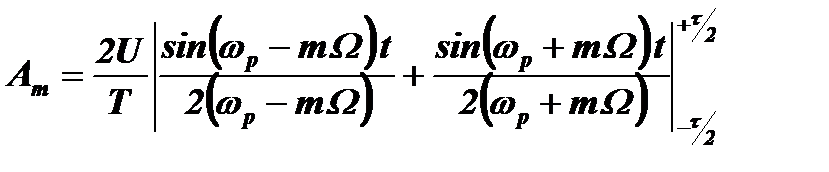Подставив пределы и разделив числитель и знаменатель на τ/2, получим:

.

Тогда ряд Фурье для функции u(t) примет вид:

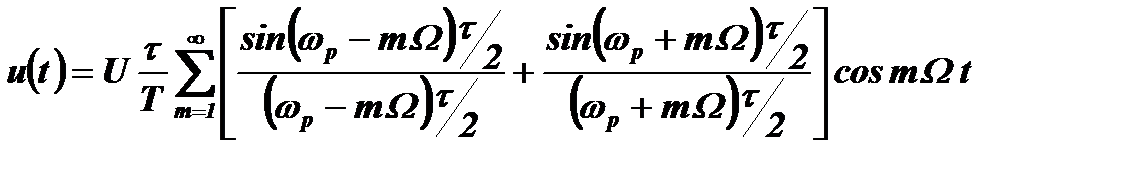
Таким образом, функцию u(t),являющуюся последовательностью импульсов во времени, мы представили теперь в виде последовательности частотных гармоник, которую в дальнейшем будем называть спектром этой функции (в действительности это не спектр в его классическом понимании, а просто другой вид представления сигнала u(t) во времени - см. раздел 5.4).

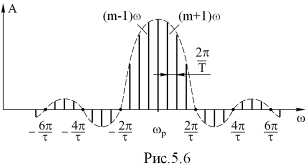
Из полученного ряда Фурье видно, что огибающая спектра периодической последовательности радиоимпульсов имеет вид sinx/x и совпадает по форме с огибающей спектра прямоугольных видеоимпульсов (рис. 5.6). Однако максимум огибающей переместился с нулевой частоты на частоту заполнения радиоимпульса ω_р. Гармоники спектра расположены на частотах ±mW. Счет гармоник начинается со значения частоты ω=0.

Периодическую последовательности радиоимпульсов можно получить двумя разными способами.

Можно «вырезать» радиоимпульсы из непрерывного гармонического колебания с периодом, кратным периоду высокочастотного заполнения радиоимпульсов Т=kТ_р (k - целое число), то есть ω_р=kW (рис. 5.7,а1). Полученный процесс назовем периодической последовательностью радиоимпульсов первого вида. Частоты ω_р и W жестко связаны между собой и поэтому максимум огибающей спектра совпадает с частотой гармоники kW, которая имеет максимальную амплитуду (рис. 5.7,а).Изменение любой из частот ω_р или W меняет одновременно и частотный интервал между гармониками и положение максимума огибающей спектра на оси частот.

Периодическую последовательность радиоимпульсов можно сформировать и при произвольном отношении частот ω_р и W (ω_р≠kW). Для этого необходимо выбрать любой радиоимпульс и «разместить» его копии на оси времени с периодом Т (рис. 5.7,б). Этот процесс назовем периодической радиоимпульсной последовательностью второго вида.

В спектре такой последовательности положение огибающей спектра, имеющей максимум на частоте заполнения импульсов ω_р, не связано с положением гармоник на оси частот. При изменении частоты ω_р перемещаться по оси частот будет только огибающая спектра. Гармоники же останутся на частотах mW. При изменении частоты W будет изменяться положение гармоник, а максимум огибающей спектра останется на частоте ω_р. Таким образом, положение огибающей спектра и положение гармоник на оси частот изменяются независимо. Это позволяет выделить из спектра периодической последовательности радиоимпульсов необходимую гармонику с максимальной амплитудой, переводя частоту заполнения радиоимпульсов ω_р на частоту этой гармоники (рис. 5.7,б).