Образование нулей в спектре последовательности прямоугольных видеоимпульсов.

Положение нулей в математическом спектре нетрудно определить, приравнивая нулю выражение для амплитуды тока в контуре (огибающей спектра):

.

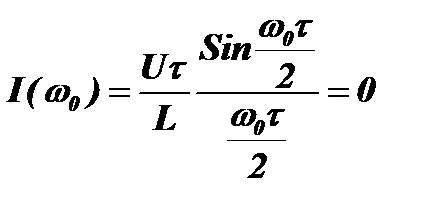Для этого достаточно положить 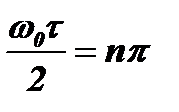, где n=1,2,3… Тогда: w₀t=2np, то есть 2pf₀t=2np, откуда 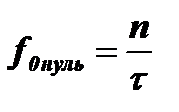. Это равенство и определяет положение нулей изучаемого нами спектра.

Чтобы понять, как физически образуются эти нули, рассмотрим условия, при которых амплитуда суммарного колебания, возбуждаемого в контуре передним и задним фронтами одного импульса, будет равна нулю. Очевидно, что это произойдет в том случае, когда эти колебания станут противофазными и компенсируют друг друга. Для этого необходимо чтобы: Dj_t=2p f₀t - p = (2n-1)p, где n =1,2,3…В этом случаеf₀t =n или 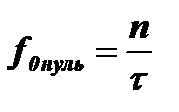, что совпадает с выражением, полученным из формулы для огибающей спектра.

При n=1 колебания будут отсутствовать на частотах 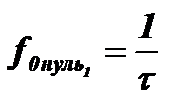.В этом случае один период колебания контура равен длине импульса t = Т₀.Колебание, вызванное передним фронтом импульса, достигнув заднего фронта, «встречает» колебание, вызванное этим фронтом и находящееся в противофазе. В результате эти колебания компенсируют друг друга и по окончании импульса колебания на выходе контура отсутствуют. Диаграмма колебаний для этого случая при Т=9Т_о=9tпоказана на рис. 5.4. На рис. 5.4,а показаны возбуждающие импульсы, а на рис. 5.4,б и 5.4,в – колебания, вызванные в контуре передними и задними фронтами импульсов. На рис. 5.4,г видно, что суммарное колебание в контуре отсутствует. Есть только ²всплески² в период прохода импульса через контур.

При других n колебания в контуре после окончания импульса будут отсутствовать на частотах:f₀ = n/ t.

Возможен случай, когда частота f_{0 нуль}, на которой произошла компенсация колебаний, оставшихся после каждого импульса, будет совпадать с резонансной частотой контура f₀=mF. Но гармоника спектра на этой частоте не возникнет, поскольку будут отсутствовать колебания, необходимые для ее формирования. Для этого случая 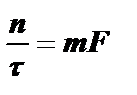или .

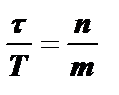Таким образом, положение нулей физического спектра полностью совпадает с положением нулей математического спектра.