Расположение частот физического спектра последовательности прямоугольных видеоимпульсов

При изучении в разделе 4.7 накопительного резонанса мы полагали длительность импульсов τ очень малой (намного меньше периода собственных колебаний контура Т_о) и не учитывали раздельного воздействия на контур переднего и заднего фронтов видеоимпульса. Тогда при Т=Т_о формировалась первая гармоника спектра (рис. 4.35) при Т=2Т_о образовывалась вторая гармоника спектра. Аналогично формировались и все последующие гармоники спектра на частотах, кратных частоте повторения импульсов f₀=mF.

Теперь рассмотрим процесс формирования гармоник физического спектрас учетом раздельного воздействия на контур переднего и заднего фронтов видеоимпульса. Анализ этого процесса разделим на два этапа. Сначала рассмотрим сложение колебаний, вызванных в контуре обоими фронтами одного видеоимпульса, и получим суммарное колебание, остающееся в контуре после его окончания. Затем вернемся к знакомому нам процессу сложения суммарных колебаний, остающихся в контуре после его возбуждения многими импульсами, и получим результирующее колебание в контуре.

Амплитуда суммарного колебания, оставшегося в контуре после окончания одного видеоимпульса, будет зависеть от разности фаз колебаний, вызванных передним и задним фронтами. Колебание,вызванное задним фронтом, отстает от колебания, вызванного передним фронтом, на угол j_t=w_оt=2pf_оt. Поскольку колебание от заднего фронта начинается с отрицательной полуволны, полный фазовый сдвиг между колебаниями, вызванными передним и задним фронтами, будет равен: Dj_t = 2p f_оt - p.

Своего максимального значения амплитуда суммарного колебания достигнет при синфазном сложении колебаний, возбужденных передним и задним фронтами импульса, то есть при выполнении условия Dj_t=2pf_оt-p=2pn. Это условие выполняется на частотах:

.

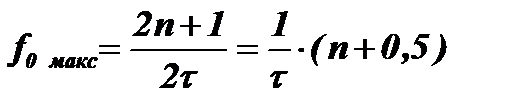В частности, первая максимальная амплитуда суммарного колебания образуется при n=0, когда 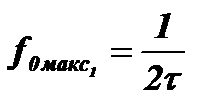или t = Т_о/2, а длительность импульса равна половине периода частоты контура (рис. 5.2).

Сложение суммарных колебаний, остающихся в контуре после его возбуждения многими импульсами (накопительный резонанс, формирующий гармонику спектра), будет происходить на частотах, кратных частоте повторения импульсов f₀ = mF.

В общем случае частоты f_0макс, на которых образуются максимальные амплитуды колебаний после каждого импульса, могут не совпадать с резонансными частотами контура f_о = mF. Таким образом, синфазное сложение колебаний, оставшихся в контуре после единичного импульса (зависящее от t) и синфазное сложение колебаний, оставшихся в контуре после многих импульсов (зависящее от T) выполняется при разных и не связанных друг с другом условиях.

Чтобы в частном случае частота гармоники совпала с максимумом огибающей спектра, необходимо одновременно выполнить условия: f₀=mF и , где m=1,2,3… и n = 0,1,2,3… Это произойдет, если f₀ =f_{0 макс}или:

.

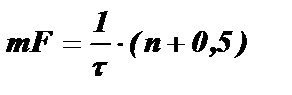Для этого необходимо, чтобы частота повторения была равна: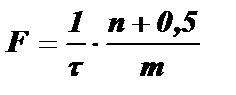

Диаграмма колебаний для этого случая при n = 0,m= 5, то есть при Т=5Т_о=10tпоказана на рис. 5.3.

На рис. 5.3,а изображены импульсы, возбуждающие контур. На рис 5.3,б и 5.3,в - колебания, возникшие в контуре под влиянием соответственно передних и задних фронтов импульсов, а на рис 5.3,г - общее суммарное колебание.

Из диаграммы колебаний на рис. 5.3, хорошо видно, что выделение гармоник физического спектра контуром при накопительном резонансе происходит не мгновенно. На накопление колебаний и образование гармоники требуется время, намного превышающее длительность импульса, возбуждающего контур. Это очень важное отличие физического спектра от математического.