Математический спектр периодической последовательности прямоугольных видеоимпульсов
Дальнейшее сравнение математического и физического спектров проведём на двух примерах: более простом - спектре последовательности видеоимпульсов, то есть импульсов без высокочастотного заполнения, и более сложном - спектре последовательности радиоимпульсов, имеющих такое заполнение.
Найдем математический спектр последовательности прямоугольных видеоимпульсов с амплитудой U, длительностью τ, следующих друг за другом с периодом T=1/F=2p/W (рис.4.32).
Приняв начало координат (t= 0) в середине импульса, запишем:
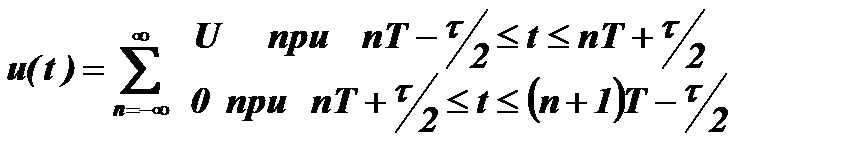 ,
,
где: n = 1, 2, 3, .......- целое число.
 Тогда:
Тогда:
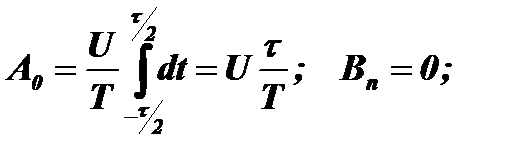
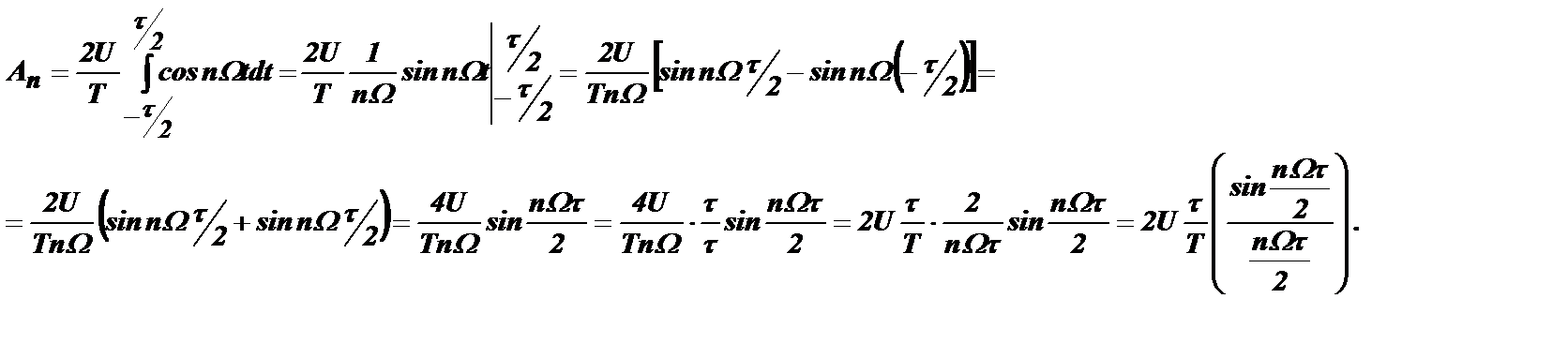
Величина Т/τ=Q называется скважностью, а величина Ao=U/Q - средним значением функции u(t).
Тогда: 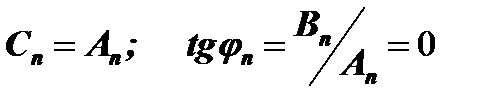 . Следовательно, величина φn может принимать значения 0,π,2π,... Тогда:
. Следовательно, величина φn может принимать значения 0,π,2π,... Тогда:
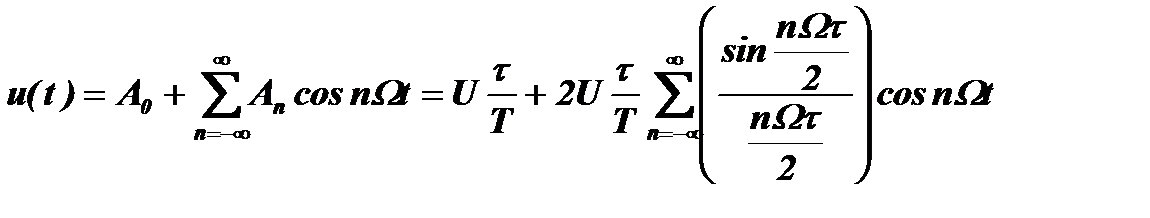 .
.
Общий вид спектра показан на рис. 5.1, а. На рис. 5.1, б изображен отдельно спектр амплитуд, а на рис. 5.1, в - спектр фаз.
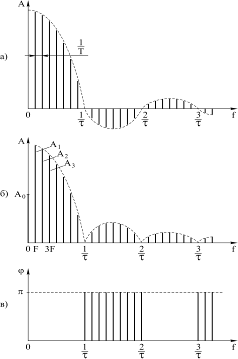
Рис. 5.1
Отметим основные четыре особенности математического спектра последовательности видеоимпульсов, поскольку в дальнейшем нас будет интересовать, как реализуются эти особенности в физическом спектре.
1. Огибающую спектра можно получить из выражения для амплитуд Аn, если перейти от дискретных значений частоты nW к текущему значению частоты w: 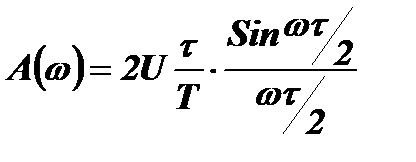 , то есть хорошо известной в математике функцией вида
, то есть хорошо известной в математике функцией вида 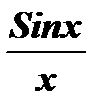 .
.
2. Гармоники спектра расположены на частотах nW или nF=n/Т, где n=0,1,2,3…
3. Положение нулей спектра нетрудно определить, приравняв нулю выражение для огибающей спектра. Для этого достаточно положить 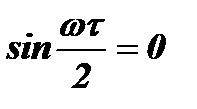 или
или 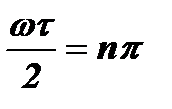 . Отсюда ωτ=2pn, а нули расположены на частотах
. Отсюда ωτ=2pn, а нули расположены на частотах 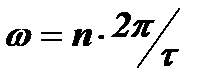 или f=n/τ.
или f=n/τ.
4. На частотах f=n/τ происходит изменение фазы гармоник спектра на ±p.
5.4. Спектр – математическое понятие
Представление сигнала в виде ряда Фурье, строго говоря, не является его спектром. Это просто другой вид представления данного сигнала во времени.
Чтобы получить математический спектр, необходимо произвести преобразование Фурье сигнала u(t): 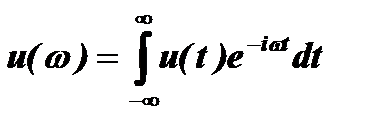 . Рассмотрим это преобразование для одной гармонической функции u1(t)=U1cos(Ωt+q1). Учитывая, что
. Рассмотрим это преобразование для одной гармонической функции u1(t)=U1cos(Ωt+q1). Учитывая, что 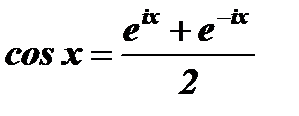 , спектральная плотность этой функции может быть представлена в виде:
, спектральная плотность этой функции может быть представлена в виде:
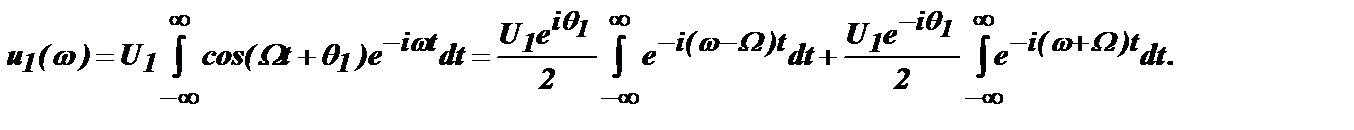
При такой записи мы можем воспользоваться известным выражением для дельта - функции:
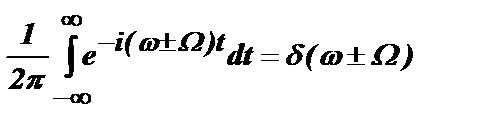 .
.
Тогда:
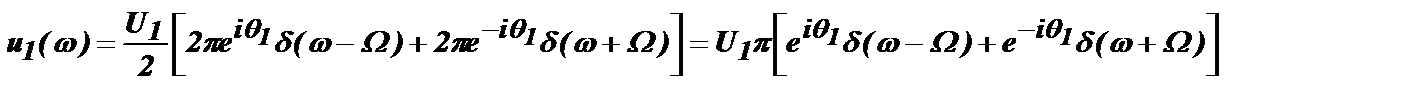 .
.
Эта функция равна нулю для всех частот, кроме w=Ω и w= –Ω, при которых u1(w) обращается в бесконечность. Таким образом, из этой формулы вытекает, что гармоническому колебанию с конечной амплитудой соответствует бесконечно большая спектральная плотность на дискретных частотах Ω и –Ω. При w=0 фаза q=0 и спектральная плотность сигнала на нулевой частоте будет равна: u(w=0)=U02pd(w). Распространив приведенное выше преобразование на все гармоники ряда Фурье, получим выражение для математического спектра периодического сигнала:
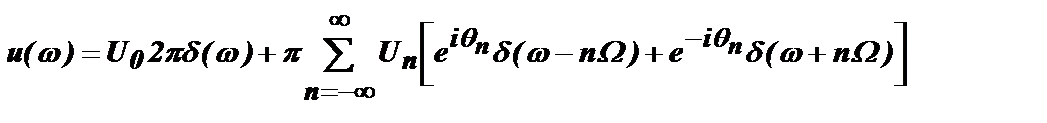 .
.
Пользоваться такой записью спектра бывает очень удобно при рассмотрении некоторых случаев, связанных с прохождением сигналов через радиотехнические цепи. Однако эта запись обладает меньшей наглядностью по сравнению с записью ряда Фурье для периодической функции. Действительно, что такое произведение Und(w-nΩ)? Это произведение конечной величины на бесконечно большую величину. Значит, это произведение есть бесконечно большая величина! И нас не успокаивает то обстоятельство, что у этой бесконечно большой величины конечная площадь (по определению дельта - функции). Представить себе это физически довольно трудно. Поэтому часто амплитудный спектр записывается не как набор произведений Und(w-Ω), а как набор коэффициентов Un. Намного проще представить себе гармонику ряда Фурье, которая является хорошо знакомой синусоидой с конечной амплитудой и конкретной частотой и фазой, чем дельта функцию. Поэтому обычно пользуются этим рядом и даже называют его спектром периодической функции, хотя истинно математическим спектром называется не ряд Фурье, а ряд смещенных дельта - функций. Все сказанное является хорошим примером того, как строгий математический подход иногда затрудняет физическое понимание явления или процесса.
Дата добавления: 2016-04-19; просмотров: 2368;
