Представление периодической функции в виде ряда Фурье
В прошлом веке Иван Бернулли, Леонард Эйлер, а затем и Жан-Батист Фурье впервые применили представление периодических функций тригонометрическими рядами. Это представление изучается достаточно подробно в других курсах, поэтому напомним только основные соотношения и определения.
Как уже отмечалось выше, всякую периодическую функцию u(t), для которой выполняется равенство u(t)=u(t+T), где T=1/F=2p/W , можно представить рядом Фурье:
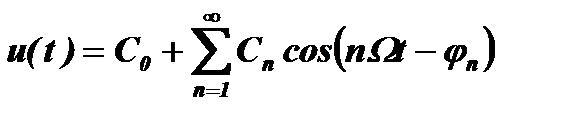
Каждое слагаемое этого ряда можно разложить по формуле косинуса для разности двух углов и представить в виде двух слагаемых:
,
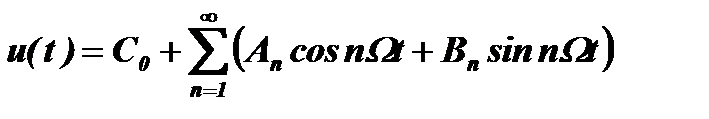где: An=Cncosφn, Bn=Cnsinφn, так что 
, а 
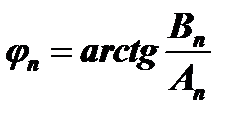
Коэффициенты Аn и Вn определяются по формулам Эйлера:
; 
.
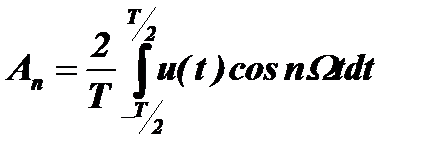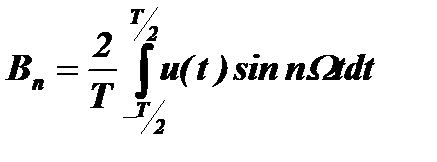При n=0:
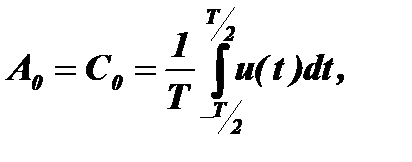а B0=0.
Коэффициенты Аn и Вn, являются средними значениями произведения функции u(t) и гармонического колебания с частотой nw на интервале длительностью Т. Мы уже знаем (раздел 2.5), что это функции взаимной корреляции, определяющие меру их связи. Следовательно, коэффициенты An и Bn показывают нам "сколько" синусоиды или косинусоиды с частотой nW содержится в данной функции u(t), разлагаемой в ряд Фурье.
Таким образом, мы можем представить периодическую функцию u(t) в виде суммы гармонических колебаний, где числа Cn являются амплитудами, а числа φn - фазами. Обычно в литературе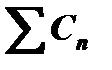 
называется спектром амплитуд, а 
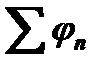- спектром фаз. Часто рассматривается только спектр амплитуд, который изображается в виде линий, расположенных в точках nW на оси частот и имеющих высоту, соответствующую числу Cn. Однако следует помнить, что для получения однозначного соответствия между временной функцией u(t) и её спектром необходимо использовать и спектр амплитуд, и спектр фаз. Это видно из такого простого примера. У сигналов 
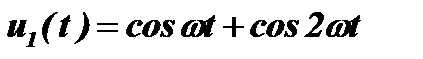и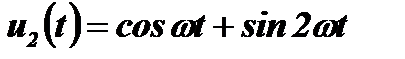 
будет одинаковый спектр амплитуд, но совершенно разный вид временных функций.
Дискретный спектр может иметь не только периодическая функция. Например, сигнал: 
не является периодическим, но имеет дискретный спектр, состоящий из двух спектральных линий. Также не будет строго периодическим сигнал, состоящий из последовательности радиоимпульсов (импульсов с высокочастотным заполнением), у которых период следования постоянен, но начальная фаза высокочастотного заполнения меняется от импульса к импульсу по какому-либо закону. Такие сигналы называются почти периодическими. Как мы увидим в дальнейшем, они также имеют дискретный спектр. Исследование физической природы спектров таких сигналов, мы будем выполнять так же, как и периодических.
Дата добавления: 2016-04-19; просмотров: 1440;