Резонанс в нелинейном колебательном контуре.

Явление резонанса в колебательном контуре, содержащем нелинейные элементы, имеет существенные особенности.

Рассмотрим сначала последовательный колебательный контур, активное сопротивление которого является нелинейным и зависит от амплитуды тока в контуре R(I). Для определенности положим, что при малых амплитудах тока в контуре величина этого сопротивления не изменяется. При увеличении амплитуды тока (например, при подходе к резонансу) величина сопротивления начинает увеличиваться. Это соответствует модели полупроводникового прибора, который при больших амплитудах входного напряжения переходит в режим насыщения. В этом режиме при увеличении амплитуды входного напряжения ток перестает расти, а сопротивление прибора увеличивается.

Сравним поведение нелинейного колебательного контура с контуром, все элементы которого линейны. Вдали от резонанса, при малых амплитудах тока поведение обеих контуров будет практически одинаково. Однако при приближении к резонансу и увеличении амплитуды тока в контуре, активное сопротивление контура начнет расти. Это приведет к тому, что на резонансной частоте (одинаковой у обоих контуров, поскольку L и С остаются постоянными) добротность нелинейного контура уменьшится. В результате ненормированная резонансная кривая нелинейного контура как бы "просядет" относительно резонансной кривой линейного контура.

Если нелинейное сопротивление контура имеет характеристику, при которой величина сопротивления уменьшается с ростом амплитуды тока в контуре, то эффект будет обратным. Максимум резонансной кривой нелинейного контура в этом случае будет выше, чем у линейного.

Картина резонанса в контуре существенно усложняется, если нелинейными элементами являются L или С.

Рассмотрим резонанс в последовательном колебательном контуре, содержащем нелинейную индуктивность L(i) (рис. 4.19).

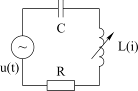
Рис. 4.19

В соответствии с законом Кирхгофа уравнение этого контура будет иметь вид: u_L+u_R+u_C=u или:

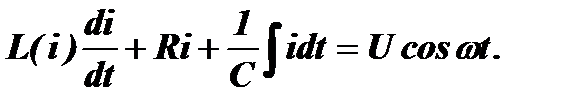
Это - нелинейное дифференциальное уравнение. Его точное решение вызывает большие затруднения.

Для решения такого уравнения обычно используется квазилинейный метод (метод первой гармоники), когда полагают, что контур обладает высокой добротностью и в режиме, близком к резонансу, из всех гармоник тока наибольшую амплитуду имеет ток первой гармоники I₁. Коэффициент нелинейных искажений k в этом случае будет невелик и действующее значение общего тока будет близким к амплитудному значению тока первой гармоники I₁. Таким образом, расчет проводится для токов и напряжений первой гармоники, но при этом учитывается, что индуктивность контура зависит от амплитуды этой гармоники, то есть L(I₁).

Тогда, по аналогии с линейным колебательным контуром, можно записать выражение для амплитуды первой гармоники тока в нелинейном контуре:

.

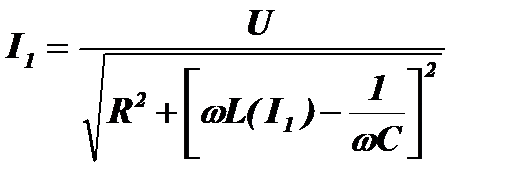При резонансе:

.

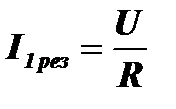Тогда нормированный безразмерный ток в нелинейном контуре 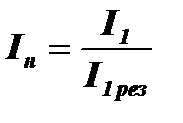имеет вид:

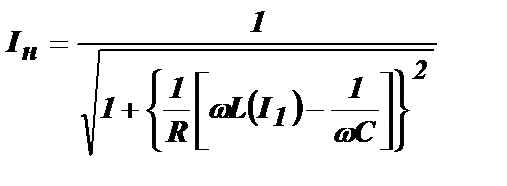
Теперь задача сводится к получению зависимости I_н от частоты или частотной расстройки.

Чтобы получить эту зависимость, необходимо аппроксимировать нелинейную характеристику L(I₁). Так как мы рассматриваем некоторый, не связанный с конкретной цепью, пример расчета, характер аппроксимации не имеет принципиального значения. Примем ее в виде укороченного полинома второй степени, который часто используется на практике для аппроксимации нелинейной индуктивности:

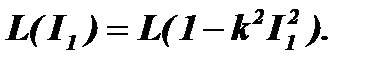
Здесь k - коэффициент, определяющий степень нелинейности характеристики индуктивности. При k=0 величина L(I₁)=L.

Из приведенных выше выражений видно, что резонансная частота нелинейного контура ω_он зависит от амплитуды тока I₁. Действительно:

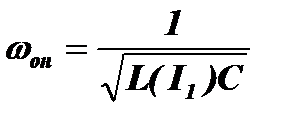
Подставив сюда аппроксимирующее выражение для L(I₁) получим:

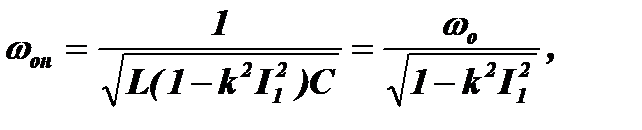
где 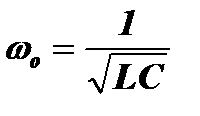- резонансная частота контура при k=0.

Таким образом, резонансная частота нелинейного контура ω_он при принятой аппроксимации 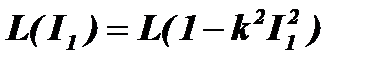возрастает с увеличением kI₁, то есть возрастает при увеличении тока I₁ (рис. 4.20).

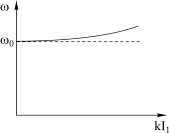
Рис. 4.20

В результате при увеличении частоты внешней ЭДС и при приближении ее к резонансу, ток I₁ будет расти, а резонансная частота ω_он, будет "убегать" все дальше вправо от значения частоты резонанса контура с постоянной индуктивностью ω_о. В результате рост тока будет продолжаться. Рассмотрим, каким образом при такой ситуации в нелинейном контуре возникает резонанс.

Так же, как это делается в теории линейного колебательного контура, ограничимся областью малых расстроек относительно резонансной частоты. Вспомним, что для линейного колебательного контура справедливо приближенное равенство (см. конец раздела 4.4):

.

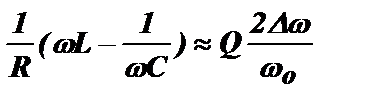В случае нелинейного контура ,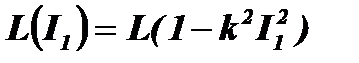

тогда: .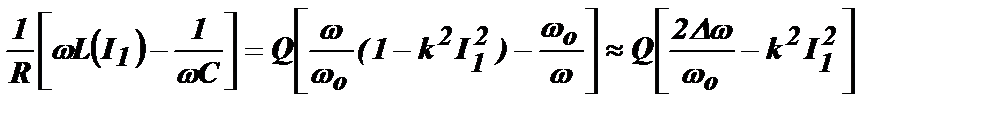

Подставим полученное выражение в формулу для нормированного тока:

,

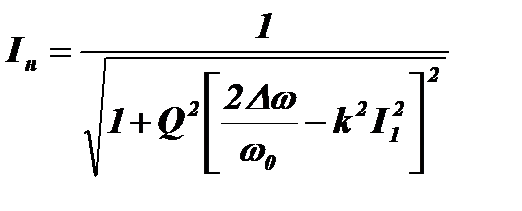Полученная формула отличается от резонансной характеристики линейного контура присутствием в знаменателе слагаемого .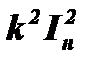

Это уравнение можно представить в виде зависимости 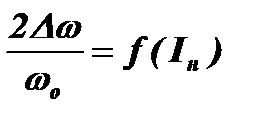. Решая уравнение относительно 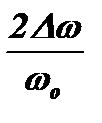, получим:

.

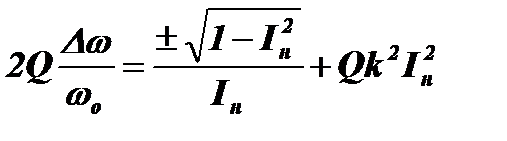По этой формуле рассчитаны и построены резонансные характеристики нелинейного колебательного контура (рис. 4.21).

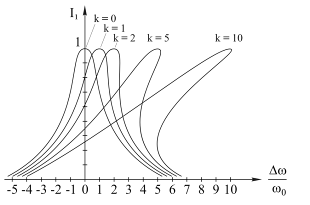
Рис. 4.21

При k=0 контур работает в линейном режиме и его характеристика совпадает с резонансной кривой линейного контура. С увеличением параметра k кривая деформируется. Ее максимум смещается в область более высоких частот, поскольку с ростом амплитуды I₁ индуктивность уменьшается, а резонансная частота контура растет.

После прохождения максимума и при дальнейшем увеличении частоты внешней ЭДС ток в контуре резко спадает. На этом участке сопротивление контура увеличивается не только из-за того, что реактивные сопротивления индуктивности и емкости перестают компенсировать друг друга. В дополнение к этому происходит уменьшение тока I₁, индуктивность контура растет и его резонансная частота начинает резко смещаться влево. Быстро растет расстройка между частотой внешнего сигнала ω и резонансной частотой ω_о. Однако пик резонансной кривой уже пройден и поэтому указанные явления приводят к деформации правой половины резонансной кривой, как показано на рисунке 4.21. "Впадина" в резонансной кривой проявляется из-за того, что "возврат" резонансной частоты контура в область более низких частот происходит быстрее, чем увеличение частоты ω, необходимое для снятия характеристики.

При реальном измерении резонансной характеристики нелинейного контура эту "впадину" получить нельзя (рис. 4.22).

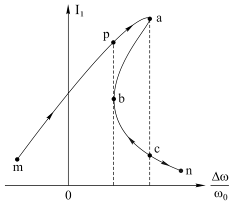
Рис. 4.22

Ток I_h не может "вернуться" к значению частоты, которой уже нет. Поэтому при увеличении частоты внешней ЭДС ω рабочая точка перемещается по участку mpa. Далее при увеличении частоты ω ток резко уменьшается и переходит в точку c кривой. После этого ток изменяется по участку cn. При изменении ω в обратную сторону (уменьшении) рабочая точка перемещается по участку кривой ncb, а в точке b происходит резкое увеличение тока и переход в рабочую точку p. Далее ток меняется в соответствии с участком кривой pm. Этот своеобразный "гистерезис" резонансной характеристики нелинейного колебательного контура наблюдается только при достаточно большой нелинейности (при больших значения коэффициента k).