Корреляция и резонанс. Согласованный фильтр.
Вернемся к формуле интеграла Дюамеля, позволяющей определить сигнал на выходе линейной системы во временной области в момент Т:
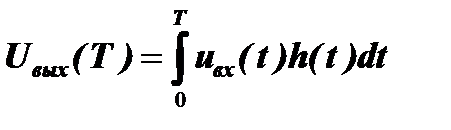
В этом случае корреляционный интеграл определяет степень взаимной связи (корреляцию) входного сигнала uвх(t) уже не с опорным сигналомuоп(t), как это было раньше. Теперь под интегралом стоит произведение входного сигнала с импульсной характеристикой системыh(t), которая является ее выходным сигналом, когда на вход подается единичный импульс δ(t). Поскольку единичный импульс никак не связан с входным сигналомuвх(t), то и импульсная характеристика системыне является опорным сигналом в формуле корреляционного интеграла. Таким образом, мы вернулись к взаимокорреляционной форме корреляционного интеграла, который определяет степень связи между двумя разными сигналами. Поэтому устройство, построенное по этой формуле, не производит обнаружения «своего» сигнала среди других сигналов и шумов с помощью опорного сигнала, а решает иную задачу: определяет «сколько» входного сигнала пройдет через линейную систему на ее выход. Это тоже задача селекции, но селекции иного вида.
Рассмотрим сначала простой пример. В качестве линейной системы выберем последовательный колебательный RLC контур с высокой добротностью.
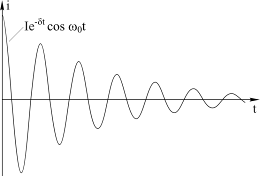
Рис. 2.7
Импульсной характеристикой такого контура является ток (рис. 2.7.), возникающий в нем при подаче на вход единичного импульса напряжения:
 ,
,
где δ =R/2L, w02=1/LC.
В качестве входного сигнала uвх(t) выберем последовательность коротких импульсов (рис. 2.8.).
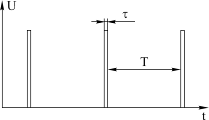
Рис. 2.8
Слово «короткий» означает, что длительность импульсов t мала по сравнению с периодом их следования Т, периодом собственных колебаний контура Т0=2p/w0 и постоянной времени контура t0=1/δ. При таких условиях эти импульсы могут быть представлены как единичные. Таким образом, входной сигнал uвх(t) может быть представлен, как последовательность единичных импульсов.
Каждый импульс вызывает в контуре колебаниеh(t) с частотой w0, длительность которого определяется постоянной времени контура t0. Поскольку в контуре с высокой добротностью δ<<w0, эта длительность будет намного больше и периода следования импульсов Т и периода собственных колебаний контура Т0. Тогда в контуре будет одновременно существовать большое число колебаний с частотой w0, которые будут складываться в соответствии с принципом суперпозиции. Сумма гармонических колебаний одной и той же частоты всегда является гармоническим колебанием этой же частоты. Поэтому в качестве выходного сигнала контура uвых(t) мы получим гармоническое колебание с частотой w0. Таким образом, из входной последовательности коротких импульсов uвх(t) контур «пропустил» на выход только колебание с собственной частотой w0. Так реализуется узкополосная селекция сигнала высокодобротным колебательным контуром.
Очевидно, что амплитуда суммарного колебания в контуре будет зависеть от соотношения фаз колебаний, вызванных отдельными импульсами входного сигнала. А это соотношение, в свою очередь, будет зависеть от соотношения периодов следования импульсов Т и собственных колебаний контура Т0. Когда будет выполняться условие T=nT0 (где n – целое число), колебания, вызванные отдельными импульсами входного сигнала, будут складываться в фазе. В этом случае амплитуда колебания в контуре с приходом каждого следующего импульса будет увеличиваться и перестанет расти только тогда, когда приток энергии начнет компенсироваться потерями в контуре. В контуре возникает резонанс. В переводе на спектральный язык это означает, что контур выделил одну из гармоник спектра входной последовательности коротких импульсовuвх(t).
В рассмотренном примере линейная система – колебательный контур – значительно изменила структуру входного сигнала: последовательность коротких импульсов превратилась в гармоническое колебание одной частоты.
Чаще на практике возникает задача, аналогичная той, которую решает коррелятор с опорным сигналом: пропустить входной сигнал uвх(t) через линейную систему без изменений, а все остальные сигналы, по возможности, не пропускать. Формула корреляционного интеграла Дюамеля подсказывает нам решение этой задачи.
Максимальная корреляция между входным сигналом и импульсной характеристикой линейной системы будет достигнута в том случае, когда эта характеристика будет равна входному сигналу h(t)=uвх(t). Тогда напряжение на выходе линейной системы будет равно:
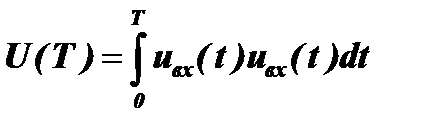 .
.
В более общем случаеэто равенство обычно представляют в виде: h(t)=kuвх(Tз–t), где k – коэффициент пропорциональности, а Tз– время задержки сигнала в линейной системе. В момент времени Т=Тз выходное напряжение представляет собой наибольшее значение функции автокорреляции входного напряжения, то есть система производит максимальное выделение входного сигнала. В этом случае линейная система, импульсная характеристика которой совпадает с входным сигналом, называется согласованным или оптимальным фильтром. На частотном языке смысл согласования заключается в том, что амплитудно-частотная характеристика согласованного фильтра совпадает с амплитудным спектром сигнала, а его фазо-частотная характеристика имеет знак, обратный знаку фазового спектра сигнала. Благодаря этому при Т=Тз все составляющие спектра принимаемого сигнала складываются в фазе и дают максимальный отклик.
Если на вход оптимального фильтра приходит смесь сигнала и шума  , то оптимальный фильтр, также как и коррелятор, обеспечивает наибольшее отношение сигнал/шум на выходе приемника. Таким образом, и коррелятор и согласованный фильтр при разном исполнении решают одну и ту же задачу.
, то оптимальный фильтр, также как и коррелятор, обеспечивает наибольшее отношение сигнал/шум на выходе приемника. Таким образом, и коррелятор и согласованный фильтр при разном исполнении решают одну и ту же задачу.
Различие между коррелятором и оптимальным фильтром заключается в том, что импульсная характеристика оптимального фильтра определяется его конструкцией и, в отличие от опорного сигнала коррелятора, не позволяет оперативно переходить к приему других сигналов. С развитием цифровых перестраиваемых фильтров это различие практически исчезает.
Рассмотренные примеры показывают, что процесс, описываемый интегралом Дюамеля и реализующий селекцию сигналов, распадается на две фазы, соответствующие структуре корреляционного интеграла. На первом этапе входной сигнал возбуждает линейную систему. При этом в ней возникает отклик, который позволяет "узнать", насколько ее собственное колебание совпадает с этим сигналом. На втором этапе происходит накопление этого отклика и при определенных условиях возникает резонанс. Таким образом, физическая картина резонанса в линейной системе и реализации оптимальной фильтрации описывается корреляционным интегралом.
Если внешнее воздействие и собственные колебания контура окажутся некоррелированы (или ортогональны), то резонанс не возникнет. Не ортогональность этих сигналов является обязательным условием резонанса.
В завершение этого раздела сделаем краткий вывод: интеграл от произведения двух функций, взятый на каком-либо интервале, позволяет всегда определить степень связи или степень зависимости этих функций на этом интервале и, благодаря этому, позволяет найти (выявить, узнать) неизвестную функцию с помощью известной.
Когерентность
Когерентность является одним из фундаментальных понятий радиотехники. Этим термином обозначается согласованное протекание нескольких колебательных процессов. Классическое определение когерентности, введённое более века назад, опирается на результаты следующих экспериментов. Возьмём два независимых генератора гармонических колебаний одной частоты. Будем измерять разность фаз между колебаниями этих генераторов (или фазу одного колебания относительно другого). Если эта разность фаз не меняется со временем, то колебания генераторов считаются когерентными. Если эта разность фаз со временем изменяется, то эти колебания называются некогерентными. Очевидным примером некогерентных колебаний являются колебания двух независимых шумовых генераторов. Измерения покажут, что разность фаз между их колебаниями будет всё время изменяться по случайному закону.
Позднее произошло расширение понятия когерентности. Для пояснения снова возьмём два независимых генератора гармонических колебаний, но теперь уже разной частоты. Разность фаз между их колебаниями будет постоянно изменяться с некоторой скоростью. Поскольку эта разность фаз всегда может быть определена для любого момента времени, такие колебания также стали относить к когерентным. Как видим, расширение понятия когерентности произошло за счёт того, что этим термином стало называться не только сохранение однозначной разности фаз между рассматриваемыми колебаниями, но и более общая степень связи между ними.
В последующие годы для определения степени когерентности колебаний стали использовать понятие корреляции. Рассмотрим энергию суммы двух взаимодействующих сигналов:
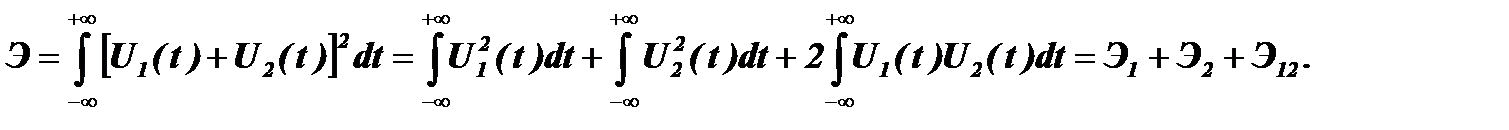
Первые два интеграла определяют энергию Э1 и Э2 каждого из сигналов S1(t) и S2(t), взятых отдельно, а последний, корреляционный интеграл – энергию взаимодействия Э12 между сигналами, которая и является мерой связи между ними. Чем больше энергия взаимодействия, тем выше когерентность сигналов U1(t) и U2(t). Введенная мера когерентности позволяет использовать ее для определения когерентности не только гармонических сигналов, но и сигналов, имеющих любую другую форму, в том числе сигналов, у которых вообще отсутствует такой параметр, как фаза и, соответственно, разность фаз (например, последовательность видеоимпульсов).
Также как и коэффициент корреляции, мера когерентности может быть нормирована к произведению абсолютных значений сигналов и по аналогии названа коэффициентом когерентности К.
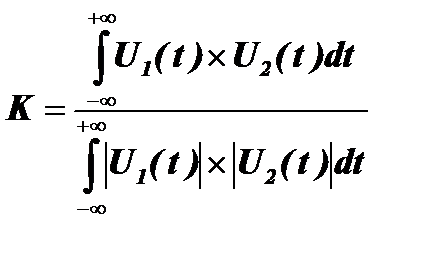 .
.
Величина К может принимать любые значения между –1 и +1.
Чтобы сигналы были не когерентны, необходимо, чтобы
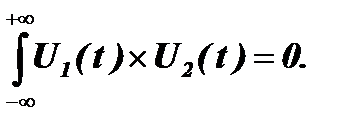
Нетрудно видеть, что это – условие некоррелированности или ортогональности сигналов. Следовательно, некогерентные сигналы являются некоррелированными. При сложении некогерентных сигналов энергия суммы сигналов равна сумме энергий отдельных сигналов.
В реальных радиотехнических системах, где когерентность колебаний необходима для выполнения системой своих функций, важным параметром является время когерентности. Это то время, за которое сохраняется необходимая (или заданная) степень когерентности между сигналами двух источников. По аналогии с взаимной корреляцией такая когерентность может быть названа взаимной когерентностью. Если речь идет об одном источнике, этот параметр показывает время, за которое сигнал источника сохраняет необходимую степень когерентности по отношению к моменту начала измерений. Такая когерентность может быть названа автокогерентностью.
Если источники сигналов возбуждаются от какого-либо третьего источника или синхронизируются его сигналом, то их когерентность будет "вечной". Но если источники сигналов независимы, то сохранить когерентность длительное время не удаётся. Дело в том, что любые реальные источники сигналов не могут долго сохранять идеальную стабильность параметров из-за влияния тепловых шумов, изменений режима электронных приборов и других факторов. Даже такие высокостабильные источники гармонических колебаний, как, например, кварцевые или квантовые генераторы, не могут сохранить монохроматичность своих колебаний в течение длительного времени. Частота этих генераторов медленно «плавает» в пределах некоторой полосы частот 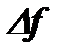 . Поэтому параметр
. Поэтому параметр 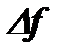 определяет стабильность частоты генератора. Чем уже полоса
определяет стабильность частоты генератора. Чем уже полоса 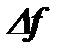 , тем стабильнее генератор. Следует учесть, что полоса частот
, тем стабильнее генератор. Следует учесть, что полоса частот 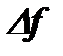 обычно определяется за некоторый период наблюдения ТН. В зависимости от продолжительности этого периода, стабильность частоты генератора называется кратковременной (например, секундной), длительной (например, суточной) и т. д.
обычно определяется за некоторый период наблюдения ТН. В зависимости от продолжительности этого периода, стабильность частоты генератора называется кратковременной (например, секундной), длительной (например, суточной) и т. д.
Временем когерентности называется величина 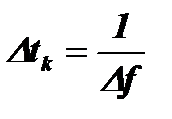 . Для источников гармонических колебаний необходимая или заданная степень когерентности обычно определяется разностью фаз, возникающей между колебаниями двух источников за время ТН, либо разностью фаз, возникающей между колебаниями одного генератора и виртуального, абсолютно стабильного генератора. Для источников произвольных сигналов необходимая или заданная степень когерентности определяется временным сдвигом между сигналами двух источников за время ТН, либо временным сдвигом сигнала одного источника за это время относительно сигнала виртуального, абсолютно стабильного источника. Чем стабильнее источники сигналов, тем больше величина Dtk и тем дольше сохраняется необходимая степень их когерентности.
. Для источников гармонических колебаний необходимая или заданная степень когерентности обычно определяется разностью фаз, возникающей между колебаниями двух источников за время ТН, либо разностью фаз, возникающей между колебаниями одного генератора и виртуального, абсолютно стабильного генератора. Для источников произвольных сигналов необходимая или заданная степень когерентности определяется временным сдвигом между сигналами двух источников за время ТН, либо временным сдвигом сигнала одного источника за это время относительно сигнала виртуального, абсолютно стабильного источника. Чем стабильнее источники сигналов, тем больше величина Dtk и тем дольше сохраняется необходимая степень их когерентности.
Когерентность является важной для тех радиотехнических систем, где фазовые соотношения сигнала на каком - либо отрезке времени используются в качестве рабочего параметра. Типичным примером являются системы череспериодной компенсации (ЧПК), применяемые в импульсных радиолокаторах и предназначенные для обнаружения цели на фоне пассивных помех. Метод ЧПК основан на сравнении (вычитании) импульсов, принятых в соседних (или более отдаленных) периодах повторения. Первый импульс, отражённый от целей и помех и принятый радиолокатором, задерживается на время, равное (или кратное) периоду повторения. После задержки этот импульс поступает на устройство компенсации одновременно со вторым импульсом, отражённым от тех же целей и помех. Если цели или помехи неподвижны, то импульсы, принятые в соседних периодах повторения, будут совершенно идентичны, на выходе системы компенсации будут появляться одинаковые по амплитуде импульсы, которые будут «удаляться» фильтрами нижних частот, как постоянная составляющая. Если же цель движется и имеет радиальную скорость, то за период повторения она приблизится к радиолокатору и второй импульс вернется через время, меньшее, чем время возвращения предыдущего импульса. В результате при вычитании импульсов, принятых в соседних периодах, на выходе системы вычитания появятся импульсы с изменяющейся во времени амплитудой. На выходе фильтра системы появится сигнал, свидетельствующий о наличии движущейся цели. Импульсы же, отраженные от неподвижных или малоподвижных пассивных помех, по-прежнему будут скомпенсированы.
Если же в системе ЧПК за время периода повторения импульсов произойдёт нарушение когерентности, то при отсутствии движущейся цели на выходе системы ЧПК появится сигнал, так называемый, "остаток", который будет восприниматься как цель, создавая, по существу, ложную цель. Поэтому для когерентных систем такого типа, как ЧПК, должно выполняться неравенство 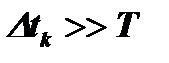 , где Т- период повторения импульсов или в более общем виде - рабочий интервал времени системы.
, где Т- период повторения импульсов или в более общем виде - рабочий интервал времени системы.
Резонанс
Введение
Резонансом называется резкий рост амплитуды колебаний в системе при вводе в систему энергии с помощью внешнего воздействия совершенно определенного вида.
Резонанс играет в радиотехнике особую роль. Благодаря резонансу осуществляется передача информации в большинстве радиотехнических систем. Именно резонанс позволяет "вырезать" узкий участок частотного диапазона, выделить необходимый сигнал из огромного многообразия сигналов, существующих одновременно в эфире или линии связи. Наиболее известен резонанс, возникающий в линейной колебательной системе с постоянными параметрами – RLC контуре или его аналоге – когда частота внешнего синусоидального сигнала совпадает с собственной частотой системы. Но почему он возникает при выполнении этого условия? Какие физические процессы происходят в колебательной системе и способствуют росту амплитуды? И единственный ли это случай значительного роста амплитуды колебаний в системе? Ведь известно, что резонанс может возникать в колебательной системе и при периодическом воздействии на нее негармонических сигналов. Причем – возникать на разных, хотя и кратных частотах. Какова в этом случае физическая природа резонанса? И отличаются ли условия возникновения этого вида резонанса от предыдущего случая?
А может быть возможны какие либо иные условия, при которых в системе возникает существенный рост амплитуды колебаний?
Мы постараемся дать ответы на эти вопросы.
Однако, чтобы досконально разобраться в поставленной задаче, нам придется начать издалека. Мы начнем с изучения элементов колебательной системы, их свойств и особенностей поведения в системе.
Основными элементами любой колебательной системы являются индуктивность и емкость, называемые также реактивными элементами. Они ведут себя по-разному при приложении к ним внешнего напряжения, что в основном, и определяет резонансные свойства колебательной системы. Рассмотрим эти элементы.
Индуктивность.
Для понимания физического существа резонанса нам необходимо разобраться в двух, связанных между собой, вопросах:
- от чего зависит сопротивление индуктивности переменному току?
- чем определяется сдвиг по фазе между напряжением на индуктивности и протекающим по ней током?
Вспомним хорошо известный эксперимент Фарадея, в процессе которого постоянный магнит перемещается относительно проволочного витка или катушки. Мы наблюдаем очень важное и для электротехники и для радиотехники явление – электромагнитную индукцию. При взаимном перемещении магнита и витка в проводе витка течет ток (индукционный ток), как будто бы мы подключили к этому проводу источник ЭДС. Но никакого источника там нет!
Фарадей установил, что ток в проводе витка появляется только при движении в системе "провод-поле" и что этот ток можно создать двумя способами: двигая провод при неподвижном магните или двигая магнит при неподвижном проводе. Эти два способа кажутся одинаковыми. Однако причины, приводящие к появлению тока в проводе, в этих двух случаях оказываются совершенно различными.
Если магнитное поле неподвижно, то при перемещении провода и пересечении им линий этого магнитного поля на каждый электрон с зарядом q в этом проводе возникает, так называемая, магнитная сила или сила Лоренца, пропорциональная скорости перемещения провода V и индукции магнитного поля B. Если силовые линии неподвижного магнитного поля и направление движения провода витка будут взаимно перпендикулярны и в свою очередь перпендикулярны самому проводу витка, эта сила будет толкать электроны вдоль провода, что приводит к возникновению индукционного тока (рис. 4.1).
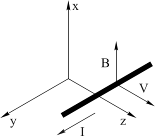
Рис. 4.1
Эта сила равна Fпров = q ∙ V ∙ B, а Лоренц получил это равенство на основе анализа экспериментальных данных.
Если магнит перемещается относительно неподвижного провода, то сила Лоренца не возникает. Но при движении магнитного поля всегда возникает электрическое поле Е, которое действует на электроны в неподвижном проводе с силой Fполе=q∙E. При этом в проводе возникает такой же индукционный ток, как и в первом случае.
Таким образом, одинаковый эффект для "движущегося провода" и "движущегося поля" вызывается совершенно разными силами взаимодействия. Вот что пишет известный американский физик Фейнман об этом явлении: "Мы не знаем в физике ни одного другого такого примера, когда бы простой и точный общий закон требовал для своего понимания анализа двух разных явлений. Обычно столь красивое обобщение исходит из единого глубокого основополагающего принципа. Но в этом случае какого-либо особо глубокого принципа не видно. Мы должны воспринимать закон Фарадея как одинаковый эффект от двух совершенно различных явлений" (Фейнмановские лекции по физике. т. 6, стр. 53).
С учетом этой особенности полная величина силы, действующей на электроны в проводе, определяется выражением F=Fпров+Fполе=q(E+V∙B). Величины, входящие в это выражение, векторные, так как необходимо учитывать направления взаимного движения поля и провода.
Возникновение тока в катушке при ее движении вдоль магнита или при движении магнита внутри катушки эквивалентно появлению в индуктивной цепи источника ЭДС. Поэтому действие магнитной силы или электрического поля на электроны в проводе Фарадей назвал наведенной ЭДС или ЭДС индукции.
Далее мы будем рассматривать только случай с движущимся магнитным полем и неподвижной катушкой, с которого начинал свои опыты Фарадей.
ЭДС индукции e, возникающую в одиночном проводе, Фарадей связал со скоростью изменения магнитного потока Ф простой формулой  . Это выражение Фарадей получил, анализируя результаты экспериментов.
. Это выражение Фарадей получил, анализируя результаты экспериментов.
Если катушка состоит из N витков, то формула Фарадея примет вид 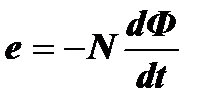 .
.
Совершенно естественно предположить, что индукционный ток, возникший под действием ЭДС индукции, вызовет вокруг катушки новое магнитное поле. Очевидно, что это вновь возникшее вторичное магнитное поле будет взаимодействовать с полем постоянного магнита, который перемещается в катушке.
Важным в этой физической картине является следующее. Вновь возникшее вторичное магнитное поле будет всегда направлено навстречу магнитному полю постоянного магнита. Поэтому в формуле Фарадея стоит знак минус. Это свойство вторичного магнитного поля определяется, так называемым, правилом Ленца, или "правилом потока".
Если первичный магнитный поток Ф от постоянного магнита растет, то вторичное магнитное поле будет противодействовать его росту.
Если первичный магнитный поток Ф от постоянного магнита уменьшается, то производная  поменяет свой знак на положительный. Вторичное магнитное поле при этом получит такой же знак, как и магнитное поле постоянного магнита и будет поддерживать это магнитное поле и противодействовать его уменьшению.
поменяет свой знак на положительный. Вторичное магнитное поле при этом получит такой же знак, как и магнитное поле постоянного магнита и будет поддерживать это магнитное поле и противодействовать его уменьшению.
Можно объяснить это явление также и через взаимодействие токов в проводе катушки. Изменяющееся вторичное магнитное поле вызовет вторичное электрическое поле. Это поле вызовет в катушке вторичную ЭДС индукции, которая в свою очередь создаст вторичный индукционный ток. Этот вторичный ток будет встречным, когда первичный ток увеличивается и попутным, когда первичный ток уменьшается. Он всегда будет препятствовать изменению первичного индукционного тока.
Уменьшение тока в цепи происходит точно так же, как если бы вместо индуктивности в цепь было бы включено сопротивление. Однако никакого сопротивления в данном случае физически не существует, есть лишь эффект подобный сопротивлению. Нет омических, джоулевых потерь на тепло, поскольку эффект сопротивления образовался за счет встречного индукционного тока, а не за счет поглощения электрической энергии в материале проводника.
Доказательство правила Ленца вытекает из закона сохранения энергии. Действительно, если бы вновь возникшее вторичное магнитное поле увеличивало изменение первичного поля постоянного магнита, то происходило бы возрастание индукционного тока, а он в свою очередь увеличивал бы снова магнитный поток. Процесс стал бы лавинообразным, даже если бы мы прекратили движение магнита. Мощность, выделяемая в этом случае в витке или катушке и равная i2R, стремилась бы к бесконечности, что несовместимо с законом сохранения энергии.
Причинные связи процессов, возникающих при электромагнитной индукции, удобно представить в виде диаграммы, показанной на рис. 4.2.
Следует помнить, что на диаграмме показаны причинные связи, а не последовательность событий. Разделение магнитных полей и токов на первичные и вторичные весьма условно и сделано для лучшего понимания физики явления. Реально же в витке или катушке сразу будет существовать суммарное магнитное поле и суммарный индукционный ток.
Обратимся теперь к случаю, представляющему наибольший интерес для исследования резонанса. Подключим катушку непосредственно к источнику переменного напряжения. Тогда возникший в катушке ток вызовет переменное магнитное поле вокруг и внутри катушки. Этот случай называется самоиндукцией. По уже знакомой нам схеме изменяющееся магнитное поле создаст электрическое поле, которое будет воздействовать на электроны в проводе катушки. Возникает ЭДС, которую теперь можно называть ЭДС самоиндукции и по правилу Ленца эта ЭДС вызовет индукционный ток, который течет в направлении, противоположном направлению первоначального тока, уменьшая его величину. Можно также считать, что индукционный ток создает магнитное поле, противоположное первоначальному полю, компенсирующее это первоначальное поле и гасящее его.
В этом случае причинные связи процессов будут выглядеть несколько иначе (рис. 4.3), поскольку здесь не внешнее магнитное поле вызовет индукционный ток, а ток в катушке, вызванный внешним источником напряжения, приводит к появлению магнитного поля.
| Напряжение внешнего источника |
| Ток в катушке, вызванный этим напряжением |
| Возникновение магнитного поля |
| Появление электрического поля |
| ЭДС самоиндукции, вызванная электрическим полем |
| Появление вторичного индукционного тока, направленного навстречу первичному току |
| Рис. 4.3. |
Еще раз напомним, что на диаграмме показаны причинные связи, а не последовательность событий и что в катушке реально существует одно суммарное магнитное поле и один суммарный ток.
И в этом случае ток в цепи уменьшается так же, как при включении в цепь активного сопротивления. Это свойство катушки называется реактивным, в данном случае индуктивным сопротивлением или импедансом. Импедансом также часто называют алгебраическую сумму активного и реактивного сопротивлений. Измеряется импеданс, как и обычное сопротивление, в омах.
Величина индуктивности. Импеданс будет тем больше, чем больше у катушки витков, по которым протекает ток, поскольку с увеличением числа витков растет величина магнитного поля, вызывающего индукционный ток. Магнитный поток Ф, пронизывающий N витков катушки, пропорционален току I в катушке. Коэффициент пропорциональности называется индуктивностью, определяется, как: 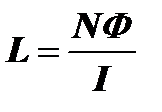 и измеряется в генри.
и измеряется в генри.
Выражение для мгновенного значения ЭДС индукции теперь можно записать следующим образом:
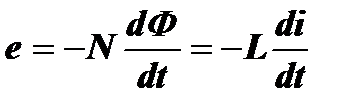
Из этой формулы видно, что ЭДС индукции, а, следовательно, и создаваемый ею вторичный индукционный ток и вызываемый им импеданс катушки будут увеличиваться с ростом скорости изменения первоначального тока в катушке. Очевидно, что эта скорость будет расти с увеличением частоты напряжения внешнего источника. Следовательно, импеданс катушки будет расти с увеличением частоты.
Теперь рассмотрим сдвиг по фазе между током и напряжением в катушке. Напомним, что ток, протекающий через активное сопротивление, подключенное к источнику ЭДС (рис. 4.4), вызывает на нем падение напряжения, точно равное ЭДС с обратным знаком.
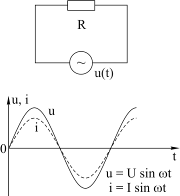
Рис. 4.4
Больше эта ЭДС – больше ток – больше падение напряжения. Меньше ЭДС – меньше ток – меньше падение напряжения. Поэтому ток и падение напряжения на активном сопротивлении всегда находятся в фазе друг с другом. Это подтверждает и закон Ома, в соответствии с которым активное сопротивление – постоянная величина, а это значит, что любое изменение тока сопровождается пропорциональным ему изменением падения напряжения.
По иному обстоит дело в индуктивности, подключенной к источнику переменной ЭДС.
Рассмотрим пример самоиндукции. Приложим к катушке гармоническое напряжение u=Ucosωt. Это напряжение должно уравновешиваться ЭДС индукции и по закону Кирхгофа:
u + e =0, т.е. u=− e, откуда  Тогда
Тогда 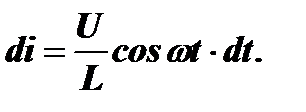
Интегрируя это выражение, получим значение тока: 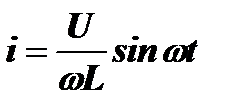 . Очевидно, что U/ωL = I,а величина ωL=XLявляется импедансом катушки. Учитывая, что sinωt=cos(ωt−π/2), получим i=I∙cos(ωt−π/2). Таким образом, напряжение и ток в катушке изменяются по гармоническому закону со сдвигом фазы на 900 (рис. 4.5).
. Очевидно, что U/ωL = I,а величина ωL=XLявляется импедансом катушки. Учитывая, что sinωt=cos(ωt−π/2), получим i=I∙cos(ωt−π/2). Таким образом, напряжение и ток в катушке изменяются по гармоническому закону со сдвигом фазы на 900 (рис. 4.5).
Заметим, что реактивное сопротивление является величиной, зависящей от времени и его мгновенное значение будет равно:
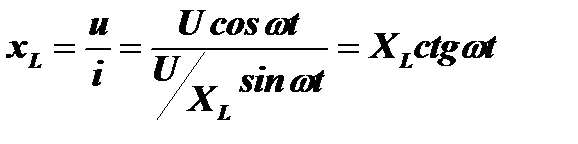 .
.
Сдвиг по фазе между током и напряжением в индуктивности объясняется следующим образом. Увеличение ЭДС источника вызывает рост ЭДС самоиндукции. В результате растет встречный вторичный ток, уменьшая («погашая») ток, вызванный в индуктивности внешним источником. Для внешнего источника это выглядит, как рост сопротивления нагрузки. Поэтому сила тока в катушке падает и достигает нуля в тот момент, когда ЭДС самоиндукции максимальна. Максимальным же ток будет в тот момент, когда эта ЭДС минимальна (рис. 4.5).
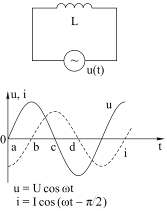
Рис. 4.5
Можно интерпретировать это явление через изменение мгновенного реактивного сопротивления.
Реактивное сопротивление действительно изменяется по закону котангенса  , ибо, когда ЭДС самоиндукции достигает максимума, а ток становится равным нулю, то xL равно бесконечности, что соответствует значениям ctgωt = np, где n – целое число.
, ибо, когда ЭДС самоиндукции достигает максимума, а ток становится равным нулю, то xL равно бесконечности, что соответствует значениям ctgωt = np, где n – целое число.
Средняя мощность . Поскольку ЭДС и сила тока сдвинуты на 90° относительно друг друга, средняя мощность, рассеиваемая в катушке, равна нулю. Действительно, в течение первого полупериода, показанного на рисунке, ЭДС положительна, а ток отрицателен. Следовательно, их произведение – среднее значение мощности – на этом участке отрицательно. В течение следующего полупериода и ЭДС и ток положительны и среднее значение мощности также положительно. Оно в точности компенсирует отрицательный вклад первой четверти. Аналогично мощность изменяется и в отрицательную часть периода. Энергия от источника поступает в катушку, где запасается ее магнитным полем, а когда поле убывает, энергия возвращается источнику. Таким образом, чистая индуктивность без потерь не потребляет и не рассеивает энергию, хотя и является сопротивлением. Следует учесть, что выражение: I=U/XL, устанавливает связь между амплитудными или эффективными значениями ЭДС и тока, но оно не выполняется для мгновенных значений этих величин из-за несовпадения их по фазе. Мгновенное сопротивление индуктивности зависит и от частоты и от времени. Поэтому пользоваться законом Ома при работе с реактивным сопротивлением следует очень осмотрительно.
Выводы:
Рассмотрев процессы, происходящие в индуктивности, мы получили ответы на вопросы, поставленные в начале раздела и можем кратко обобщить полученные результаты:
1. Причиной явлений, происходящих в индуктивности и лежащих в основе ее свойств, является появление электрического поля при изменении магнитного поля, то есть фактически возникновение единого электромагнитного поля.
2. Под действием изменяющейся электрической части электромагнитного поля в индуктивности возникает ЭДС индукции. При этом видимый источник такой ЭДС отсутствует.
Эта ЭДС вызывает ток и, связанное с этим током вторичное магнитное поле, которое противодействует изменению первоначального поля и вызванного им тока (правило Ленца), создавая эффект сопротивления без видимого физического сопротивления цепи.
Величина этого сопротивления зависит от числа витков катушки и скорости изменения тока, а, следовательно, и от частоты колебаний, ибо с ростом частоты скорость изменения тока растет.
3. ЭДС индукции опережает ток в индуктивности по фазе на 90°, поскольку только при таком соотношении фаз эта ЭДС противодействует изменениям магнитного поля катушки, реализуя, тем самым, правило Ленца. Благодаря такому сдвигу по фазе между током и напряжением индуктивность не потребляет мощности от источника. По этой же причине пользоваться законом Ома для определения сопротивления индуктивности необходимо с учетом указанного фазового сдвига.
Емкость
При рассмотрении емкости нас интересуют те же два вопроса:
- от чего зависит сопротивление емкости переменному току?
- чем определяется сдвиг по фазе между напряжением на емкости и током в емкостной цепи?
Емкость обычно реализуется в виде конденсатора, состоящего, в простейшем случае, из двух проводников (пластин), расположенных близко друг к другу. Подсоединенный к источнику постоянного напряжения U=, конденсатор быстро заряжается: положительные заряды накапливаются на одной пластине и создают на ней заряд +q, отрицательные заряды накапливаются на другой пластине и создают на ней равный по величине отрицательный заряд −q. Заряд на пластинах пропорционален напряжению источника: q = C×U=. Коэффициент пропорциональности C называется емкостью конденсатора и исчисляется в фарадах. После окончания заряда конденсатора ток через него не течет.
Если конденсатор подключить к источнику переменной ЭДС (рис. 4.6), то по цепи начнет протекать переменный ток.

Рис. 4.6
Физическая картина при этом выглядит так. В течение первого полупериода колебаний на пластинах конденсатора происходит накопление зарядов с противоположными знаками также, как это было при подключении к источнику постоянного напряжения. Когда во втором полупериоде полярность напряжения меняется, накопленные заряды перемещаются к противоположным пластинам. Таким образом, заряды все время "перекачиваются" от одной пластины к другой. И, несмотря на то, что конденсатор представляет собой физический разрыв для тока, носителями которого являются заряды, переменный ток в цепи течет непрерывно (этот ток называется током проводимости).
Ток смещения. Однако с точки зрения теории цепей необходимо, чтобы цепь для тока проводимости была замкнута. Чтобы устранить противоречие между теорией и физической картиной, вводится другой вид тока – так называемый ток смещения – позволяющий представить себе то, чего на самом деле нет – протекание тока через конденсатор. Рассмотрим, как при изучении процессов в емкостной цепи появляется ток смещения.
Диэлектрик. Сначала рассмотрим случай, когда между пластинами конденсатора находится диэлектрик. При подключении к такому конденсатору постоянной ЭДС U=, на его пластинах появляется заряд q1, создающий статическое электрическое поле E. Это поле воздействует на заряды в молекулах диэлектрика и вызывает смещение молекул с положительным зарядом в сторону отрицательно заряженной пластины, а молекул с отрицательным зарядом – в сторону положительно заряженной пластины. В результате молекулы диэлектрика перестают быть электрически нейтральными и образуют электрические диполи. Диэлектрик становится поляризованным.
Степень поляризации диэлектрика характеризуется интенсивностью поляризации P, которая для большинства диэлектриков равна:
P = N×q0×d,
где N – число диполей в единице объема диэлектрика;
q0 – заряд одного диполя;
d – расстояние между положительным и отрицательным зарядами диполя.
Опыт показывает, что интенсивность поляризации пропорциональна напряженности приложенного к диэлектрику поля E. Поляризованный диэлектрик создает в конденсаторе (наряду с уже существующим зарядом q1) дополнительный заряд q2, который связан с интенсивностью поляризации соотношением: 
где S – произвольная поверхность, охватывающая конденсатор.
Знак минус означает, что заряд q2 противоположен по знаку заряду q1. Заряд q2 часто называют связанным потому, что он не может перемещаться по цепи.
Если подключить конденсатор с диэлектриком к источнику переменной ЭДС, то заряды в подводящих проводах, возникшие от приложенного извне напряжения, будут "бегать" от пластины к пластине так, как это мы рассматривали выше. Заряды же в диэлектрике будут смещаться то в одну, то в другую сторону, меняя поляризацию диэлектрика с частотой ЭДС. Это смещение зарядов получило в физике название тока смещения. Ток смещения в диэлектрике является как бы продолжением тока проводимости в подводящих проводах и совпадает с ним по направлению и величине, хотя физического переноса зарядов сквозь диэлектрик не происходит.
Самое интересное заключается в том, что, когда диэлектрика в конденсаторе нет, и между пластинами конденсатора находится пустота (вакуум), теория сохраняет ток смещения и в пустоте, чтобы не разрывать цепь тока, соединяющую выходные контакты источника ЭДС.
Теория. Как получается ток смещения в общей теории? Рассмотрим связь зарядов q1 и q2 с образуемыми ими электрическими полями. Эта связь описывается теоремой Гаусса:  ,
,
где e – диэлектрическая проницаемость диэлектрика (если он есть).
Для нашего случая:
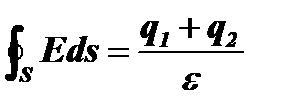
С учетом связи, которая существует между q2 и P, это равенство примет вид:

Отсюда находим:
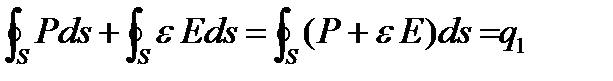
Это очень важное для электродинамики равенство. Его иногда называют обобщенной теоремой Гаусса, хотя формально она доказывается только для электростатического поля. Это равенство также называют постулатом Максвелла, поскольку оно является основным постулатом электромагнитного поля, из которого следуют все выводы теории, полностью подтвержденные опытом. Полученное равенство оказывается справедливым во всех без исключения случаях и для сколь угодно быстро изменяющихся электрических полей.
Трактовка теории. Из приведенной формулы видно, что заряд q1, создаваемый внешней ЭДС на пластинах конденсатора, уравновешивается внутри конденсатора в общем случае как зарядом, образующимся за счет смещения элементарных частиц в диэлектрике 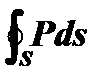 , так и зарядом, который определяется выражением
, так и зарядом, который определяется выражением 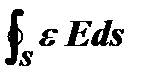 , описывающим заряд ... в пустоте (!).
, описывающим заряд ... в пустоте (!).

Теперь рассмотрим токи, протекающие в цепи конденсатора. Поскольку ток определяется количеством зарядов, прошедших через определенное сечение провода за единицу времени (то есть скоростью движения зарядов) и записывается в виде производной заряда по времени, то:
Первое слагаемое в правой части этого равенства является током смещения в диэлектрике. Его физическое существо мы рассмотрели выше. Второе слагаемое называется током смещения в пустоте. Предполагается, что оба эти тока существуют в пространстве между пластинами конденсатора и являются продолжением тока проводимости i, протекающего в подводящих проводах.
Есть ли достаточное физическое объяснение тока смещения в пустоте? Лучшим ответом может быть следующая цитата: "В отношении… тока смещения в пустоте, наглядная интерпретация при современном состоянии науки не может быть дана, так как мы еще не имеем сколько-нибудь детального представления о внутреннем строении электромагнитного поля, о тех внутренних процессах, которые в нем совершаются". (Л. Р. Нейман и К. С. Демирчан "Теоретические основы электротехники". Часть первая "Основные понятия и законы теории электромагнитного поля и теории электрических и магнитных цепей". Энергия. 1966, стр. 48).
Немного истории. Изложенные выше идеи были впервые высказаны Максвеллом и привели к созданию им теории электромагнитного поля. Согласно этим идеям при всяком изменении электрического (магнитного) поля, даже когда в нем нет частиц вещества, должно возникать связанное с ним магнитное (электрическое) поле, то есть образовываться единое электромагнитное поле. Гениальная идея Максвелла о токах смещения в пустоте позволила связать разрозненные факты и создать стройную теорию, несмотря на отсутствие понимания процессов, происходящих в пространстве, заполненном электромагнитным полем. Очевидно, что "ток в пустоте" остается не более чем искусственным приемом, не поясняющим физического существа процессов. Тем не менее, все достигнутые к настоящему времени практические результаты в области излучения и распространения электромагнитных волн, находятся в полном согласии с теорией электромагнитного поля, в основу которой положено представление об электрических токах смещения в пустоте.
Процесс в конденсаторе. Вернемся к физической картине процессов в конденсаторе, подключенном к источнику переменной ЭДС. Как отмечено выше, в течение одного полупериода переменной ЭДС на пластинах конденсатора происходит накопление зарядов противоположной полярности. По мере накопления зарядов потенциал каждой пластины становится все больше и все больше препятствует движению новых зарядов того же знака к пластине. Ток в цепи уменьшается так же, как если бы в цепи возрастало активное сопротивление. Если полупериод ЭДС существенно превышает время полного заряда конденсатора (определяемого постоянной времени цепи заряда), то конденсатор может зарядиться полностью, ток прекратится, что эквивалентно бесконечному сопротивлению (разрыву цепи). Однако если полупериод ЭДС меньше постоянной времени цепи заряда конденсатора, то полупериод другой полярности появится до полного заряда конденсатора и заряды начинают свое движение в обратную сторону. Таким образом, в цепи емкости, также как и в цепи индуктивности, сопротивление возникает без источника активных потерь.
Расчет. Рассмотрим соотношение токов и напряжений в емкостной цепи. ЭДС источника u = U×sinwt в любой момент времени равна напряжению на обкладках конденсатора uc=q/С:
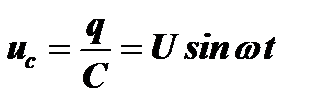

Ток в цепи будет равен:
Но coswt = sin(w t+p¤2) и, следовательно, i = I sin(wt+p¤2) то есть ток в емкостной цепи опережает напряжение на 900.
Величина wCU=U¤XC является амплитудным значением тока I, а XC=1/wC называется емкостным реактивным сопротивлением или импедансом.
Обратно пропорциональная зависимость емкостного реактивного сопротивления от емкости конденсатора и частоты переменного напряжения просто объясняется с физической точки зрения. Чем больше емкость C, тем больший заряд может накопиться в конденсаторе. Поэтому чем больше емкость, тем меньшая часть ее полного заряда будет накоплена к моменту окончания полупериода переменного напряжения частоты w и, следовательно, отталкивающее действие накопленного заряда на заряды, поступающие в цепь из источника, будет меньше. С другой стороны, чем выше частота w, тем меньше полупериод колебания, за время которого происходит накопление заряда на пластинах конденсатора; в результате этот заряд будет меньше и будет меньше препятствовать перемещению зарядов того же знака из источника к пластине.
Реактивное сопротивление емкости также, как и у индуктивности, зависит от времени: 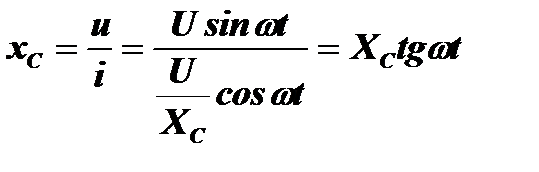 .
.
Сдвиг по фазе. Обратимся к соотношению фаз между током и напряжением в емкостной цепи при подключении ее к источнику гармонической ЭДС (рис. 4.7).

Рис. 4.7
Из физической картины заряда конденсатора видно, что максимальный ток в цепи будет протекать тогда, когда напряжение равно нулю и заряд на пластинах конденсатора отсутствует. Это значит, что ничто не препятствует движению зарядов в цепи. По мере накопления зарядов разность потенциалов на пластинах (уравновешивавшая напряжение источника) растет, а ток уменьшается. При максимальном значении этого напряжения, заряды, накопленные на пластинах, максимально препятствует движению зарядов того же знака из источника и ток становится равным нулю. Когда же напряжение проходит максимум и начинает уменьшаться, накопившиеся на пластинах заряды начинают уходить с пластин и сила тока возрастает. Этот процесс повторяется каждую половину периода, переходя с положительной полуволны на отрицательную и наоборот. В результате ток, протекающий в цепи, опережает напряжение на емкости на 90°.
Использование закона Ома. Выражение I=U¤XC, также как и в случае с индуктивностью, устанавливает связь только между амплитудными или эффективными значениями тока и ЭДС, изменяющимися по гармоническому закону. Она не пригодна для определения связи между мгновенными значениями из-за расхождения тока и напряжения по фазе. Таким образом пользоваться законом Ома при определении реактивных сопротивлений можно не всегда.
Средняя мощность. Из-за того, что напряжение и ток в емкости расходятся по фазе на 90°, потребляемая конденсатором от источника мощность в среднем равна нулю. Энергия источника переходит в энергию электрического поля конденсатора, где и запасается. Затем поле уменьшается, и энергия возвращается обратно источнику. Потерь энергии в этом процессе не происходит.
Рассмотрев процессы, происходящие в емкости, мы получили ответы на вопросы поставленные в начале раздела и можем кратко обобщить полученные результаты:
1. Явления, происходящие в емкостной цепи при подключении ее к источнику переменной ЭДС, описываются с помощью тока смещения, физически не существующего. В действительности мы имеем дело с электромагнитным полем, возникающим в емкости в этом случае.
2. Накопление потенциала на пластинах конденсатора препятствует движению зарядов в цепи конденсатора, что создает эффект сопротивления без видимого физического сопротивления в цепи.
3. Ток в цепи конденсатора опережает ЭДС источника по фазе на 90°, поскольку максимальный ток в цепи протекает в те отрезки времени, когда ЭДС источника, а, следовательно, и разность потенциалов на пластинах конденсатора, препятствующая движению зарядов, близка к нулю.
Дата добавления: 2016-04-19; просмотров: 2223;
