Корреляция между непрерывными функциями
Если интервалы между точками числовых последовательностей X и Y сделать бесконечно малыми, а число точек n - бесконечно большим, то эти последовательности преобразуются в непрерывные функции:
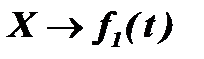
 .
.
Тогда сумма произведений чисел двух последовательностей преобразуется в интеграл от произведения этих функций на интервале от нуля до Т:
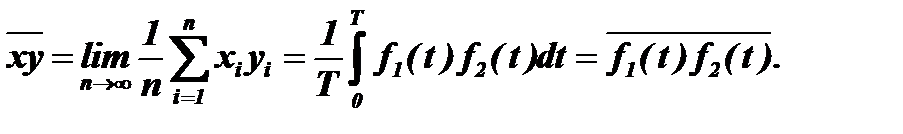
Полученное среднее значение произведения функцийf1(t) и f2(t)обозначается 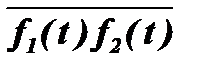 =RВ и называется их взаимной корреляцией на интервале от 0 до Т.
=RВ и называется их взаимной корреляцией на интервале от 0 до Т.
Для определения коэффициента взаимной корреляции двух функций используется такой же порядок действий, как и для дискретных последовательностей. И расчет рассмотрен для таких же двух случаев, когда 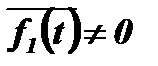 и
и 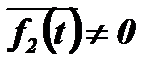 и когда
и когда  и
и 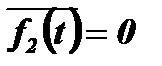 .
.
1) Находятся средние значения функций (обычно они равны нулю)
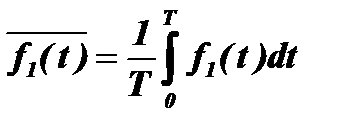
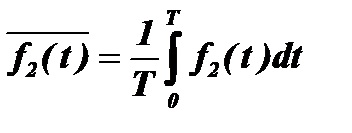
2) Находятся отклонения каждой из функций от среднего значения

 при
при 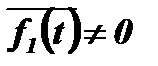 и
и 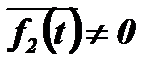 ,
,
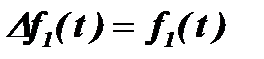
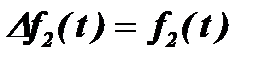 при
при  и
и 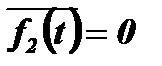 .
.
3) Находится среднее значение произведения этих отклонений
 при
при 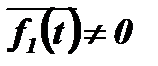 и
и 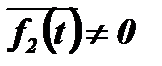 ,
,
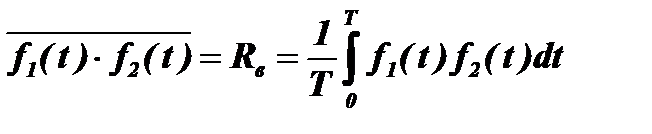 при
при 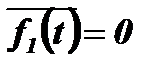 и
и 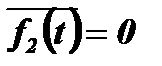 .
.
3) Находятся средние квадратичные значения этих отклонений

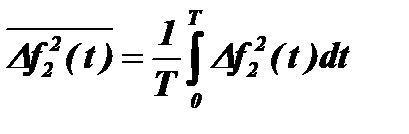 при
при  и
и 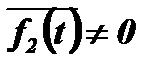 ,
,
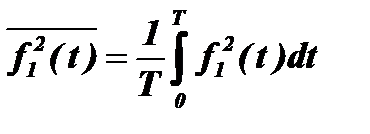
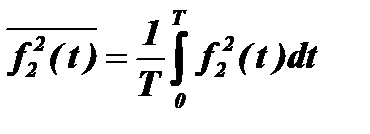 при
при 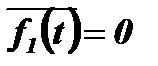 и
и 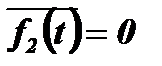 .
.
5) Находится коэффициент взаимной корреляции

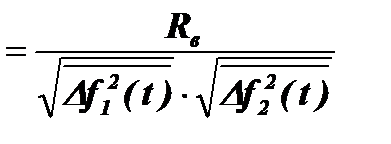 при
при 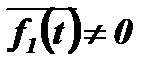 и
и 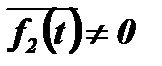 ,
,
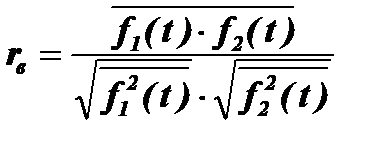
 при
при 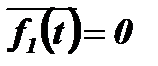 и
и  .
.
В рассмотренном случае обе функции сравниваются в одни и те же моменты времени (функции изменяются одновременно).
В общем случае нас может интересовать степень связи между двумя функциями не только тогда, когда они находятся на одном и том же интервале времени, но и при сдвиге (задержке) одной из функций относительно другой на некоторое время tз. Влияние такой задержки на степень связи между функциями хорошо иллюстрируется примером, в котором определялось влияние уровня осадков на величину урожая. Действительно, если осадки произошли весной - урожай увеличивается, если во время уборки - урожай уменьшается, если после уборки - влияние осадков на урожай отсутствует. Поэтому меняя tз можно получить различные значения корреляции. В этом случае взаимная корреляции зависит от времени задержки и становится функцией этого времени:
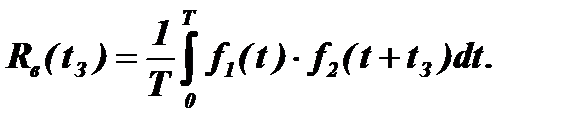
Это полное определение функции взаимной корреляции. Очевидно, что Rв (0) = Rв.
Если вместо двух разных функций дважды взять одну и ту же функциюf1(t), причём одно из её значений сместить на время tз, мы получим функцию автокорреляции (индекс "в" меняется на индекс "а"):
 .
.
Очевидно, что при tз = 0 получим:
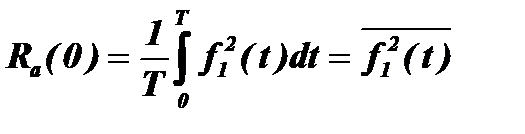 .
.
Ra(0) всегда является наибольшим значением функции автокорреляции и, например, для напряжения, описываемого функцией  , определяет среднюю мощность процесса, выделенную на сопротивлении 1 ом.
, определяет среднюю мощность процесса, выделенную на сопротивлении 1 ом.
Если произвести нормирование:
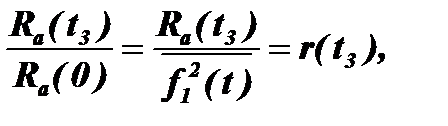
то мы получим коэффициент автокорреляции функции f1(t), зависящий от времени задержки, с пределами изменения от 0 до 1.
Дата добавления: 2016-04-19; просмотров: 1309;
