При исследовании линейных систем
Теперь можно вернуться в раздел 2.1. к формулам для коэффициентов Аn и Вn, определяющих амплитуду Сn и фазу φn n-й гармоники ряда Фурье. Мы видим, что каждый коэффициент Аn и Вn представляет собой среднее значение произведения входного сигнала Sвх(t) и гармонического колебания с частотой nW за период T, т.е. является мерой их связи. Таким образом, эти формулы представляют собой функции взаимной корреляции между сигналом Sвх(t) и синусоидальным или косинусоидальным колебанием с частотой nW. Можно сказать, что коэффициенты Аn и Вn ряда Фурье позволяют количественно определить, какую роль играет синусоида или косинусоида каждой из частот nW в составе сигнала Sвх(t), разлагаемом в тригонометрический ряд. Полученные параметры Cn и φn являются весовыми коэффициентами, которые численно характеризуют вклад каждой гармоники в этот сигнал. Когда анализируется выходной сигнал Sвых(t), то параметры CnКn и (φn+fn) являются весовыми коэффициентами каждой гармоники теперь уже на выходе системы. Тем самым определяется "количество" каждой гармоники, прошедшее через систему, то есть характеризуются фильтрующие или селектирующие свойства системы.
Интеграл Дюамеля, в свою очередь определяет степень связи между входным сигналом Sвх(t)и реакцией на него линейной системы h(t). В результате корреляционный интеграл позволяет определить, какая часть сигнала Sвх(t) содержится в выходном сигнале системы Sвых(t). Таким образом, интеграл Дюамеля также характеризует фильтрующие или селектирующие свойства системы.
Отметим различие частотных и временных методов анализа линейных систем. При преобразовании Фурье процедура представления сигнала в виде отдельных частотных составляющих (гармоник) и процедура прохождения этих составляющих через систему могут быть методически и физически выполнены раздельно. Мы можем сначала сформировать отдельные гармоники с необходимыми амплитудами и фазами и пропустить их по очереди через систему, а потом сложить полученные на выходе колебания с необходимой задержкой во времени. Так иногда и производится формирование сложных сигналов. При использовании интеграла Дюамеля представление сигнала в виде отдельных элементарных составляющих и прохождение этих составляющих через систему выполняется в виде единой процедуры, происходящей в текущем времени.
Если тот или иной корреляционный интеграл равен нулю, то это значит, что рассматриваемые функции не имеют между собой никакой связи, не коррелированны. Однако некоррелированность двух функций не всегда означает их полную независимость. Так, корреляционный интеграл от произведения sin ωt и cos ωt на интервале T
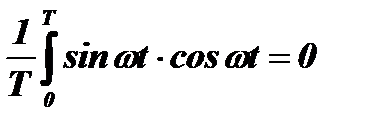 ,
,
и, по определению, эти функции не коррелированны, но, очевидно, что они зависимы. Такие функции называются ортогональными. К их свойствам мы вернемся в дальнейшем.
Дата добавления: 2016-04-19; просмотров: 920;
