Коэффициент корреляции
Мерой связи двух последовательностей чисел мы определили среднее значение произведений совпадающих пар чисел 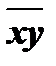 . При ненулевом среднем значении каждой последовательности в качестве чисел использовались их отклонения от среднего значения своей последовательности
. При ненулевом среднем значении каждой последовательности в качестве чисел использовались их отклонения от среднего значения своей последовательности 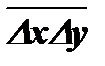 . Однако при таком определении разные пары последовательностей, описывающие совершенно различные явления, но имеющие одинаковые степени связи, могут иметь разные средние значения. Поэтому использование величины
. Однако при таком определении разные пары последовательностей, описывающие совершенно различные явления, но имеющие одинаковые степени связи, могут иметь разные средние значения. Поэтому использование величины 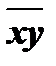 (
( 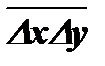 ) на практике неудобно, поскольку затрудняет сравнение различных пар последовательностей по степени связи. Чтобы сделать оценку связи единообразной, вместо величины
) на практике неудобно, поскольку затрудняет сравнение различных пар последовательностей по степени связи. Чтобы сделать оценку связи единообразной, вместо величины  (
( 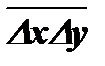 ) используется нормированная величина r, которая называется коэффициентом корреляции. Для произведения
) используется нормированная величина r, которая называется коэффициентом корреляции. Для произведения  коэффициент корреляции равен:
коэффициент корреляции равен:
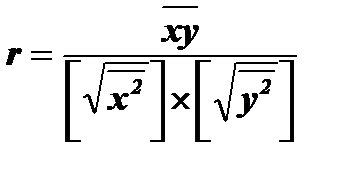 , где
, где 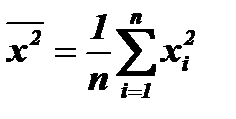 и
и 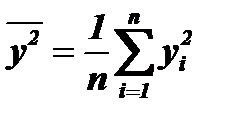 ,
,
где 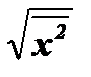 и
и 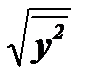 - средние квадратичные величины последовательностей X и Y. Благодаря такой нормировке, коэффициент корреляции, в отличие от среднего значения
- средние квадратичные величины последовательностей X и Y. Благодаря такой нормировке, коэффициент корреляции, в отличие от среднего значения  , изменяется только в пределах от +1 до -1, т.е.
, изменяется только в пределах от +1 до -1, т.е. 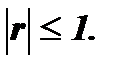
Таким образом, в самом общем случае для нахождения коэффициента корреляции двух дискретных последовательностей X и Y необходимо выполнить следующие действия (расчет рассмотрен для двух случаев: когда 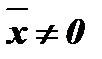 и
и 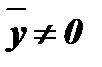 и когда
и когда 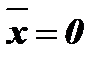 и
и 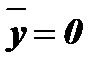 ):
):
1) Найти среднее значение каждой из этих последовательностей:


2) Найти отклонения каждого значения каждой из последовательностей от среднего значения:
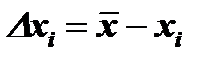 ,
, 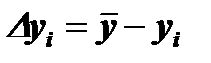 при
при 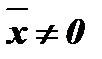 и
и 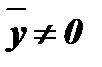 .
.
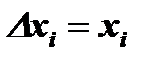 ,
, 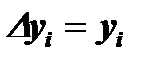 при
при 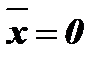 и
и 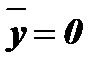 .
.
3) Найти среднее значений произведения этих отклонений:
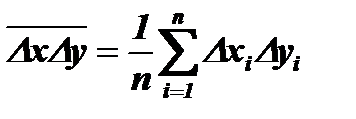 при
при 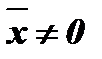 и
и 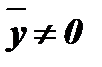 .
.
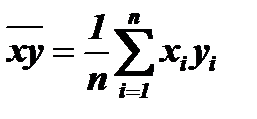 при
при  и
и 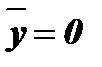 .
.
4) Найти средние квадратичные значения этих отклонений:
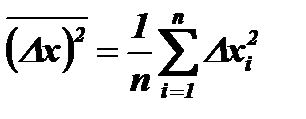 и
и  при
при 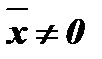 и
и 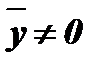 .
.
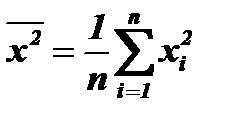 и
и 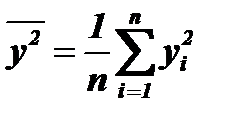 при
при 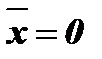 и
и 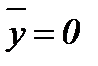 .
.
5) Найти коэффициент корреляции:
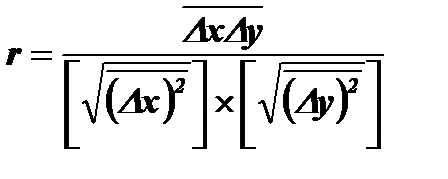 при
при 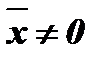 и
и 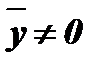 .
.
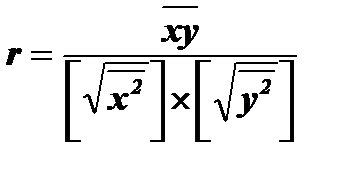 при
при 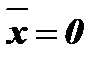 и
и 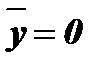 .
.
Дата добавления: 2016-04-19; просмотров: 796;
