Классификация радиотехнических систем

Фундаментальные понятия используются при построении самых различных радиотехнических систем. Поэтому рассмотрим, как классифицируются такие системы, какие они имеют возможности и особенности.

Задачей любой радиотехнической системы является формирование или преобразование электрических сигналов. Однако виды преобразований, которые реализуются в тех или иных радиотехнических системах, могут быть весьма различными и определяются структурой системы. А по своей структуре все радиотехнические системы делятся на несколько крупных классов. Рассмотрим, как производится классификация этих систем.

Любая передача или преобразование сигналов в радиотехнической системе физически осуществляется при движении электрических зарядов или электромагнитных полей. Универсальным математическим аппаратом, описывающим любое движение, являются дифференциальные уравнения. Радиотехнические системы также описываются дифференциальными уравнениями и делятся на классы в зависимости от типа уравнений, которые описывают их поведение. Поэтому название классов радиотехнических систем традиционно связывают с названиями типов дифференциальных уравнений, которые описывают работу этих систем.

В общем виде дифференциальное уравнение, например, для тока i, протекающего в системе, имеет вид:

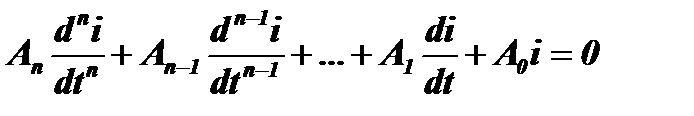
Решение этого уравнения позволяет получить зависимость тока i от времени t. Поэтому ток i называется зависимой переменной, в отличие от времени t, которое является переменной независимой. Коэффициенты при производных разного порядка А_n, А_n-1, … А₀ называются параметрами системы. Производная самого высокого порядка определяет число степеней свободы системы.

Если система автономна и не связана с внешними источниками энергии, то правая часть ее дифференциального уравнения равна нулю. Такое дифференциальное уравнение называется однородным. Если система соединена с внешним источником энергии, то его воздействие на систему записывается в правой части уравнения. Такое уравнение называется неоднородным и имеет вид:

.

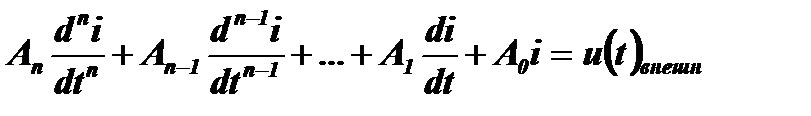В рассмотренном примере параметры системы должны иметь размерность сопротивлений.

Поведение всей системы определяется свойствами параметров системы, являющихся коэффициентами уравнения. Параметры могут быть постоянными величинами и переменными величинами. Переменные параметры могут меняться во времени, то есть меняться при изменении независимой переменной, или могут меняться при изменении зависимой переменной; такой переменной в нашем примере является ток. Параметры системы могут также меняться при одновременном изменении обеих переменных.

В результате, в зависимости от свойств параметров, образуются четыре класса радиотехнических систем и описывающих их дифференциальных уравнений (рис. 1.4).

1. Дифференциальные уравнения с постоянными параметрами описывают стационарные линейные системы.

2. Дифференциальные уравнения с параметрами, зависящими только от времени описывают линейные параметрические системы.

3. Дифференциальные уравнения с параметрами, зависящими только от тока (или другой зависимой переменной), но не зависящими от времени, описывают нелинейные системы.

4. Дифференциальные уравнения с параметрами, зависящими и от тока и от времени, описывают нелинейные параметрические системы.

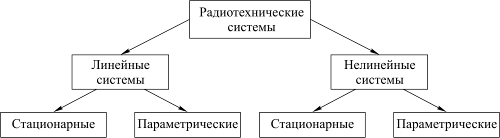
Рис. 1.4

Первые и третий классы охватывают подавляющее большинство существующих радиотехнических систем. Второй класс систем распространен в меньшей степени. Четвертый класс систем пока не получил своего развития. Дело в том, что точные аналитические решения получены далеко не для всех, указанных выше, типов дифференциальных уравнений. С этим связана различная степень освоения и развития разных классов радиотехнических систем.

Рассмотрим наиболее характерные особенности указанных выше классов систем.

Линейные системы с постоянными параметрами или стационарные линейные системы, описываются линейными уравнениями с постоянными коэффициентами. Это самый простой тип уравнений, теория которых детально разработана и для решения которых существуют общие методы. В линейных системах можно применять принцип суперпозиции. Важно отметить, что сама применимость принципа суперпозиции служит определением линейной системы.

Типичным примером линейной системы с постоянными параметрами является обычный, например последовательный, колебательный контур с постоянными параметрами L,С и R. Изменение заряда q, связанного с током в контуре соотношением 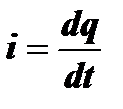описывается дифференциальным уравнением второго порядка:

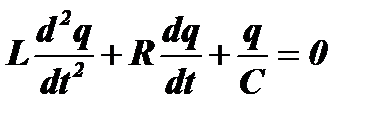или .

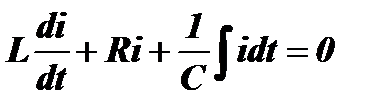При внешнем воздействии на контур гармонического колебания с некоторой частотой w, его дифференциальное уравнение становится неоднородным:

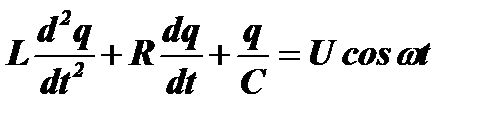
Главной задачей стационарных линейных систем в радиотехнике является выделение некоторого диапазона частот, то есть выполнение функций частотной селекции и частотной фильтрации; выделение некоторого временного интервала, то есть выполнение функций временной селекции, а также линейное усиление колебаний.

Главная особенность стационарных линейных цепей, отличающая их от цепей с переменными параметрами и нелинейных цепей – отсутствие в составе выходного спектра новых частот по сравнению с составом спектра на входе.

Линейные системы с переменными параметрами, которые называются также параметрическими или нестационарными линейными системами, описываются линейными уравнениями с переменными коэффициентами. Коэффициенты уравнения зависят от независимой переменной, которой, как правило, является время. С физической точки зрения это означает, что параметры системы так или иначе изменяются во времени. Теория, позволяющая получать решения этих уравнений, более сложна и менее разработана, чем теория линейных систем. Поэтому в литературе иногда явления, описываемые линейными уравнениями с переменными коэффициентами, относят к "нелинейной" радиотехнике. Типичным примером системы с переменным параметром является колебательный контур с емкостью, изменяющейся во времени. Его однородное дифференциальное уравнение, описывающее изменение заряда, имеет вид:

.

Решение этого уравнения найдено только для частного случая, когда контур не имеет потерь (R=0) и изменяется по гармоническому закону с частотой ω_п и относительной глубиной m:

Это уравнение носит имя Матье. Оно играет большую роль при проектировании и расчете параметрических систем.

К параметрическим линейным системам также применим принцип суперпозиции. В этом они похожи на линейные системы с постоянными параметрами. Однако параметры нестационарных систем непрерывно изменяются, и поэтому, строго говоря, в них допустима суперпозиция действующих сил только для малого интервала времени, на котором изменениями параметров системы можно пренебречь.

В спектре выходных колебаний параметрических линейных систем возможно появление новых частот, отсутствующих во входном спектре. Это сближает их с нелинейными системами, но и здесь есть одно важное отличие: в параметрических линейных системах могут создаваться различные комбинационные колебания из частот, действующих на входе, но невозможно создание гармоник, то есть частот, кратных по отношению к входной частоте. Поэтому в выходном спектре параметрической системы не может быть частот, значения которых превышают сумму частот всех колебаний, действующих на входе системы.

Параметрические системы могут выполнять функции как линейных цепей (усиление колебаний), так и нелинейных цепей (детектирование, генерирование).

Стационарные нелинейные системы описываются нелинейными дифференциальными уравнениями, коэффициенты которых зависят от зависимой переменной (например, тока или напряжения), а также от её производных. Это весьма трудный для решения тип дифференциальных уравнений. Прямых общих методов решения таких уравнений пока нет. Эти уравнения обычно решаются приближенными методами, позволяющими получить решения с различной степенью погрешности.

Типичным примером является нелинейное уравнение автогенератора:

,

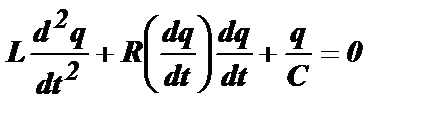у которого сопротивление колебательного контура 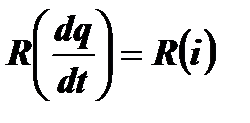зависит от тока, протекающего в системе. Можно получить отрицательное значение величины R(i). Этом случае система будет не поглощать энергию, а, наоборот, вырабатывать, то есть, генерировать ее. Нелинейные системы выполняют в радиотехнике целый ряд чрезвычайно важных функций: генерирование электрических колебаний и деление частоты, выпрямление и детектирование, модуляция и преобразование частоты. В выходном спектре таких систем всегда есть новые частоты, отсутствующие в спектре входного сигнала.

Нестационарные нелинейные системы не получили своего развития из-за сложности реализации и практически полного отсутствия необходимой теоретической базы. Тем не менее, необходимо отметить, что этот класс систем должен обладать значительно более широкими возможности по различному преобразованию сигналов, чем системы других классов, за счет более гибкого, «двумерного» управления параметрами, как во времени, так и по зависимому от системы параметру (току, напряжению, магнитному полю и т.п.). Можно предполагать, что у этого класса систем большое будущее.

При современном развитии вычислительной техники стало доступным моделирование сложных радиотехнических систем, описываемых дифференциальными уравнениями, не имеющими сегодня теоретического решения. Однако математическое моделирование позволяет получить результаты для относительно частных случаев, в то время как решение дифференциальных уравнений позволяет, во-первых, создать общую картину процессов, происходящих в системе и понять направление развития этих процессов, а, во-вторых, разработать методы количественного исследования радиотехнических устройств, необходимые, в конечном счёте, для их математического моделирования.

Расчёт конкретной радиотехнической системы всегда является конечным этапом любой исследовательской и прикладной работы. Вот почему так важно знать и помнить, какие математические методы исследования пригодны для того или иного класса систем. В тоже время, чем сложнее система, тем важнее понимать физическую сущность происходящих в ней процессов. Ибо, только понимая суть процессов, можно оценить правильность выбора теоретического подхода и правильность результатов количественного расчёта.

Корреляция