Методы исследования линейных систем
В радиотехнике часто возникает необходимость определения сигнала на выходе линейной системы, когда известны и сигнал на входе и коэффициент передачи самой системы. Обычно для решения этой задачи входной сигнал делится на однотипные элементарные составляющие либо во временной области, либо в области частот. Далее используется принцип суперпозиции: рассматривается прохождение каждой элементарной составляющей сигнала через линейную систему (с учетом коэффициента передачи системы для этой элементарной составляющей), а затем полученные результаты суммируются, образуя выходной сигнал.
Существует ли какое-нибудь правило, в соответствии с которым входной сигнал делится на элементарные составляющие и происходит выбор этих составляющих? Попытаемся ответить на этот вопрос. Обратимся сначала к частотной области.
Если входной сигнал отвечает условию S(t) = S(t+T), то есть является периодическим с периодом Т, то такой сигнал, как известно, можно представить в виде суммы элементарных гармонических колебаний (гармоник), образующих ряд Фурье:
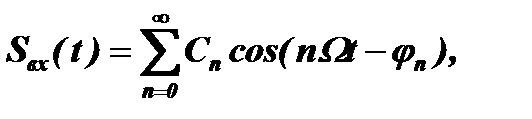
здесь: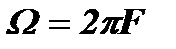 
, 
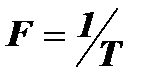, а коэффициенты 
и 
,
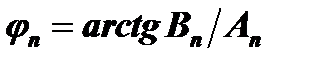где в свою очередь:
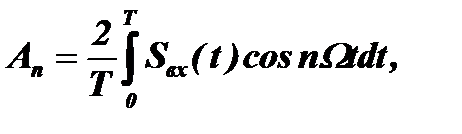
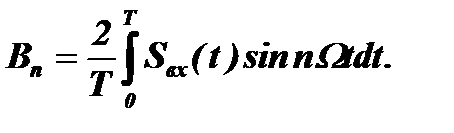
Чтобы получить сигнал на выходе системы Sвых(t) необходимо амплитуду каждой гармоники Cn умножить на коэффициент передачи системы по амплитуде на n-ой частоте Кn и учесть коэффициент передачи системы по фазе на этой частоте fn:
Таким образом коэффициенты An и Вn позволяют определить амплитуду Cnи фазу jn каждой гармоники ряда, как на входе, так и на выходе системы.
Для нас важно понять структуру формул, с помощью которых определяются коэффициенты An и Вn. Физический смысл этой структуры пока не ясен. Почему эти формулы выглядят именно так? Какой смысл в перемножении входного сигнала на гармоническое колебание n-ой частоты? И зачем это произведение затем интегрируется?
К ответам на эти вопросы мы вернемся позже, а пока рассмотрим, случай, когда прохождение входного сигнала через линейную систему рассматривается во времени, а входной сигнал делится на элементарные составляющие во временной области. Это удобно, поскольку любой входной сигнал может быть представлен, как последовательность коротких импульсов.
| Рис. 2.2 |
| Рис. 2.1 |
Теперь подадим на вход сиcтемы сигнал в виде последовательности импульсов x(m) в моменты времени m. На рисунке 2.2 выходной сигнал в момент времени 0 равен y(0), причем
y(0)=h(0) x(0)
В дискретный момент времени m=1 выходной сигнал равен h(0)x(1) [влияние текущего входного сигнала x(1)] плюс h(1) x(0) (запаздывающее влияние входного сигнала, поданного в момент m=0).
Следовательно,
y(1)=h(1)x(0)+h(0)x(1)
Таким образом, последующие выходные сигналы запишутся так:
y(2)=h(2)x(0)+h(1)x(1) +h(0)x(2)
y(3)=h(3)x(0)+h(2)x(1) +h(1)x(2) +h(0)x(3)
: ()
:
y(n)=h(n)x(0)+h(n-1)x(1) +…….. +h(0)x(n)
Если система линейна, выходной сигнал можно записать как линейную сумму влияния предыдущих входных сигналов. Выходной сигнал линейной системы первого порядка описывается этим уравнением.
Из приведенных выражений, видно, что выходной сигнал получается умножением входной последовательности на соответствующие точки обращенной во времени функции импульсной характеристики. Можно записать полученное уравнение и в таком виде:
y(n)=h(0)x(n)+h(1)x(n-1) +…….. +h(n)x(0)
и рассматривать выходной сигнал, как произведение соответствующих пар точек в функции импульсной характеристики и обращенной во времени входной последовательности. Следовательно, сверточная сумма эквивалентна взаимной корреляции одной последовательности и обращенной во времени другой.
Приведенные выше уравнения можно записать компактно:
y(n)=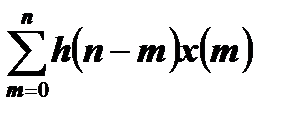 
и
y(n)=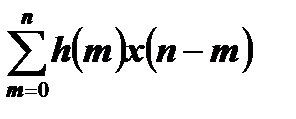 
Данные функции называются сверточными суммами входных сигналов импульсной характеристикой, а выходной сигнал называтся сверткой входного сигнала с импульсной характеристикой системы.
Эти уравнения можно распространить на сигналы бесконечной длительности, записав их следующим образом:
y(n)=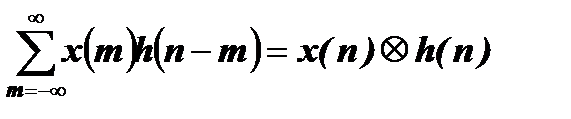 
y(n)=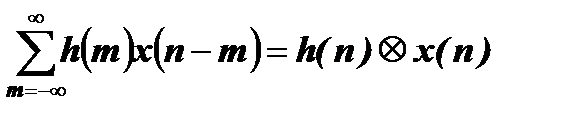 
В приведенных уравнениях символ 
обозначает операцию свертки.
Если входной сигнал состоит из непрерывной последовательности импульсов, приведенные выше суммы можно заменить интегралами, например, первая сумма приводится к виду:
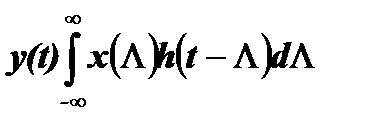
Этот интеграл называется интегралом свертки или интегралом Дюамеля.
Таким образом, и корреляционная операция свертки требует, чтобы одна из последовательностей умножалась на (обращенную во времени) вторую последовательность и полученные произведения суммировались или интегрировались. Свертка соответствует взаимной корреляции одной последовательности с обращенной во времени второй.
Она получена суммированием откликов системы на отдельные элементарные воздействия во временной области, то есть с помощью принципа суперпозиции, и с этой точки зрения интеграл Дюамеля аналогичен интегралу Фурье.
Представив выходной сигнал в виде набора элементарных составляющих во временной области, мы видим, что этот сигнал снова имеет вид интеграла от произведения входного сигнала и отклика системы на элементарное воздействие. Закономерность, отмеченная нами при частотном анализе линейной системы, повторилась и при анализе временном.
Как мы отметили выше, основным назначением преобразований Фурье и Дюамеля является определение сигнала на выходе системы по известному входному сигналу. Однако нас в данном случае интересует не решение этой задачи – она рассматривается в других курсах. Здесь нас интересует ответ на другой вопрос – почему формулы для определения сигнала при разных видах преобразований имеют одинаковую структуру: интеграл от произведения двух функций?
Чтобы сократить путь к ответу, заметим, что структура этих формул совпадает со структурой корреляционного интеграла, который в общем случае для двух функций времени f1(t) и f2(t) имеет вид:
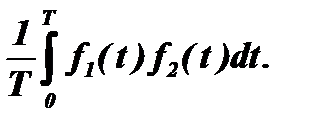
Тогда ответ на поставленный вопрос целесообразно поискать в недрах корреляционного анализа. Попробуем сделать это.
Дата добавления: 2016-04-19; просмотров: 1010;