Корреляционный анализ. В первой половине ХХ века инженеры, занимавшиеся разработкой радиоаппаратуры, применяли в расчетах однозначные соотношения между параметрами приборов и

В первой половине ХХ века инженеры, занимавшиеся разработкой радиоаппаратуры, применяли в расчетах однозначные соотношения между параметрами приборов и устройств, которые задавались либо формулами (например, значение резонансной частоты), либо графиками (например, петля гистерезиса). Не было никакой неясности относительно характера связи между величинами - они были либо независимы, либо находились в известной функциональной зависимости.

Однако со временем в радиотехнике стала постепенно возрастать роль случайных шумовых процессов и их описание потребовало привлечения статистических методов. Одним из таких методов явился корреляционный анализ, предложенный еще в 1890г. английским психологом и антропологом Гальтоном (двоюродным братом Чарльза Дарвина) под названием "исчисление выравнивания" для статистической обработки результатов исследований. Современное название методу дал английский математик Тейлор в 1920г.

Существо корреляционного анализа сводится к следующему. Положим, что на некотором наблюдаемом интервале времени или на отрезке пространства существуют две (или более) последовательности дискретных величин, между которыми явная функциональная зависимость отсутствует. Вместо последовательности дискретных величин могут быть взяты непрерывные функции. Корреляционный анализ позволяет определить, существует ли какая-либо связь между этими последовательностями или функциями. Если связи нет, то величины являются независимыми. Если связь есть, величины называются коррелированными, а величина этой связи может быть определена количественно, в виде числа.

Чтобы понять суть корреляционного анализа, рассмотрим простой пример. Возьмём две последовательности чисел Х и Y:

x₁, x₂, x₃, ……… x_i, … x_n

y₁, y₂, y₃, ……… y_i, … y_n .

Эти последовательности могут описывать разные явления. Возьмем далекий от радиотехники пример. Предположим, что первая последовательность показывает уровень осадков по годам, а вторая - величину урожая в эти годы (Рис. 2.2).

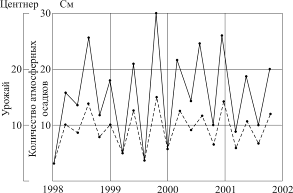
Рис. 2.2

Как определить степень связи этих последовательностей или изображающих их графиков?

Гальтон предложил следующую несложную операцию: числа первой и второй последовательностей в совпадающие моменты времени попарно перемножаются, образуя произведения вида x_iy_i. Затем эти произведения суммируются и полученная сумма делится на число просуммированных пар, т.е. находится среднее значение произведений ху на рассматриваемом отрезке времени:

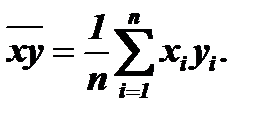
Это среднее значение Гальтон предложил использовать для определения степени связи между рассматриваемыми последовательностями. Почему он решил, что это выражение наилучшим образом отражает такую связь?

Чтобы ответить на этот вопрос необходимо установить, какой знак получает произведение x_iy_i при разном сочетании знаков у сомножителей.

Однако прежде следует определить, откуда должен отсчитываться знак каждого сомножителя. Ведь если посмотреть на рис. 2.2, то станет очевидно, что на этом рисунке отсчет всех чисел x_i и y_i производится от нуля (нуля осадков или нуля урожая), а эти числа всегда имеют положительный знак и, соответственно, все произведения будут положительными.

Гальтон предложил отсчитывать отклонение чисел x_i и y_i не от абсолютного значения (которое может быть совершенно произвольным в различных случаях, как на рис. 2.2), а от среднего значения соответствующей последовательности:

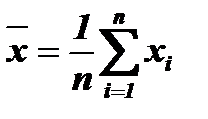и

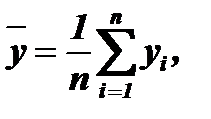
Тогда для определения степени связи между двумя последовательностями необходимо найти среднее значение произведения не самих чисел каждой последовательности x_i и y_i, а их отклонений от своего среднего значения 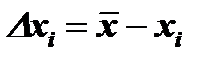и 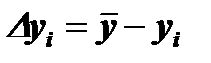. Тогда формула Гальтона примет окончательный вид:

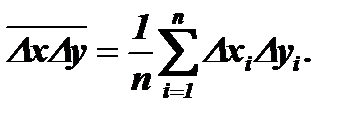
Отметим, что средние значения большинства электрических и радиотехнических процессов обычно равны нулю (постоянная составляющая, не несущая информации, как правило, устраняется включением конденсатора или трансформатора). В этих случаях 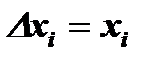, а .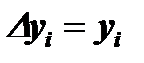

Теперь вернемся к знаку произведения x_iy_i.

Есл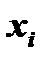и и 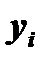- оба положительны, или оба отрицательны, то их произведение будет положительно. Произведение будет отрицательным только в том случае, когда величины 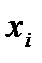и 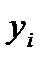имеют разные знаки. Таким образом, благодаря этой особенности операции перемножения, одинаковое отклонение величин, независимо от их знака, дает положительный знак произведению x_iy_i, а отклонение этих величин с разными знаками приводит к отрицательному знаку произведения.

Это означает, что при достаточно большом числе совпадающих по знаку пар величин x_i и y_i величина 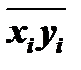(или ) будет положительна. И чем больше таких пар, тем больше будет величина 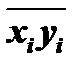. В этом случае последовательности X и Y называют зависимыми и ковариантными.

Если же в последовательности большое число пар имеет разные знаки, то величина 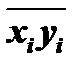(или 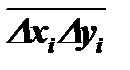) будет отрицательной и также будет расти при увеличении числа таких пар. В этом случае последовательности X и Y тоже будут зависимые, но контравариантные. Как видно, их зависимость будет отрицательной.

А если число совпадающих по знаку пар x_i и y_i будет примерно равно числу пар с разными знаками, то положительные произведения скомпенсируют отрицательные и величина 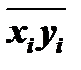(или 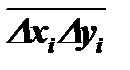) будет равна нулю или близка к нему. Это означает, что последовательности X и Y независимы и связи между ними почти нет или, возможно, совсем нет.

Таким образом, корреляционный анализ двух дискретных последовательностей на некотором временном интервале выполняется с помощью двух процедур:

1) Сравнение знаков у элементов двух последовательностей, существующих в один и тот же момент времени. При выполнении этой процедуры элементы последовательностей как бы "узнают" степень совпадения (или несовпадения) знаков друг друга. Процедура выполняется операцией перемножения.

2) накоплению (суммированию) результатов этой "проверки". Процедура выполняется операцией сложения.

Является ли этот метод наилучшим для определения меры связи между двумя последовательностями каких-либо чисел или величин? Сегодня мы отвечаем на этот вопрос положительно, поскольку этот метод широко применяется во многих областях науки и практики, в том числе и в радиотехнике. К конкретным примерам мы обратимся позднее.