Применение корреляционной обработки для разделения информационных каналов

С недавнего времени корреляционная обработкастала использоваться в радиотелефонии для организации работы нескольких телефонных каналов в одной и той же полосе частот без взаимных помех. Это позволяет преодолеть «тесноту» в эфире и расширить возможности систем связи. Рассмотрим, как работает такая система, получившая название МДКР – Многостанционный Доступ с Кодовым Разделением каналов (английская аббревиатура: CDMA - Code Division Multiple Access).

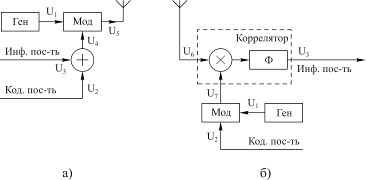
Рис. 2.4

Структурная схема передатчика системы показана на рис. 2.4,а, а временные диаграммы сигналов в отдельных узлах передатчика – на рис. 2.5,а.

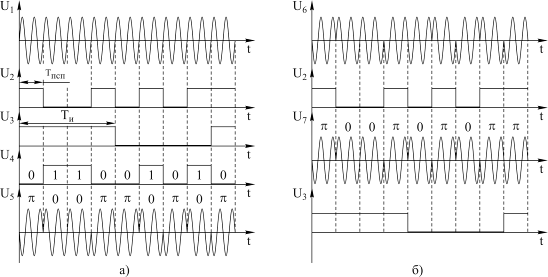
Рис. 2.5

Высокочастотный генератор формирует несущее колебание U₁ на частоте f_нес. Для разделения абонентских каналов используется кодовая импульсная последовательность U₂. Длительность импульсов этой последовательности T_k и тактовая частота F_k. Информация от абонента поступает в виде цифровой импульсной последовательности U₃. Тактовая частота этой последовательности F_и и длительность импульсов T_и. В системе соблюдается условие: Т_и=N×T_k, где N >>1, то есть импульс кодовой последовательности U₂ в N раз короче импульса информационной последовательности U₃. Импульсные последовательности U₂ и U₃ складываются в сумматоре «по модулю два» и образуют импульсную последовательность U₄. При их сложении «по модулю два» спектр информационной последовательности расширяется в N раз до ширины спектра кодовой последовательности. Последовательность U₄ модулирует по фазе (0, p) колебание U₁ высокочастотного генератора. Это колебание излучается в пространство. Двоичной единице соответствует начальная фаза несущего колебания равная 0, двоичному нулю – начальная фаза несущего колебания равная p. При расширении спектра в N раз уменьшается спектральная плотность мощности сигнала передатчика. В результате полученный сигнал имеет высокую энергетическую скрытность и высокую криптостостойкость, так как период повторения кодовой последовательности может быть очень длинным, а определить порядок чередования кодирующих импульсов, не зная алгоритм формирования кодовой последовательности, практически невозможно.

Структурная схема приемника системы показана на рис. 2.4,б, а временные диаграммы работы в приемнике – на рис. 2.5,б. Принятый широкополосный сигнал U₆ подается в коррелятор, где в качестве опорного сигнала используется модулированное высокочастотное колебание U₇,формируемое из высокочастотного колебания U₁ с помощью модуляции по фазе (0,p) кодовой последовательностью импульсов U₂. В результате корреляционной обработки на выходе коррелятора остается только информационная последовательность импульсов U₃.

Для разделения нескольких абонентов, работающих в общей полосе частот, можно использовать различные типы кодовых последовательностей. Однако для нас важно, чтобы эти последовательности обладали хорошими автокорреляционными и взаимокорреляционными свойствами. Когда корреляционный приемник сравнивает принимаемую кодовую последовательность с опорной кодовой последовательностью и обнаруживает корреляцию между ними, он переходит в режим приёма информации, устанавливает синхронизацию и начинает операцию декодирования полезной информации. Любые частичные корреляции с кодовыми последовательностями других абонентов могут привести к нарушению работы приёмника. Поэтому слова “хорошие автокорреляционные и взаимокорреляционные свойства” означают, что кодовые последовательности, используемые в системе связи, должны иметь коэффициент автокорреляции равный 1 и коэффициент взаимной корреляции равный 0. Такими свойствами обладают ортогональные функции. С математи­ческой точки зрения ортогональность функций означает, что интеграл от произведения двух любых, но разных функций ансамбля (функция взаимной корреляции) всегда будет равен нулю, а функция автокорреляции любой функции ансамбля будет равна единице. Такими функциями, например, являются гармоники ряда Фурье. Пример, показывающий ортогональность этих функций, приведен в конце раздела 2.5. Поэтому если в системе связи для кодирования использовать ортогональные последовательности, то коррелятор каждого приёмника выделит только строго определённую последовательность. Выходное напряжение коррелятора при приеме кодовых последовательностей соседних каналов будет нулевым.

В качестве ортогональных сигналов для создания кодовых последовательностей в цифровых системах связи наиболее часто используется ансамбль функций Уолша, имеющих прямоугольную форму и кратко обозначаемых символом Wal. На рис.2.6 показано несколько первых функций ряда Уолша.

Рис. 2.6

Прямоугольная форма функций Уолша наилучшим образом сочетается с передачей цифровых сигналов.

Последовательности Уолша определяются строками или столбцами единичных матриц, которые называются матрицами Адамара.

На рис. 2.6 показана матрица Адамара четвёртого порядка и соответствующие ей первые четыре функции Уолша. Связь строк матрицы и функций Уолша здесь очевидна. Перемножая любую пару функций на заданном отрезке, мы всегда получим равное число положительных и отрицательных единиц, которые при суммировании на этом отрезке дадут нуль, реализуя, тем самым, некоррелированность функций.

Количество функции Уолша, используемых в системе, определяет число независимых каналов, которое может содержать система. С этой точки зрения выгодно использовать функции Уолша как можно более высокого порядка. С другой стороны, чем выше порядок функции Уолша, тем короче единичный символ последовательности и тем шире должна быть полоса частот системы для неискаженного пропускания данной последовательности. Поэтому приходится искать компромисс между числом каналов и полосой пропускания системы. В системах сотовой связи обычно используются функции Уолша шестьдесят четвёртого порядка.

В этом случае каждый информационный символ складывается в передатчике «по модулю два» с присвоенной этому каналу функцией Уолша, имеющей 64 элементарных символа. С информационным нулем складывается сама функция Уолша, а с информационной единицей − инверсная (перевернутая по знаку) функция Уолша.

Спектр излучаемого сигнала при этом расширяется в 64 раза. Если коррелятор приемника "узнает" кодовую последовательность "своего" канала, то сумма произведений функций Уолша даст единицу и принятый информационный символ сохраняется в приемнике. А если коррелятор приемника "не узнает" кодовую последовательность, то сумма произведений функций Уолша даст ноль, в результате чего принятый информационный символ удаляется из приемника. Очищенная от кода информационная последовательность поступает на выход приемника.

Таким образом, и в этом случае корреляционный анализ позволяет "узнать" свой сигнал – свою кодовую последовательность – и выделить ее из смеси многих других сигналов, сравнивая принятую кодовую последовательность с опорной.