Постоянными параметрами (компенсационный резонанс).

Мы рассмотрели поведение индуктивности и емкости в цепи переменного тока. Теперь соединим их в единую LC цепь (рис. 4.8).

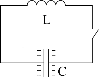
Рис. 4.8

Пренебрежем сначала потерями в этой цепи и проведем простой эксперимент: зарядим конденсатор от какого-либо внешнего источника до величины q, а потом уберем внешний источник и, замкнув выключатель, начнем разряжать конденсатор через индуктивность, вызвав тем самым в цепи ток i. Отметим, что для такого эксперимента источником энергии может быть только емкость, поскольку индуктивность не может запасти и хранить энергию. Когда заряд конденсатора станет равен нулю, ток в индуктивности достигнет максимального значения, а индукция магнитного поля будет максимальна. Эта индукция вызовет ЭДС самоиндукции, которая начнет заряжать конденсатор. Ток постепенно будет уменьшаться, а заряд на пластинах конденсатора - увеличиваться. Когда ток уменьшиться до нуля, заряд конденсатора снова достигнет максимума, но знаки заряда на обкладках поменяются местами, относительно предыдущего значения. Процесс будет повторяться и максимальный заряд конденсатора будет чередоваться с максимумом тока в индуктивности. Таким образом, в контуре возникнут электромагнитные колебания. Они называются свободными колебаниями. Если в контуре нет потерь (R=0), то эти колебания будут незатухающими.

Четыре стадии процесса "перекачки" энергии между емкостью к индуктивностью, соответствующие четырем четвертям периода колебаний, показаны на рисунке 4.9.

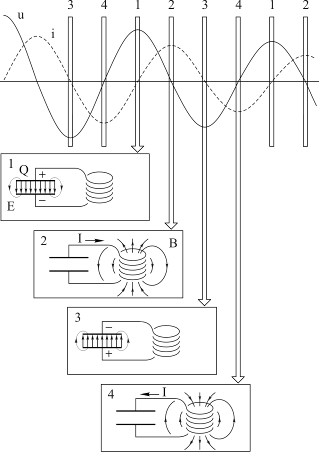
Рис. 4.9

Таким образом, индуктивность и емкость дополняют друг друга, создавая единую колебательную систему. Это - уникальная пара и других подобных пар электрических элементов в природе, по-видимому, не существует.

Процессы в контуре без потерь во временной области. Поскольку в каждый момент времени разность потенциалов (напряжение) на обкладках конденсатора уравновешивается ЭДС самоиндукции: u_C = e, то можно записать 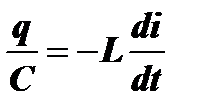или

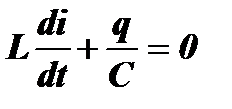. (1)

Форма колебаний, возникающих в контуре, находится из решения этого дифференциального уравнения. Учитывая, что 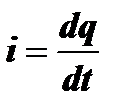и, следовательно, 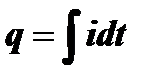, можем привести (1) к уравнению для тока в контуре: 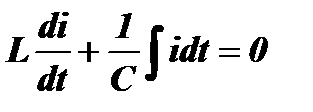или, после дифференцирования по t: .

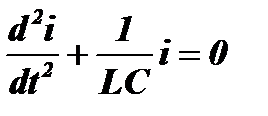Вид этого уравнения показывает, что его решением должна быть функция, значение которой в любой момент времени (с точностью до постоянного множителя 1/LC) равно ее второй производной. Обозначим для сокращения записи: 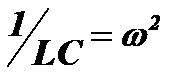и представим уравнение в виде: .

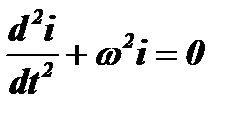Это классическое однородное (без правой части), линейное дифференциальное уравнение с постоянными коэффициентами. Его решение (полный интеграл) имеет вид:

,

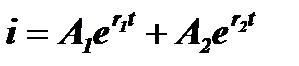где A₁ и A₂ – постоянные интегрирования, а r₁ и r₂ – решения алгебраического уравнения, которое называется характеристическим. У характеристического алгебраического уравнения каждый член имеет степень, равную порядку производной соответствующего члена дифференциального уравнения. Для решения дифференциального уравнения для тока i необходимо найти величины A₁, A₂, r₁ и r₂.

Характеристическое уравнение имеет вид: r²+w²=0. Решение этого уравнения: r²=–w². Получив корни уравнения: 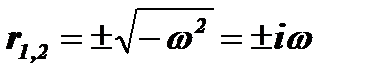, можно переписать решение дифференциального уравнения в виде:

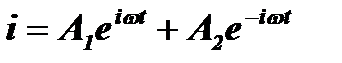.(2)

Постоянные интегрирования A₁ и A₂ находятся из начальных условий, которые имеются в контуре в начале процесса при t = 0, когда ток i=0. Тогда А₁+А₂=0, откуда А₁= –А₂.

С другой стороны при t=0 конденсатор заряжен полным напряжением источника U и поэтому 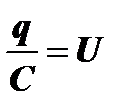. Поскольку 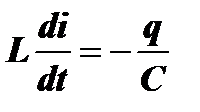, то при t=0 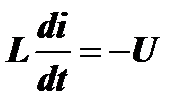, а .

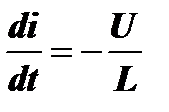Дифференцируя (2) получим 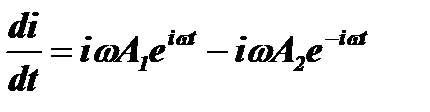. При t=0 это уравнение примет вид: 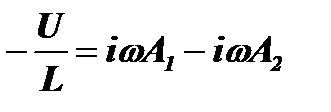. Учитывая, что А₁= –А₂, получим: 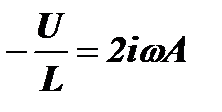. Отсюд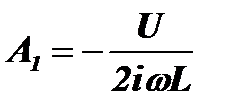а: , а .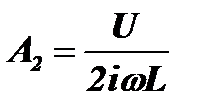

Тогда решение дифференциального уравнения для тока в контуре, выглядит следующим образом:

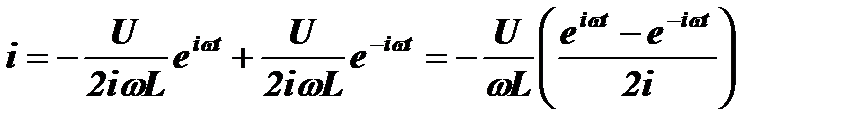
Знак минус получился потому, что за положительное направление принято направление тока при заряде конденсатора.

В свою очередь, заряд конденсатора, равный 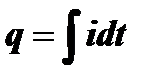, будет изменяться по закону: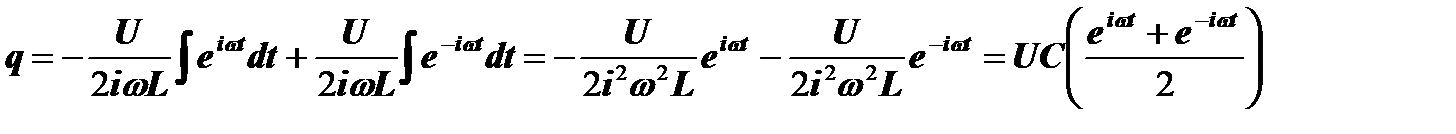

Выражения в скобках описывают периодические функции, главной особенностью которых является равенство самой функции и ее второй производной и подстановка решения в дифференциальное уравнение приводит его к нулю. Выражения, полученные в скобках, весьма громоздки и не удобны для записи и расчетов. Поэтому Эйлер ввел сокращенные обозначения этих функций, которые вошли в математику под его именем:

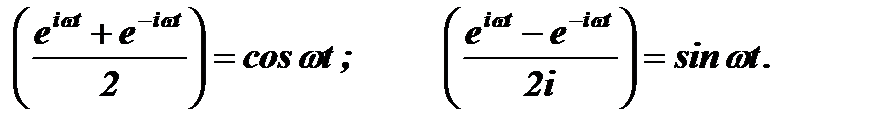
Графически эти функции описываются гармоническими колебаниями, которые являются основными функциями современной радиотехники – синусоида и косинусоида.

Теперь выражения для тока и заряда примут окончательный вид:

, .

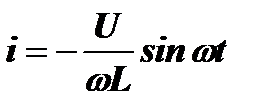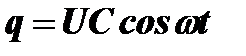Подставим для проверки выражение для тока в исходное дифференциальное уравнение:

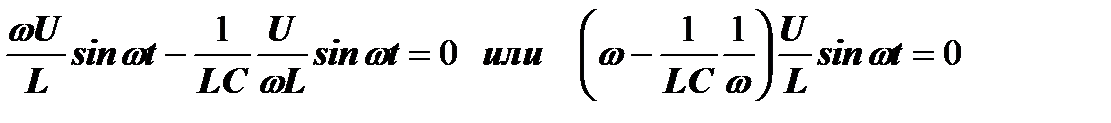
Равенство нулю будет получено при условии: .

Таким образом, мы видим, что введенное ранее обозначение w – это собственная частота колебаний контура, которая определяется значениями емкости и индуктивности контура и обычно обозначается w₀.

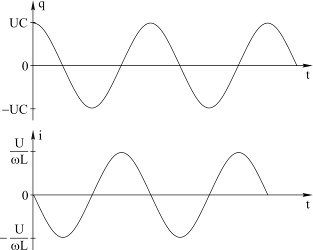
Рис. 4.10

На рисунке 4.10 приведены графики изменения заряда q и тока i в LC контуре. Они полностью соответствуют рассмотренной выше физической картине «перекачки» энергии из конденсатора в индуктивность и обратно.

О синусоиде. Следует отметить, что гармонические функции, полученные при решении уравнения для LC контура, используются также в тригонометрии для определения зависимости между катетами и гипотенузой в прямоугольном треугольнике от угла j между ними. При изменении этого угла проекция катета на одну ось ординат описывает синусоиду, а на другую ось – косинусоиду. Однако прямой связи между решениями дифференциального уравнения для LC контура и тригонометрическими функциями не видно.

Гармонические функции имеют уникальные свойства:

1. Все производные от нее являются также гармоническими функциями.

2. Все интегралы от нее также являются гармоническими функциями.

3. Сумма любого числа гармонических функций одной частоты с любыми амплитудами и фазами – всегда гармоническая функция той же частоты.

Эти свойства значительно облегчают проектирование радиотехнических систем и входящих в их состав устройств, в тех случаях, когда гармонические функции являются несущими колебаниями для сигналов, используемых в этих системах.

Процессы в контуре без потерь при включении внешней ЭДС.

Включим в контур без потерь источник внешней гармонической ЭДС. Этот источник можно включить последовательно или параллельно элементам контура (рис. 4.10,а). В первом случае в контуре будет общий ток и различные падения напряжения на каждом из элементов контура. Во втором случае на элементах контура будет общее падение напряжения и различные токи в каждом элементе. Поскольку для изучения резонанса расположение источника ЭДС и элементов контура не является принципиальным, в дальнейшем мы будем рассматривать только последовательный контур, обращаясь к параллельному контуру в тех случаях, когда это будет принципиально важно. Примем внешнюю гармоническую ЭДСравной u=Usinw_pt,где частота w_p отличается от собственной частоты контура w₀. В последовательном контуре u_L+u_C=u,что позволяет записать линейное неоднородное дифференциальное уравнение контура в виде:

.

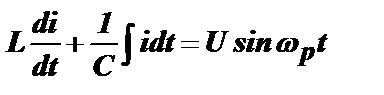Решение этого уравнения более громоздко, чем для однородного дифференциального уравнения. Поэтому сразу рассмотрим результат этого решения для напряжения на конденсаторе контура u(t)=q(t)/C:

.

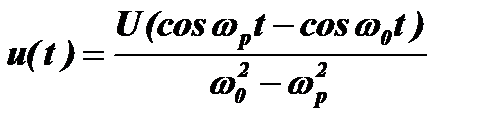Из решения видно, что при подаче внешнего гармонического сигнала на контур в нем возникают два одинаковых по амплитуде U колебания, начинающихся в противофазе (знак минус между ними). Одно колебание (называемое вынужденным) имеет частоту внешнего сигнала w_p, а другое (называемое свободным) – частоту собственных колебаний контура w₀. Пользуясь тригонометрическими преобразованиями, раскроем это выражение:

.

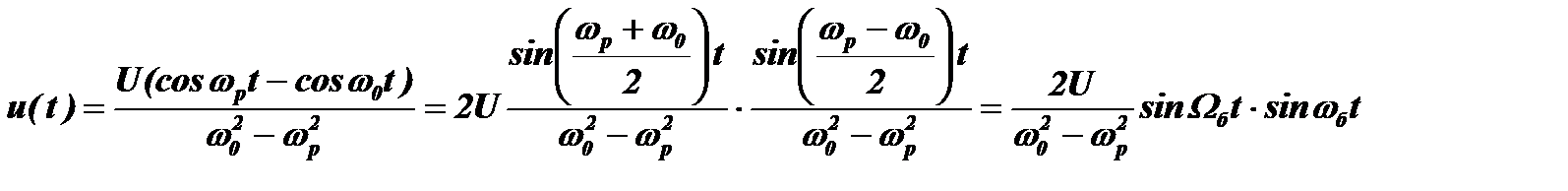Биения. Если w_p и w₀ достаточно близки между собой, то u(t) представляет собой периодическую функцию (рис. 4.11), которая называется «биения». Частота заполнения биений равна w_б=(w_р + w₀)/2, а частота огибающей W_б= │(w_р - w₀)/ 2 │.

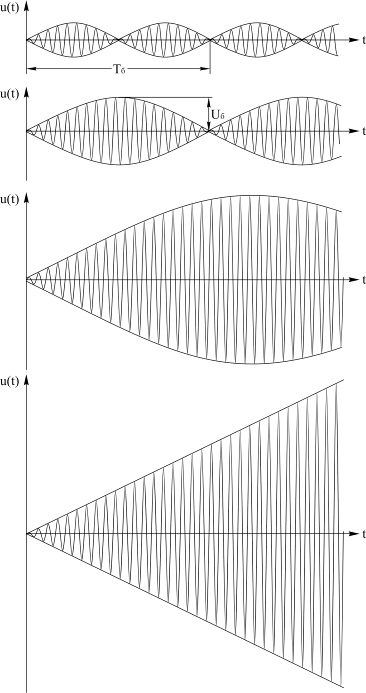
Рис. 4.11

Чем ближе друг к другу частоты w_p и w₀, тем больше амплитуда 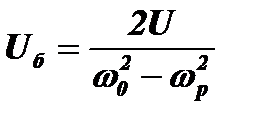и тем больше период T_б=2p¤W_б, (три верхние диаграммы на рис. 4.11, где разность между частотами w_p и w₀ последовательно уменьшается в два раза). Если потерь в контуре нет, то биения будут продолжаться, пока будет действовать источник внешней ЭДС.

Важным для нас является случай, когда w_p=w₀. Выражение для напряжения на конденсаторе контура в этом случае приводит к неопределенности вида 0/0, которую можно раскрыть по правилу Лопиталя:

.

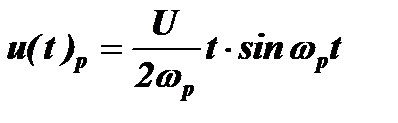В этом случае с ростом t колебания нарастают неограниченно (нижняя диаграмма на рис. 4.11). Это и есть резонанс в контуре без потерь, представленный в области времени.

Контур с потерями. В реальном контуре всегда есть потери и свободные колебания будут затухать, если потери не компенсируются притоком энергии извне.

Процессы в контуре с потерями во временной области. Параметры контура.

Рассмотрим колебание, возникающее в контуре с потерями при разряде конденсатора, имеющего начальный заряд q. Уравнение Кирхгофа в этом случае имеет вид: u_L+u_C+u_R=0, где: 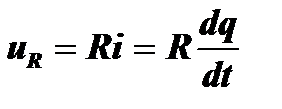. Тогда дифференциальное уравнение контура для заряда q(t) примет вид:

.

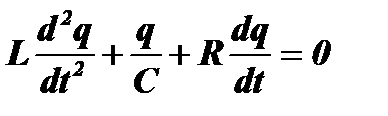Обозначим 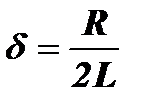и перепишем это уравнение в виде:

.

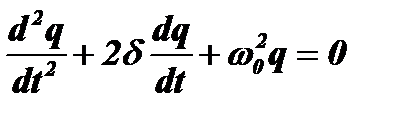Строгое решение этого однородного, линейного дифференциального уравнения позволяет получить выражение для изменения заряда и, соответственно, напряжения на конденсаторе:

,

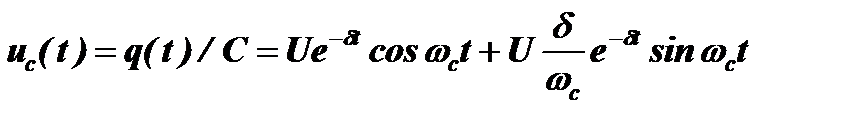где: U= q/C, а 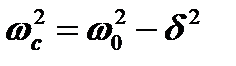− собственная частота контура. Поэтому в контуре с потерями собственная частота колебаний отличается от резонансной. Однако для добротного контура обычно δ<<ω₀ и поэтому принято полагать ω_с≈ ω₀. В этом случае (рис. 4.12):

u_с(t)=q(t)/C ≈Ue^-δtcosω₀t.

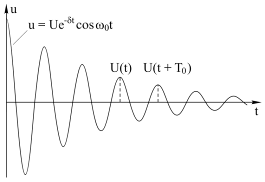
Рис. 4.12

Отношение: 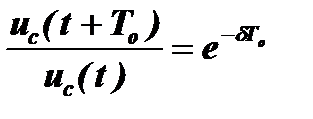показывает скорость затухания амплитуды колебаний за один период T_o. Величина δT_o=d называется логарифмическим коэффициентом затухания контура, поскольку 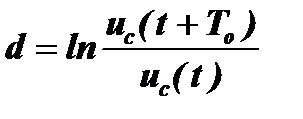. Величина, обратная этому коэффициенту, 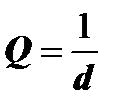называется добротностью контура.

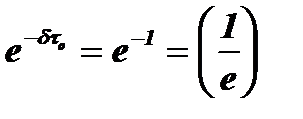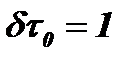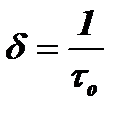Промежуток времени, за который амплитуда колебаний в контуре уменьшится в e раз (2,7 раза), называется постоянной времени контура t_o. Тогда , откуда и . Величина 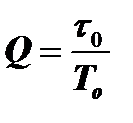показывает насколько постоянная времени контура превосходит период его колебаний.

Процессы в контуре с потерями при включении внешней ЭДС. При включении в контур с потерямивнешней гармонической ЭДС u=Usinw_pt (рис. 4.13), уравнение Кирхгофа имеет вид u_L+u_R+u_C=u(t) или в дифференциальной форме:

.

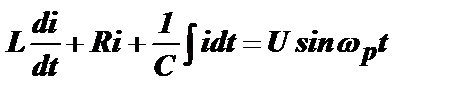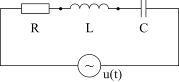
Рис. 4.13

Как и в контуре без потерь в момент включения внешней ЭДС здесь возникают два колебания - вынужденное с частотой внешнего сигнала w_p, и свободное с частотой собственных колебаний контура w₀, которые имеют одинаковую амплитуду и начинаются в противофазе. Это значит, что при включении внешней ЭДС с w_p¹w₀ в контуре также возникнут биения. Однако в этом случае свободное колебание с частотой w₀ будет затухать и через время, равное постоянной времени t₀, в контуре останутся только вынужденные колебания с частотой w_p (рис. 4.14).

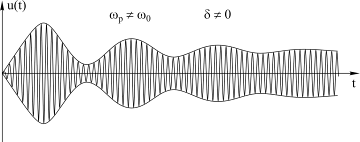
Рис. 4.14

При w_p=w₀ напряжение на конденсаторе контура описывается приближенной формулой:

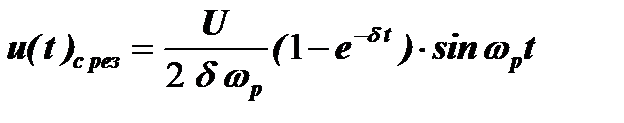
Это и есть резонанс в контуре с потерями, представленный в области времени. Изменение этого напряжения при различных значениях величины d=R/2L показано на рисунке 4.15.

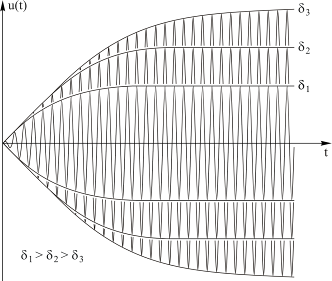
Рис. 4.15

При t®¥ амплитуда напряжения на конденсаторе контура стремится к постоянному значению:

.

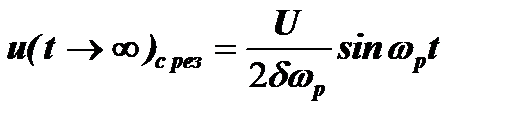Влияние потерь на процессы в контуре. Потери приводят к разделению колебательного процесса в контуре на две части: нестационарный или переходной режим, который возникает после включения внешней ЭДС и характеризуется изменением амплитуды колебаний; стационарный или установившийся режим, в который переходит контур, когда в нем остаются колебания с постоянной амплитудой. Переход в стационарный режим при резонансе определяется потерями в контуре, которые растут с ростом амплитуды колебаний. При некотором значении этой амплитуды энергия, поступающая в контур от источника внешней ЭДС в каждом периоде колебаний, становится равной потерям энергии в активном сопротивлении контура. В результате рост амплитуды колебаний в контуре прекращается. Чем меньше потери в контуре и чем больше постоянная времени контура t₀, тем дольше существует нестационарный режим. В пределе, при R®0, нестационарный режим будет продолжаться бесконечно долго (нижняя диаграмма на рис. 4.11) и в стационарный режим контур не перейдет вообще. Ограничением роста амплитуды колебаний в контуре в этом случае является переход элементов контура в нелинейный режим, сопровождающийся эффектами типа пробоя или перегрева (сгорания).

Механизм возникновения резонанса.

Нас, как и раньше, интересует ответ на два вопроса:

1. От чего зависит сопротивление контура переменному току?

2. Чем определяется сдвиг по фазе между ЭДС источника и протекающим по контуру током?

Рассмотрим физическую картину процессов, происходящих в контуре. В стационарном режиме между мгновенным значением тока, протекающего в цепи, и мгновенными значениями падений напряжения на элементах контура, сохранятся такие же фазовые соотношения: u_R - совпадает по фазе с током, u_L – опережает ток по фазе на p¤2, u_C – отстает от тока по фазе на p¤2. Сдвиг между u_L и u_C по фазе на p¤2 в разные стороны относительно тока i означает, что между собой эти два напряжения сдвинуты по фазе на p, то есть находятся в противофазе. Суммарная амплитуда напряжения U_L+U_C будет зависеть от того, какая из двух амплитуд будет больше: U_L=IX_L или U_C=IX_C. Учитывая, что ток I в цепи общий, суммарная амплитуда напряжения будет определяться амплитудными значениями реактивных сопротивлений X_L и X_C. Их алгебраическая сумма равна w_рL–1¤w_рC. Если w_рL>1¤w_рC, то преобладает амплитуда напряжения на индуктивности U_L, а контур имеет реактивное индуктивное сопротивление w_рL'=w_рL–1¤w_рC. Очевидно, что при этом контур может быть представлен в виде эквивалентной индуктивности L'. Если w_рL<1¤w_рC, то преобладает амплитуда напряжения на емкости U_C, общее реактивное сопротивление контура будет емкостным: –1¤w_рC'=w_рL–1¤w_рC, а контур может быть представлен в виде эквивалентной емкости С'.

Наиболее важным для нас является случай, когда мгновенные значения реактивных сопротивлений становятся равны x_L=x_C. Тогда 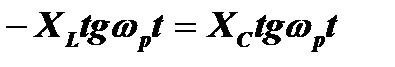, а амплитудные значения реактивных сопротивлений будут равны и противоположны по знаку X_L=–X_C. В этом случае и амплитуды напряжений на емкости и индуктивности: U_L= –U_C будут равны и противоположны по знаку. В результате они скомпенсируют друг друга, что эквивалентно взаимной компенсации реактивных сопротивлений X_L и X_C. Тогда нагрузкой источника ЭДС будет только активное сопротивление контура R. А поскольку величина R в колебательном контуре мала по сравнению с величинами реактивных сопротивлений емкости и индуктивности, это приведет к значительному росту амплитуды тока в контуре. Это и есть резонанс в линейном последовательном колебательном контуре с постоянными параметрами. Поскольку этот вид резонанса связан с взаимной компенсацией реактивных сопротивлений емкости и индуктивности, мы назовем его компенсационным резонансом.

Поскольку абсолютные значения амплитуд реактивных сопротивлений при резонансе равны X_L=X_C то:

,

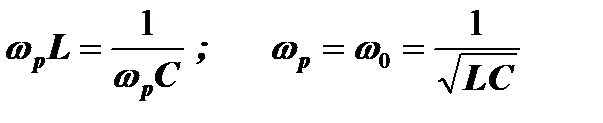что подтверждает равенство частот внешних колебаний w_р собственной частоте колебаний контура w₀ при этом виде резонанса.

Частотная характеристика контура. Рассмотрим как проявляется резонанс в частотной области. Для этого определим зависимость амплитуды и фазы колебаний в контуре от частоты.

Из векторной диаграммы напряжений и токов в контуре, изображенной на рисунке 4.16., видно, что напряжение внешней ЭДС U и падения напряжения на элементах контура U_R и U_L–U_C связаны между собой соотношением: U²=I²R²+I²(ωL-1/ωC)².

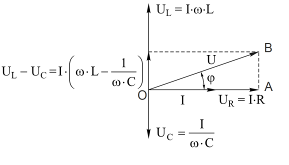
Рис. 4.16

Тогда зависимости амплитуды тока в контуре I и фазового сдвига j между этим током и внешней ЭДС от частоты будут равны:

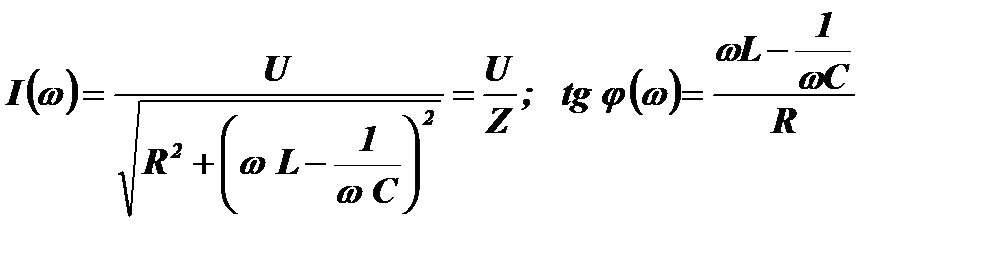
Величина Z называется полным сопротивлением цепи или импедансом.

При резонансе U_L=U_С, ωL=1/ωC, а 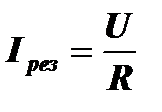и j_рез=nπ, где n=0,±1,±2±3.... Нормированная к резонансному значению величина тока в контуре будет равна:

.

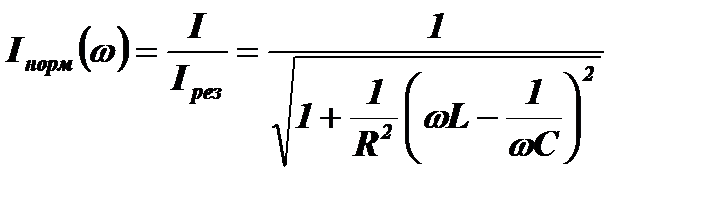Представляет интерес зависимость I_норм от добротности контура Q и ширины его полосы частот ∆ω. Эту зависимость определим, преобразуя выражение, стоящее под корнем:

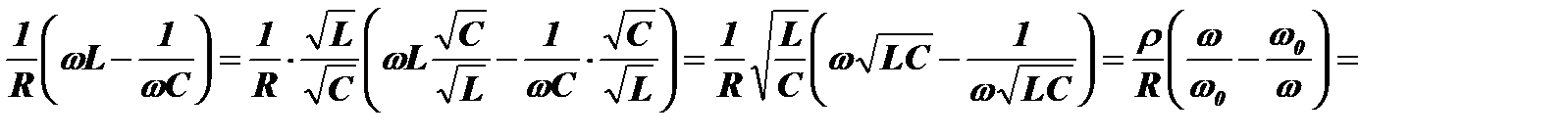
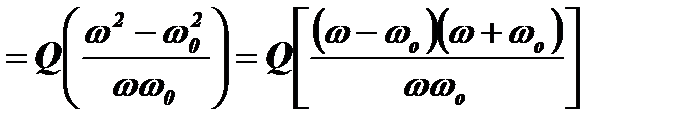. Упростим полученное выражение, пользуясь узкой полосой контура, которая позволяет полагать ω≈ω₀. Тогда 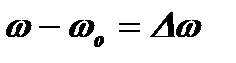, , 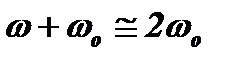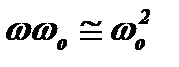. Тогда 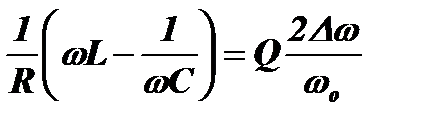. Подставляя это выражение в формулу для I_норм, получим: .

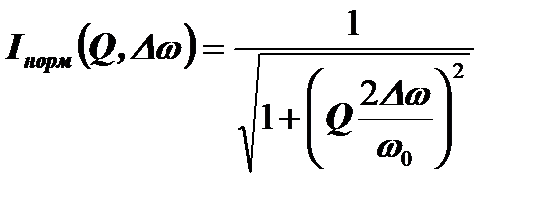На рисунке 4.17 приведены амплитудная и фазовая характеристики контура, показывающие зависимости I(w) и j(w) от частоты w.

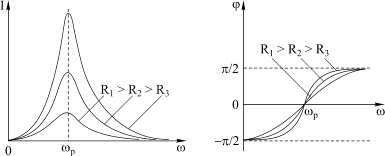
Рис. 4.17

Из графиков видно, что с уменьшением потерь в контуре растет амплитуда колебаний при резонансе. На частотах ниже резонансной емкостное сопротивление контура объясняется тем, что напряжение меняется медленно и в результате на обкладках конденсатора накапливается больше зарядов и их отталкивающее действие по отношению к новым зарядам, поступающим от источника ЭДС, растет, что эквивалентно росту сопротивления. В результате ток отстает от внешнего напряжения, угол φ – отрицательный. На частотах выше резонансной индуктивное сопротивление контура объясняется тем, что с увеличением скорости изменения тока возрастает величина ЭДС индукции, препятствующей росту тока в контуре. В результате ток опережает внешнее напряжение, угол φ – положительный. И только на резонансной частоте контур имеет очень небольшое активное сопротивление, а φ угол равен нулю.

Вид амплитудных характеристик для нормированного тока 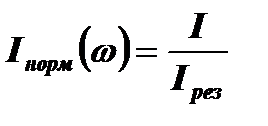показан на рисунке 4.18.

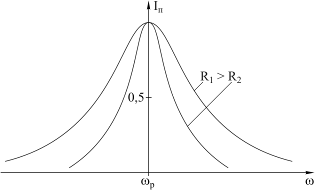
Рис. 4.18

Возвращаясь к вопросу разделения колебательного процесса в контуре на две части: нестационарный или переходной режим и стационарный или установившийся режим, и к определению момента перехода от одного режима к другому, следует указать, что резонансная характеристика, резонансная кривая контура, которую мы рассмотрели, формируется только в стационарном режиме и пользоваться ею можно только после установления колебаний, а не в переходном режиме сразу после подачи в контур внешней ЭДС.