Го порядка с постоянными коэффициентами
Дифференциальное уравнение вида
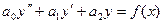 ,
,
где 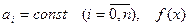 - известная функция, называющаяся линейными дифференциальным уравнением n-2-го порядка с постоянными коэффициентами.
- известная функция, называющаяся линейными дифференциальным уравнением n-2-го порядка с постоянными коэффициентами.
Если 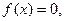 то уравнение называется однородным, в противном случае – неоднородным.
то уравнение называется однородным, в противном случае – неоднородным.
Если f(x) – непрерывная функция, то общее решение уравнения состоит из суммы общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения.
Решение однородного уравнения
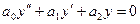
можно найти, используя алгебраические методы. Для этого заменяем производные на степенные функции, показатель степени которых соответствует порядку производной. Получаем характеристическое уравнение вида
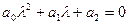 .
.
Общее решение однородного уравнения определяется в зависимости от вида корней характеристического уравнения.
Правило 1. (корни характеристического уравнения простые и действительные).Если корни характеристического уравнения различные действительные числа  , то общее решение уравнения имеет вид:
, то общее решение уравнения имеет вид: 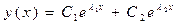 , где
, где 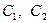 - произвольные постоянные.
- произвольные постоянные.
Правило 2. (корни характеристического уравнения комплексно-сопряженные).Если корни характеристического уравнения комплексно-сопряженные числа 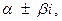 то общее решение уравнения имеет вид:
то общее решение уравнения имеет вид: 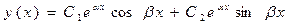 , где
, где 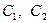 - произвольные постоянные.
- произвольные постоянные.
Правило 3. (корни характеристического уравнения действительные, кратные).Если корни характеристического уравнения равные действительные числа 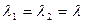 , то общее решение уравнения имеет вид:
, то общее решение уравнения имеет вид:  ,где
,где 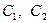 - произвольные постоянные.
- произвольные постоянные.
Частное решение неоднородного уравнения может быть подобрано по виду правой части. Если правая часть – постоянная величина, то частное решение дифференциального уравнения имеет вид:
- 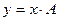 , если нуль является корнем характеристического уравнения;
, если нуль является корнем характеристического уравнения;
-  , если нуль не является корнем характеристического уравнения.
, если нуль не является корнем характеристического уравнения.
Здесь А произвольная постоянная, для определения значения которой частное решение подставляется в исходное дифференциальное уравнение.
ЧИСЛОВЫЕ РЯДЫ
Дата добавления: 2016-03-22; просмотров: 702;
