Апериодическое звено первого порядка
Апериодическим звеном первого порядка называется такое звено, выходная величина которого в функции времени изменяется по экспоненциальному закону. Апериодические звенья называют также инерционным, статическим, релаксационным, одноёмкостным и др.
Инерционное звено описывается дифференциальным уравнением первого порядка
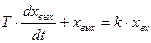 ,
,
где T – постоянная времени звена (T>0);
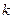 – коэффициент передачи (усиления) звена.
– коэффициент передачи (усиления) звена.
|
|
|
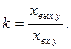
К апериодическим звеньям можно отнести: R-L и R-C цепи, генераторы постоянного тока, фильтры, термисторы, механические устройства, имеющие массу и силу трения (без пружин) и другие подобные устройства, в которых возможно накопление какого-либо вида энергии и её рассеивания.
Операторное уравнение апериодического звена
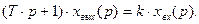
Передаточная функция звена
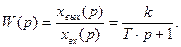
На структурных схемах графически инерционное звено изображается следующим образом:

Временная характеристика, представляющая реакцию звена на ступенчатое воздействие xвх(t)=1(t), определяется зависимостью 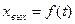 .
.
Выходная величина в переходном режиме определяется
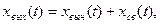
где вынужденная составляющая выходной величины
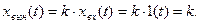
Cвободная составляющая выходной величины xвых(t) определяется из следующего выражения
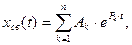
где Pk – корни характеристического уравнения звена
Tp+1=0,
т.е. 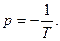
Отсюда 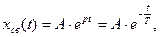
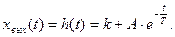
Начальное значение для переходной функции найдется
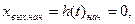 при t=0,
при t=0,
т.е. 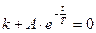
или 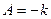
Окончательно получаем следующее выражение для переходной функции:
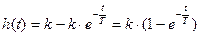 (3.11)
(3.11)
или 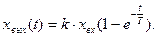 (3.12)
(3.12)
На рис.3.5,а приведена временная характеристика, представляющая собой экспоненту. Время достижения установившегося значения
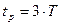 при
при 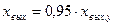 ,
, 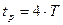 при
при 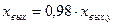 .
.
|

Весовая функция
|
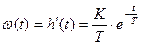
представлена на рис.3.5,б.
На структурных и функциональных схемах апериодические звенья условно изображаются следующим образом

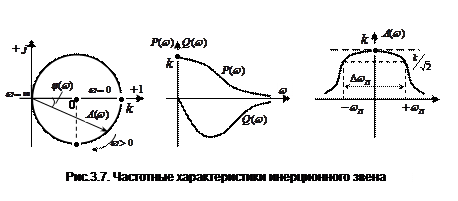
Амплитудно-фазовая характеристика апериодического звена
|
|
|
|
|
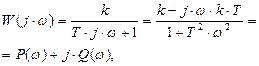
или
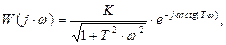
где 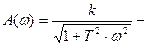 модуль вектора W (jω);
модуль вектора W (jω);
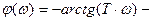 аргумент вектора W (jω).
аргумент вектора W (jω).
АФХ представляет собой окружность радиусом 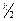 с центром в точке 0, лежащей на оси абсцисс на расстоянии
с центром в точке 0, лежащей на оси абсцисс на расстоянии 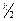 от начала координат.
от начала координат.
Уравнения вещественной и мнимой характеристик
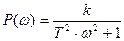
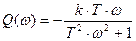
Логарифмическая амплитудная частотная характеристика (ЛАЧХ) может быть получена путём логарифмирования выражения для A(ω).
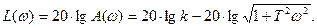
В этом выражении слагаемое 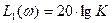 представляет постоянную величину, не зависящую от частоты. Рассмотрим вторую составляющую ЛАЧХ
представляет постоянную величину, не зависящую от частоты. Рассмотрим вторую составляющую ЛАЧХ
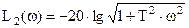 .
.
Полагая, что 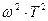 <<1
<<1 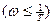 , получим
, получим 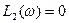 .
.
Если 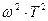 »1
»1 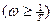 , пренебрегаем единицей и получаем
, пренебрегаем единицей и получаем 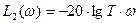 , что соответствует наклону характеристики, равному
, что соответствует наклону характеристики, равному 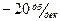 .
.

ЛАЧХ апериодического звена может быть получен как сумма 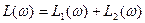 , т.е. суммированием ординат этих двух кривых (рис.3.8). Следовательно, приближённая ЛАЧХ состоит из двух асимптот. Первая представляет прямую, параллельную оси абсцисс и отстоит от неё на расстоянии
, т.е. суммированием ординат этих двух кривых (рис.3.8). Следовательно, приближённая ЛАЧХ состоит из двух асимптот. Первая представляет прямую, параллельную оси абсцисс и отстоит от неё на расстоянии 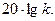 Вторая наклонена к оси абсцисс с наклоном
Вторая наклонена к оси абсцисс с наклоном 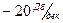 . Сопряжение горизонтальной и наклонной прямой производится в точке, соответствующей частоте сопряжения
. Сопряжение горизонтальной и наклонной прямой производится в точке, соответствующей частоте сопряжения 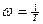 . Частота, при которой L(ω) пересекает ось абсцисс, называется частотой среза.
. Частота, при которой L(ω) пересекает ось абсцисс, называется частотой среза.
Приближённая ЛАЧХ называется асимптотической. Такое название связано с тем, что эта характеристика составлена из двух асимптот, к которым стремится ЛАЧХ при ω→ 0 и ω→ ∞.
При 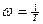
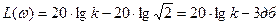
Т.о., максимальное расхождение между истинной и асимптотической ЛАЧХ равно всего 3дб. Поэтому при практических построениях ЛАЧХ статических звеньев первого порядка используют обычно асимптотические ЛАЧХ.
Если частотные характеристики получены экспериментально, по ним нетрудно определить параметры звена T и k, пользуясь описанной выше зависимостью между этими характеристиками и передаточной функцией.
На примере этого звена явно видно, что величина полосы пропускания звеном частот, т.е. ширина частотной характеристики, является мерой быстродействия звена. Полоса пропускания частот обычно определяется диапазоном частот от 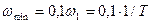 , на декаду меньшей минимальной частоты сопряжения, до
, на декаду меньшей минимальной частоты сопряжения, до 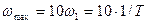 , на декаду большей максимальной частоты сопряжения. Чем больше этот диапазон частот, тем короче его переходная характеристика, т.е. меньше инерционность звена.
, на декаду большей максимальной частоты сопряжения. Чем больше этот диапазон частот, тем короче его переходная характеристика, т.е. меньше инерционность звена.
Дата добавления: 2016-03-20; просмотров: 12923;