Временные характеристики звена
Если характеристическое уравнение не имеет кратных и нулевых корней, переходная функция h(t) определяется с помощью обратного преобразования Лапласа. Если передаточную функцию представить в виде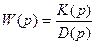 
, то в соответствии с обратным преобразованием Лапласа
|
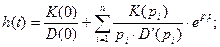
Для рассматриваемого звена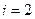 
Корни характеристического уравнения
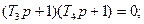
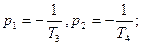
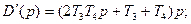
Следовательно
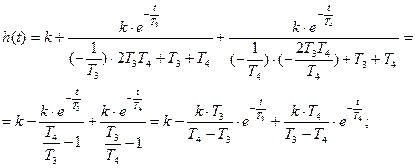
или
|
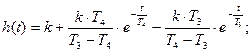
при T3>T4..
На рисунке 3.15 представлены кривые переходного процесса инерционного звена 2-го порядка (его составляющие). Из графиков видно, что меньшие (малые) постоянные времени влияют на начало переходного процесса, а большие постоянные времени определяют среднюю часть и окончание процесса.
|
Время переходного процесса (регулирования) может быть определена
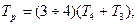
Импульсная (весовая) переходная функция
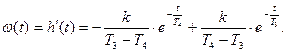
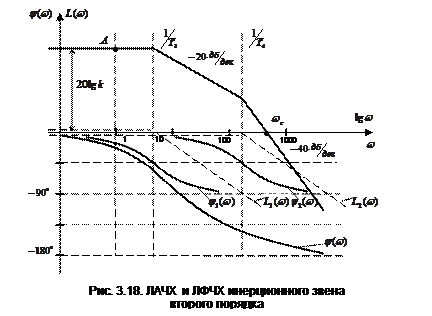
Частотные характеристики звена
АФЧХ инерционного звена 2-го порядка имеет вид (рис.3.16)
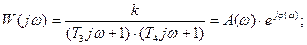
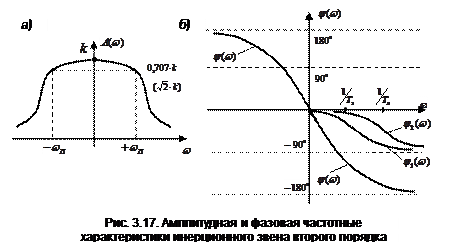
Амплитудно-частотная характеристика A(ω) (рис. 3.17,а)
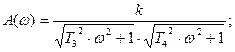
Фазо-частотная характеристика φ(ω) (рис.3.17,б)
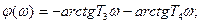
Дата добавления: 2016-03-20; просмотров: 1016;