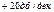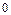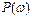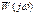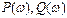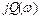Временные характеристики
Порядок числителя передаточной функции W(p) больше порядка знаменателя. В этом случае переходную функцию целесообразно искать в виде суммы переходных функций h(t) составляющих звеньев (рис. 3.42.).
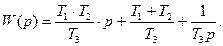
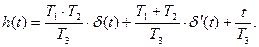

Частотные характеристики
АФХ: 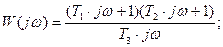
АЧХ: 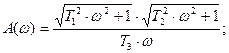
ФЧХ: 
ЛАХ:
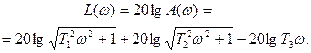
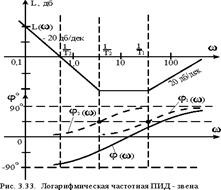
Логарифмические частотные характеристики представлены на рис. 3.43.



| Рис. 3.43. Логарифмические частотные характеристики ПИД - звена
| |
Запаздывающее звено
Запаздывающее звено – это звено, которое на выходе воспроизводит входной сигнал без искажений, однако с некоторым постоянным запаздыванием  .
.
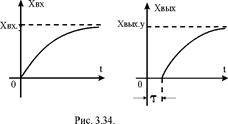 Уравнение запаздывающего звена
Уравнение запаздывающего звена
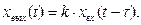
Уравнение в операторном виде
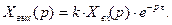
Передаточная функция

Амплитудно-фазовая характеристика
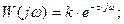












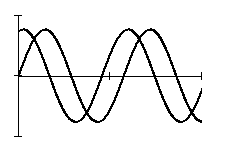
Графически АФХ может быть представлена окружностью с центром в начале координат с радиусом, равным k.
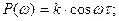
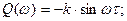
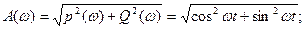
Логарифмическая амплитудная частотная характеристика
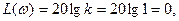 т.е. совпадает с осью абсцисс.
т.е. совпадает с осью абсцисс.
ГЛАВА 4. СТРУКТУРНЫЕ СХЕМЫ САР И ИХ ПРЕОБРАЗОВАНИЯ
Дата добавления: 2016-03-20; просмотров: 759;
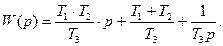
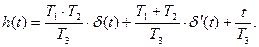

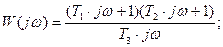
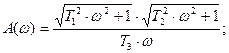

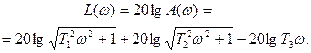




 .
.
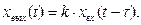
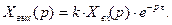

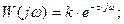













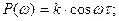
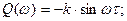
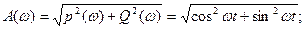
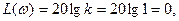 т.е. совпадает с осью абсцисс.
т.е. совпадает с осью абсцисс.