Построение частотных характеристик разомкнутой системы по частотным характеристикам звеньев

По передаточной функции системы можно вычислить ее частотные

характеристики. Это же можно выполнить и графически. Например, если задана передаточная функция системы

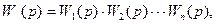(4.21)

то можно записать

(4.22)

При перемножении комплексных чисел их модули перемножаются, а аргументы (фазы) складываются. Поэтому модуль суммарного вектора

будет , а фаза .

Выражение (4.22) позволяет находить суммарную АФХ по характеристикам отдельных звеньев.

где - амплитудно-фазовая частотная характеристика I-го звена.

Отсюда амплитудно-фазовая частотная характеристика разомкнутой системы определится

(4.22)

и фазовая частотная характеристика

(4.23)

На рис.4.18 приводится по­строение АФХ разомкнутой системы по АФХ отдельных звеньев. Построение АФХ разомкнутой системы при последовательном соединении звеньев производится по амплитудно-фазовым характеристикам отдельных звеньев в соответствии с выражениями (4.20) и (4.21).

Построение представлено на рис.4.18. Здесь A₁(ω) и A₂(ω) – модули АФХ при определенной частоте, а 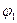и 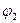- аргументы (фазы) при той же частоте. Суммарный модуль разомкнутой системы определяется и фаза

Проделав аналогичное построение для других частот при изменении их от до , можно получить АФЧХ всей системы в целом.

Можно показать, что, если для одного инерционного звена АФХ имеет вид, приведенный на рис.4.19,а, то при последователь­ном соединении двух звеньев на рис.4.19,б и для трех звеньев - на рис.4.19,в.

Добавление инерционного звена с передаточной функцией означает поворот вектора по фазе на угол, равный Следовательно, максимальный фазовый угол час­тотной характеристики растет по мере увеличения в системе числа инер­ционных звеньев. Очевидно, что эта тенденция роста фазового угла должна наблюдаться также и при увеличении числа колебательных звеньев в системе.

Включение одного интегрирующего звена, имеющего АФХ, совпа­дающую с мнимой осью в ее отрицательной части, приводит к повороту всех векторов характеристики на угол, равный -90°, по часовой стрелке при одновременной умножении их модулей на модуль интегрирующего звена, т е. на , где k и Т - параметры звена. Например, если система имеет АФХ 1, представленную на рис.4.20, то при последова­тельном включении одного интегрирующего звена с характеристикой 2, получим суммарную характеристику 3.

Последовательное включение двух интегрирующих звеньев в од­ноконтурную систему, составленную из инерционных и колебательных звеньев, приводит к повороту всех векторов АФХ на угол, равный , т е. создаёт большое фа­зовое отставание выходного сигна­ла от входного.