Построение логарифмических частотных характеристик
Зная логарифмические частотные характеристики отдельных динамических звеньев и пользуясь методикой их построения, сравнительно просто можно построить логарифмические частотные характеристики для разомкнутых CAP.
Рассмотрим правила построения логарифмических частотных характеристик группы последовательно соединённых элементов. Так как при последовательном соединении звеньев
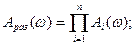
то, логарифмируя это равенство, можно записать
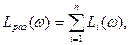
где 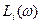 - ЛАЧХ отдельного звена.
- ЛАЧХ отдельного звена.
Точно также логарифмическая фазовая частотная характеристика (ЛФЧХ) разомкнутой системы определяется
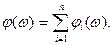
Как следует из последних выражений, ЛАЧХ и ЛФЧХ разомкнутой системы при последовательном соединении звеньев могут быть получены путем суммирования ординат и характеристик отдельных звеньев. В качестве примера рассмотрим построение характеристик CAP при последовательном соединении одного интегрирующего и двух инерционных звеньев (рис.4.21).
Логарифмические частотные характеристики данной системы могут быть построены более упрощенно без построения характеристик отдельных звеньев. Для этого воспользуемся следующей методикой.
1. Определяются и наносятся на ось частот полулогарифмической сетки сопряжённые частоты звеньев. Для рассматриваемого примера сопряжённые частоты звеньев находятся
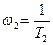 и
и 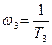 при
при 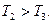
При 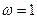 откладывается ордината ЛАЧХ, равная 20lgk , где k-суммарный передаточный коэффициент последовательно соединенных звеньев, т.е.
откладывается ордината ЛАЧХ, равная 20lgk , где k-суммарный передаточный коэффициент последовательно соединенных звеньев, т.е.
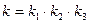 .
.
На оси абсцисс удобно указывать наряду с 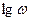 непосредственно и значение ω.
непосредственно и значение ω.
2. Через полученную точку А проводится низкочастотная часть ЛАЧХ т е участок ЛАЧХ, расположенный левее наименьшей сопряжённой частоты Эта часть характеристики имеет наклон, равный 20(m-r) дб/дек, где m - число дифференцирующих, а r - число интегрирующих звеньев. Указанный участок характеристики проводится слева направо до пересечения с вертикальной прямой, проходящей через наименьшую сопряжённую частоту (в нашем случае ω2). Если в схеме отсутствует интегрирующие и дифференцирующие звенья (множители p в знаменателе и числителе), то проводится прямая, параллельная оси абсцисс. В рассматриваемом примере наклон этого участка ЛАЧХ равен 20·(0 - 1) = -20 дб/дек.
3. При частоте сопряжения ω2 производится излом асимптоты ЛАЧХ в соответствии с типом звена, которому принадлежит данная сопрягающая частота. Частота ω2 соответствует инерционному звену, поэтому наклон характеристики изменяется на -20 дб/дек, т.е. становится равным -40 дб/дек. Участок ЛАЧХ с этим наклоном проводится до следующей сопрягающей частоты ω3. Следует заметить, что при дифференцирующем звене наклон изменяется на +20 дб/дек, а при колебательном звене – на -40 дб/дек. Для колебательного звена при необходимости производится поправка, т.е. строится реальная ЛАЧХ в области частоты сопряжения.
При частоте 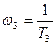 наклон характеристики опять изменится на -20 дб/дек и становится равным -60 дб/дек.
наклон характеристики опять изменится на -20 дб/дек и становится равным -60 дб/дек.

Таким же образом характеристика L(ω) продолжается в сторону увеличения частоты, претерпевая последовательно изломы на каждой сопрягающей частоте.
Построение логарифмических фазовых частотных характеристик ЛФЧХ последовательно соединённых звеньев выполняется либо при помощи специальных лекал, либо табличным способом, который во многих случаях оказывается и более простым и более точным.
Для рассматриваемой системы суммарная фаза разомкнутой системы определится по выражению
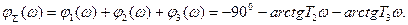
Расчет фазовой частотной характеристики производится в виде следующей таблицы:
Таблица 4.1
Частота
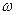 , 1/с , 1/с
| 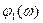
| 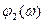
| 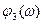
| 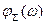
|
Расчет производится в диапазоне от 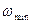 до
до 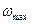 , где
, где 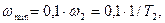
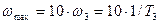 . Этим диапазоном будет определяться полоса пропускания частот системы.
. Этим диапазоном будет определяться полоса пропускания частот системы.
Дата добавления: 2016-03-20; просмотров: 1513;
