Передаточные функции замкнутой системы по отношению к задающему и возмущающему воздействиям

В замкнутой системе регулируемая величина 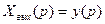через

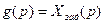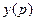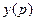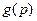обратную связь подается на её вход (на элемент сравнения). В общем случае к системе приложены задающее и возмущающее воздействие F(p). Оба эти воздействия оказывают влияние на регули­руемую величину . Поэтому при анализе замкнутой системы необхо­димо рассматривать передаточные функции, связывающие с и 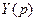с F(p) .

В качестве примера рассмотрим одноконтурную CAP, схема которой представлена на рис.4.23.

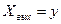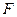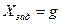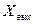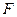К этой схеме можно свести все одноконтурные CAP, струк­турные схемы которых могут со­держать вместо указанных звеньев любое число последова­тельно или параллельно соединённых звеньев, а также звеньев, охваченных местными обратны­ми связями. Здесь - выходная регулируемая величина, - воз­мущение, а - задающее воздействие. Выведем выражения для передаточных функций, связывающих с и .

Рассмотрим вначале передаточную функцию CAP по задающему воздействию.В этом случае 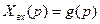и 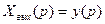.Следует отметить, что в одноконтурных CAP в качестве главной обратной связи применяется отрицательная обратная вязь. Это объясняется тем, что в замкнутых CAP используется принцип регулирова­ния «по отклонению» выходной величины от заданного значения. В этом случае все изменения выходной регулируемой величины, вызванные воз­мущениями, будут ликвидироваться в результате противоположного дей­ствия управляющего устройства CAP.

С учетом сказанного передаточная функция CAP по задающему воз­действию определится

(4.24)

где 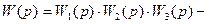передаточная функция разомкнутой САР в случае одиночной обратной связи;

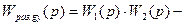передаточная функция разомкнутой системы при задающем воздействии .

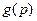Передаточная функция САР по возмущающему воздействию, связывающая выходную регулируемую величину 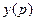с возмущающим воздействием , приложенным в произвольной точке системы, будет иметь вид

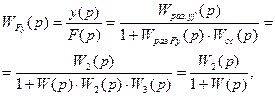(4.25)

где 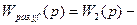передаточная функция разомкнутой системы при возмущающем воздействии .

Следовательно,

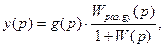(4.26)

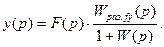(4.27)