Колебательного звена

Уравнение АФХ колебательного звена может быть получено непосредственно из его передаточной функции подстановкой j·ω вместо p.

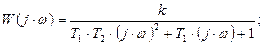
или

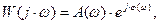
где A ( 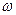) - модуль АФХ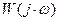

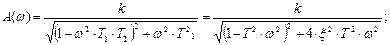
φ(ω) – аргумент амплитудно-фазовой характеристики звена.

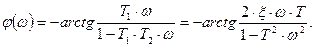
Частотные характеристики колебательного звена представлены на (рис.3.11).

АФЧХ W(j ) колебательного звена может быть получена экспериментально. В этом случае с её помощью можно определить параметры звена: k, ξ и T. Величина коэффициента k равна длине отрезка на вещественной оси от начала координат до точки АФЧХ при ω = 0.

Коэффициент ξ находится из выражения для отрезка

(рис 3.11, б), т.е.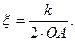

Величина постоянной времени .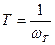

Логарифмические частотные характеристики колебательного звена

Логарифмическая амплитудная частотная характеристика (ЛАЧХ) звена может быть получена следующим образом:

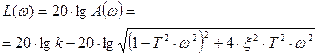(3.32)

Первое слагаемое представляет собой постоянную величину 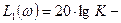прямую, параллельную оси абсцисс. Второе слагаемое зависит от частоты ω.

Если 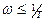, составляющим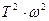и и 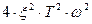можно пренебречь по сравнению с 1, поэтому .

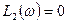Если , то выполняется условие 1<< .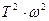

В этом случае

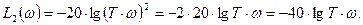
Очевидно, что при изменении частоты ω на декаду, значение изменится на –40дб. Следовательно, наклон при этом будет равен .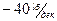

Таким образом, приближённая асимптотическая ЛАЧХ колебательного звена изображается двумя отрезками прямых: горизонтальным отрезком, при 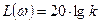и отрезком с наклоном 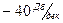. Низкочастотные и высокочастотные асимптоты ЛАЧХ сопрягаются при частоте сопряжения ω, определяемой из следующего уравнения 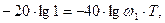т.е. при частоте .

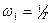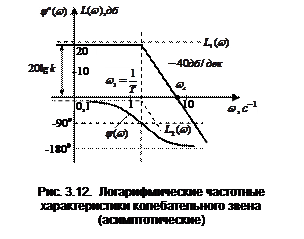
Точные ЛАЧХ колебательного звена отличаются от асимптотической ЛАЧХ. Эти отклонения в значительной степени зависят от коэффициента относительного затухания ξ, входящего в выражение передаточной функции.

Добавляя поправки, соответствующие различным значениям ξ к асимптотической ЛАЧХ, можно получить точные ЛАЧХ.

Если построить семейство кривых (ЛАХ) для одного и того же значения 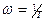и различных значениях ξ, то можно показать, что при значениях 0.35 < ξ < 0.75 расхождение между асимптотической и истинными ЛАЧХ на превышает 3дб, как и в случае апериодического звена.

Поэтому в этом случае можно пользоваться асимптотическими ЛАЧХ. При других значениях асимптотическую ЛАЧХ корректируют с помощью готовых графиков поправок, дающих разность между истинной и асимптотической ЛАЧХ. L(ω) в этом случае строится по расчётным точкам (рис. 3.13).

Если 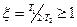, то колебательное звено превращается в апериодическое звено второго порядка, описываемое передаточной функцией (3.28).

Корни характеристического уравнения в данном случае будут равны:

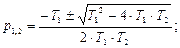
Переходная характеристика описывается уравнением (3.29). Если 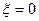, то колебательное звено превращается в консервативное звено.

Логарифмическая фазо-частотная характеристика колебательного звена φ(ω) рассчитывается по формуле:

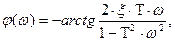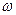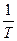
при <

при >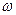

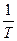
На рис.3.14 представлены эти характеристики при различных значениях коэффициента ξ, из которых видно, что ЛФЧХ колебательного звена изменяется от 0⁰ в области низких частот до 180⁰ в области высоких частот. На частоте сопряжения 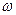₁= 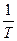сдвиг по фазе равен -90⁰.