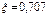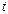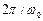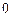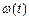Колебательное звено
Колебательным называется звено второго порядка, в котором при получении на входе ступенчатого воздействия, выходная величина стремится к новому установившемуся значению, совершая затухающие колебания.
Переходный процесс такого звена описывается дифференциальным уравнением второго порядка.
 (3.19)
(3.19)
или
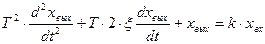 (3.20)
(3.20)
где T1 и T2 – постоянные времени колебательного звена, имеющие размерность времени;
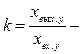 коэффициент усиления (передачи) звена;
коэффициент усиления (передачи) звена;
T – эквивалентная постоянная времени звена
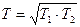 ;
;
 – постоянная безразмерная величина, называемая относительным коэффициентом затухания колебательного звена
– постоянная безразмерная величина, называемая относительным коэффициентом затухания колебательного звена 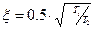 .
.
К колебательным звеньям можно отнести R-L-C цепи, двигатель постоянного тока, электромашинный усилитель, механические элементы, обладающие массой, упругостью и вязким трением и др.
Операторные уравнения колебательного звена:
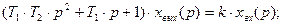
|
|
|
|
|
|
|
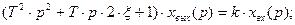
Переходные функции колебательного звена:
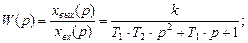

Характеристические уравнения колебательного звена:
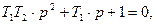
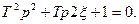
Отсюда корни характеристического уравнения:
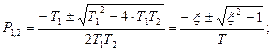
Переходная характеристика колебательного звена при ступенчатом входном воздействии 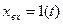 будет описываться следующим уравнением:
будет описываться следующим уравнением:
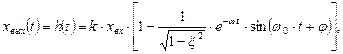
где 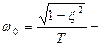 угловая частота собственных колебаний звена;
угловая частота собственных колебаний звена;
|
|
|
|
|
 декремент затухания колебательного звена (чем больше величина α, тем быстрее происходит уменьшение амплитуды колебаний переходной функции);
декремент затухания колебательного звена (чем больше величина α, тем быстрее происходит уменьшение амплитуды колебаний переходной функции);
 – начальная фаза колебаний;
– начальная фаза колебаний;
ξ – относительный коэффициент затухания.
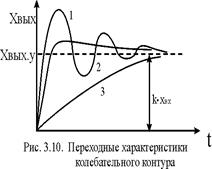
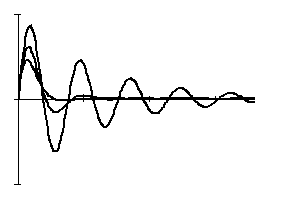
Это выражение характеризует затухающий колебательный процесс (рис. 3.10) с затуханием, определяемым величиной α и частотой ω.
Из выражения видно, что характер переходной функции зависит от коэффициента ξ:
1) При 0 < ξ < 1 – переходная функция имеет вид затухающих колебаний;
2) При ξ = 0 – переходная функция будет представлять собой незатухающие колебания, в данном случае колебательное звено будет называться консервативным и будет иметь передаточную функцию
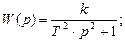
3) При -1 < ξ < 0 – на выходе звена со следующей переходной характеристикой
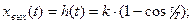
появляются возрастающие по амплитуде колебания;
Звено будет иметь следующую передаточную функцию

т.е. звено будет неустойчивым;
4) При ξ > 1 – переходная функция имеет монотонный характер и колебательное звено превращается в апериодическое звено второго порядка с передаточной функцией
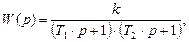 (3.28)
(3.28)
где 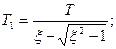

Если  >>1 ,то T2<<T1 и влиянием T2 на переходный процесс можно пренебречь.
>>1 ,то T2<<T1 и влиянием T2 на переходный процесс можно пренебречь.
Импульсная переходная (весовая) функция:
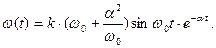

|
|
|
|
|


|
|
 |
Амплитудно-фазовая частотная характеристика
Дата добавления: 2016-03-20; просмотров: 2665;