Логарифмические частотные характеристики САР

При исследовании САУ, амплитудную и фазовую частотные характеристики удобно строить в логарифмических координатах. Это объясняется тем, что:

1) в логарифмических координатах кривизна характеристик изменяется, возникает возможность в подавляющем большинстве практических случаев упрощённо изображать амплитудные частотные характеристики ломаными линиями;

2) удобно строить амплитудные частотные характеристики последовательно соединённых звеньев САУ.

Частотные характеристики, построенные в логарифмическом масштабе, так называемые логарифмические частотные характеристики (ЛЧХ), находят широкое применение при исследовании САУ.

Если уравнение АФХ задано в виде

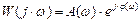
где 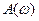– модуль и 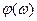– аргумент являются функциями частоты ω, то после логарифмирования правой и левой части уравнения получим

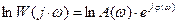
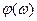Выражения и представляют соответственно уравнения логарифмической амплитудной (ЛАХ) логарифмической фазовой (ЛФХ) частотных характеристик.

Амплитудная частотная характеристика в логарифмических координатах строится обычно в виде зависимости 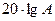от . Фазовая частотная характеристика строится в виде зависимости φ от . Величина 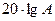обозначается 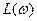. В качестве единицы измерения этой величины используется децибел, равный одной десятой бела. Бел – это единица измерения десятичного логарифма коэффициента усиления мощности сигнала, т. е. 1 бел соответствует усилению мощности в 10 раз, 2 бела – в 100 раз, 3 бела – в 1000 раз и т. д. Т.к. мощность сигнала пропорциональна квадрату амплитуды, а 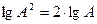, то усиление в белах, выраженное через отношение амплитуд A равно 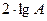. Соответственно, в децибелах оно равно 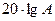. При этом существуют следующие соотношения между

значениями A(ω) и L(ω):

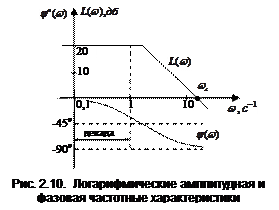
Логарифмическая фазовая частотная характеристика (ЛФЧХ) строится в полулогарифмических координатах, т.е. в виде зависимости 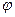от 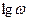, чтобы обе характеристики были связаны одним масштабом по оси абсцисс. Использование логарифмического масштаба на оси ординат фазовой характеристики не имеет смысла, т.к. фазовый сдвиг цепочки звеньев получается просто в виде суммы фазовых сдвигов на отдельных её звеньях.

На оси абсцисс указывается либо значение 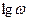, либо, что практически более удобно, значения самой частоты ω (рис. 2.10.). В первом случае единицей приращения 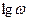является декада, соответствующая изменению частоты в десять раз. Применяется также деление оси абсцисс на октавы. Октава соответствует изменению частоты в два раза (одна октава равна 0.303 декады). При использовании логарифмического масштаба точка, соответствующая ω = 0, находится слева в бесконечности, поэтому логарифмические характеристики строятся не от нулевой частоты, а от частоты малого, но конечного значения ω, которое и откладывается в точке пересечения координатных осей.

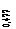
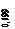
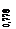
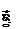
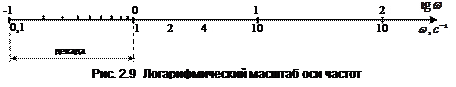
Контрольные вопросы для самопроверки

1. Какова стандартная форма записи линейных уравнений в системах автоматического регулирования?

2. Что дает применение прямого преобразования Лапласа при математическом описании САР?

3. Что такое передаточная функция элементов и систем автоматического регулирования, и как её получить по дифференциальным уравнениям?

4. Каким образом можно получить уравнение статики из уравнения динамики системы?

5. Составить дифференциальные уравнения цепи, состоящей из последовательно соединенных активного сопротивления R, индуктивности L и емкости C (R-L, R-C, R-L-C) при подаче на её вход постоянного по величине напряжения U. Вывести выражения для передаточной функции этих цепей.

6. В чем заключается сущность, и как получается выражение для передаточного коэффициента элемента или системы автоматического регулирования?

7. Как получить характеристическое уравнение звена или САР в целом? Для каких цепей составляется и решается характеристическое уравнение?

8. Каким образом определяется амплитудная и фазовая частотные характеристики звеньев и САР?

9. В чем заключается сущность частотных характеристик звеньев и САР?

10. Дать понятие и объяснить логарифмические амплитудную и фазовую частотные характеристики.

11. Каким образом можно построить логарифмические амплитудную и фазовую частотные характеристики?

12. В чем сущность линеаризации дифференциального уравнения элементов, и как её практически осуществлять?

13. Какой режим устанавливается в линейной системе при гармоническом воздействии, и какими параметрами он характеризуется?

14. Как по частотным характеристикам разомкнутой системы определить её частотные характеристики в замкнутом состоянии?

15. Какие частотные характеристики вы знаете и в чем их физический смысл?