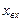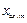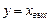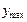Частотные характеристики САУ

Рассмотрим понятие о частотных характеристиках, которые широко используются при анализе САУ. Это понятие применимо как к отдельному звену, так и к системе в целом. Частотные характеристики описывают установившиеся вынужденные колебания на выходе звена, вызванные гармоническим воздействием на входе.

Рассмотрим такой режим.

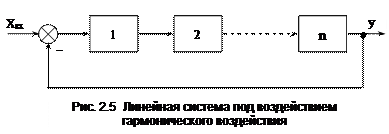
Пусть на вход линейной разомкнутой системы, изображенной на рис. 2.5, подано гармоническое воздействие

,

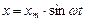или в символической форме

,

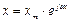где 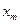– амплитуда,

ω – угловая частота этого воздействия.

По истечении некоторого времени после подачи такого воздействия, после окончания переходного процесса, на выходе системы установится также гармоническое изменение выходной величины, но с другими амплитудой и фазой.

Следовательно, в установившемся режиме выходная величина системы будет

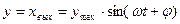
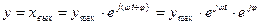
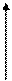
При фиксированной амплитуде входных колебаний амплитуда и фаза установившихся колебаний на выходе системы зависят от частоты входного возмущающего воздействия. Если постепенно увеличивать от нуля частоту колебаний и определять установившиеся значения амплитуды и фазы выходных колебаний для разных частот, то можно получить зависимости от частоты отношения амплитуд 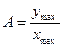и сдвига фаз φ(ω) выходных и входных установившихся колебаний. Эти зависимости называются соответственно: A(ω) – амплитудной частотной характеристикой (АЧХ) и φ(ω) – фазовой частотной характеристикой (ФЧХ).

Рассмотрим основные понятия, связанные с частотными характеристиками.

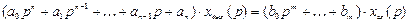
Если подать на вход этой системы гармоническое возмущение

,

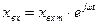на выходе будем иметь

,

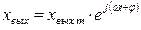Известно, что

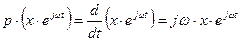Аналогично

и т.д. Поэтому операторные уравнения для разомкнутой системы можно записать в виде

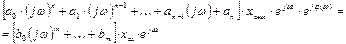
Сокращая на 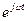, получим выражение, которое позволяет определить при заданном периодическом возмущении на входе изменение амплитуды и фазы на выходе системы (звена) в зависимости от частоты ω.

Это выражение представляет собой передаточную функцию звена или разомкнутой системы, в которой вместо p подставлено (jω), т.е.

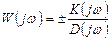
Выражение W(jω) называют комплексным коэффициентом передачи (усиления) или комплексной частотной функцией разомкнутой системы. При ω=0 получим выражение для коэффициента передачи системы.

Эту функцию можно представить в декартовых координатах на комплексной плоскости

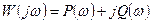
или в полярных координатах

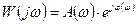
Отсюда имеем для АЧХ и ФЧХ

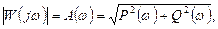
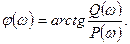
При некотором фиксированном значении частоты ω входного сигнала комплексная частотная функция W(jω) будет представлять собой вектор с амплитудой A(ω) и аргументом φ(ω) (рис 2.7.). Для различных ω будут различные А(ω) и φ(ω). Если изменять ω от 0 до бесконечности, можно получить множество различных векторов. Огибающая, проведенная через концы этих векторов называется годографом вектора комплексной частотной характеристики. Кривая называется также амплитудно-фазовой частотной характеристикой (АФЧХ). Иногда выражение, соответствующее W(jω) называют частотной передаточной функцией.

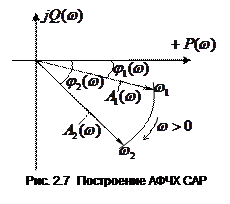
Следовательно, АФЧХ называется линия, соединяющая концы радиусов-векторов, длины которых равны отношению амплитуд выходного и входного сигналов, а угол, образуемый вектором с положительным направлением вещественной оси, равен разности фаз выходного и входного сигналов для частот, изменяющихся от 0 до ∞.

Примерный вид частотных характеристик можно представить на рис. 2.7.

В соответствии с преобразованием Фурье АФЧХ должна строиться при изменении частот от -∞ до +∞. Но ветвь характеристики, получающаяся при изменении частот от 0 до -∞ можно получить как зеркальное отображение W(jω) относительно вещественной оси ветви W(jω), полученной при изменении ω от +∞ до 0. Поэтому при характеристических расчетах достаточно ограничится только положительными значениями ω.

Между переходной функцией и АФЧХ динамической системы также существует определенная связь, т.к. они получаются из одного и того же дифференциального уравнения. В первом случае на вход подается воздействие типа единичного скачка, во втором случае – синусоидальное возмущение. Эта связь дает возможность по АФХ системы построить её переходную функцию, не решая уравнения. Для этого обычно используется вещественная часть частотной АФХ. По графику переходной функции можно получить кривую переходного процесса при ступенчатом воздействии, умножив все координаты переходной функции на входную величину.

По имеющейся переходной функции, полученной, например, экспериментальным путем, можно построить АФХ. Это обычно делается при автоматизации сложных технологических объектов, у которых расчетным путем нельзя получить ни переходную функцию, ни частотные характеристики.