Реальные интегрирующие звенья или интегрирующие звенья с замедлением

Реальные интегрирующие звенья обычно обладают определённой инерционностью, вследствие чего, их выходная величина при подаче на вход входного сигнала изменяется с определённым замедлением.

Исходное дифференциальное уравнение интегрирующего звена с замедлением будет иметь вид:

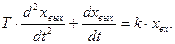
или в операторном виде:

,

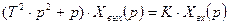или

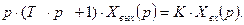
Изображение выходной величины:

Если перейти от изображения к оригиналу при подаче на вход ступенчатого воздействия 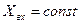и при нулевых начальных условиях, получим выражение переходной функции:

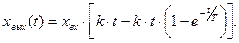
Принимая 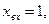получим уравнение переходной функции, график которой приведён на рисунке. 3.26.

Импульсная весовая переходная функция, т.е. реакция звена на единичный импульс:

Передаточная функция имеет следующий вид:

.

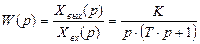Уравнение амплитудно-фазовой характеристики:

.

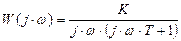Если определить вещественную и мнимую части, то получим:

Амплитудная частотная характеристика:

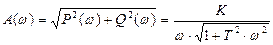
Фазовая частотная характеристика:

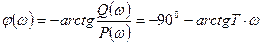
Амплитудная и фазовая частотные характеристики звена представлены на рис. 3.27.