Звенья второго порядка
Звеном второго порядка называется звено, связь между выходной и входной величиной которого определяется линейным дифференциальным уравнением второго порядка вида
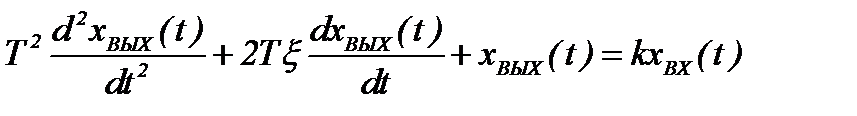 , (2.60)
, (2.60)
где Т – постоянная времени ; ξ – относительный коэффициент затухания (демпфирования).
Применяя к (2.60) преобразование Лапласа при нулевых начальных условиях, получим операторное уравнение
 . (2.61) . (2.61)
|
В зависимости от вида корней характеристического уравнения инерционное звено второго порядка может иметь различные переходные характеристики. Это позволяет установить три разновидности звена – апериодическое, колебательное и консервативное.
При единичном входном воздействии для случая вещественных различных корней р1 и р2 по уравнению (2.61) получим переходную функцию (ξ≥1):
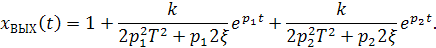
В случае вещественных корней апериодическое звено второго порядка эквивалентно последовательному соединению двух инерционных звеньев первого порядка, поэтому передаточная функция может быть записана в виде

По выражению W(p) после замены р на jω получим частотную функцию W(jω) апериодического звена второго порядка, которая определяет частотные характеристики звена.
Дата добавления: 2016-04-11; просмотров: 1477;
