Колебательное звено. Если корни уравнения (2.61) будут комплексными, то инерционное звено второго порядка станет колебательным (ξ<1).

Если корни уравнения (2.61) будут комплексными, то инерционное звено второго порядка станет колебательным (ξ<1).

, (2.62)

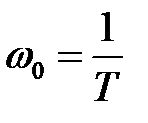где .

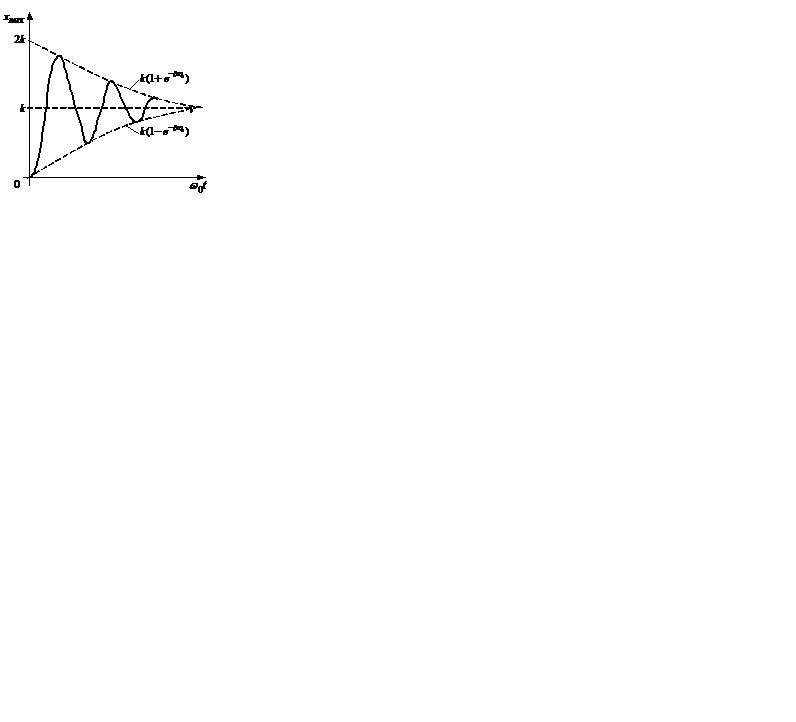График переходной функции колебательного звена показан на рисунке 2.19. Примерами колебательного звена могут служить упругая механическая система с существенным влиянием массы, электрический колебательный контур и т.д.

По уравнениям (2.61) определяется передаточная функция инерционного звена

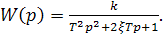(2.63)

На основании W(p) получим выражение для амплитудно-фазовой характеристики W(jω)

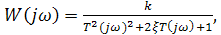(2.64)

Рисунок 2.19

по которой при различных значениях коэффициента затухания можно построить серию частотных характеристик колебательного звена (рисунок 2.20). Как видно из рисунка, годограф частотной характеристики проходит через два квадранта – IY и III – пересекает мнимую ось при ωТ=1, когда в выражении (2.63) 1+(jωT)² =0. При этом .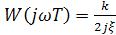

С уменьшением ξ петля, очерченная годографом, увеличивается, и при ξ=0 характеристика вырождается в две полупрямые: 1 – от W(j ωT)=k до W(j ωT)→∞ при 0 < ωT<1 до 2 – от W(j ωT)→-∞ до W(j ωT)=0 при 1< ωT<∞.

Амплитудно-частотная и фазо-частотная характеристики колебательного звена выражаются уравнениям

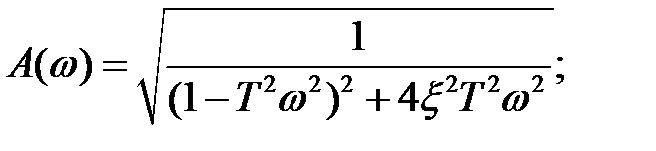(2.65)

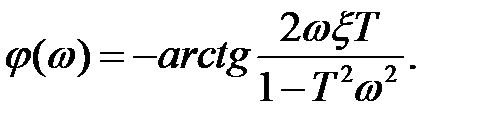(2.66)

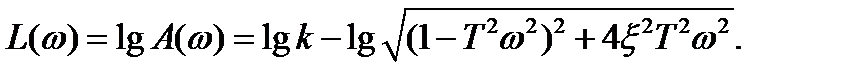Логарифмическая амплитудно-фазовая характеристика колебательного звена описывается уравнением

(2.67)

Вблизи точки резонанса (ωT=1) эта характеристика сильно зависит от коэффициента затухания ξ. С удалением от резонансной частоты характеристика практически перестаёт зависеть от ξ.

Для колебательных звеньев пользуются асимптотическими характеристиками

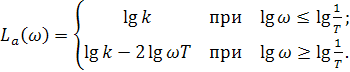(2.68)

Поправка к асимптотической характеристике

зависит от коэффициента затухания ξ. Графики L(ω) и φ(ω) для различных ξ показаны на рисунке 2.21. У колебательных звеньев возникает всплеск при .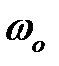

Рисунок 2.21