Инерционно-форсирующее (упругое) звено
Это звено, у которого связь между выходным и входным сигналами выражается уравнением вида:
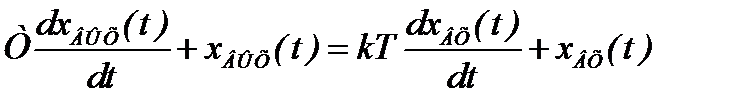 , (2.50)
, (2.50)
где Т – постоянная времени;
k – коэффициент усиления.
Существенным параметром инерционно-форсирующего звена является коэффициент усиления. Если k<1, то звено по своим свойствам приближается к интегрирующему и инерционному звеньям. Если k>1, то звено ближе к дифференцирующему и инерционно-дифференцирующему звеньям.
Инерционно-форсирующее звено наряду с реальным дифференцирующим звеном применяется как средство для корректирования, улучшения переходных процессов.
Применяя к (2.50) преобразование Лапласа при нулевых начальных условиях, получим операторное уравнение
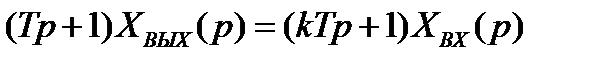 . (2.51)
. (2.51)
Переходная функция звена
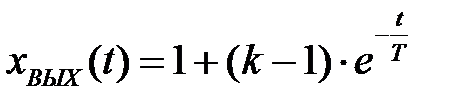 . (2.52)
. (2.52)
Переходная характеристика инерционно-форсирующего звена построенная по (2.52) при единичном входном воздействии изображены на рисунке 2.16 при [k>1 – а); при k<1 – б)].
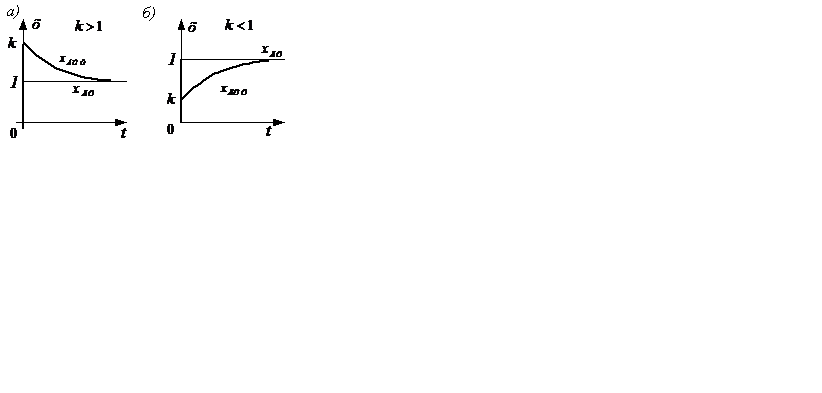
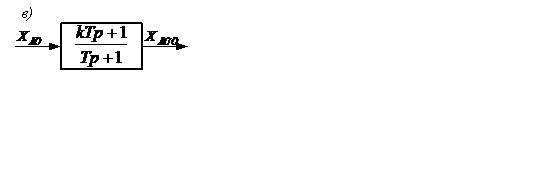
Рисунок 2.16 – Переходные характеристики а) ; б) и
изображение в) на структурных схемах
Передаточная функция инерционно-форсирующего звена на основании (2.51) запишется как
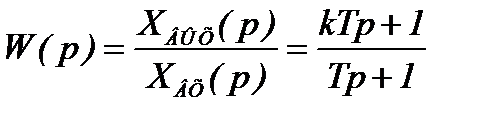 . (2.53)
. (2.53)
Комплексный коэффициент передачи получится путём замены pна jω
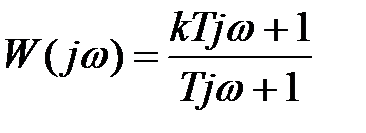 , (2.54)
, (2.54)
или
 (2.55)
(2.55)
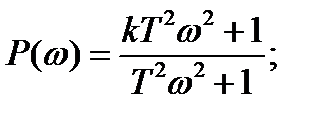
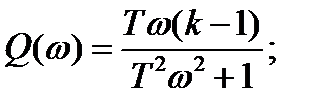 где
где
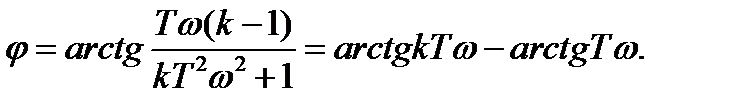
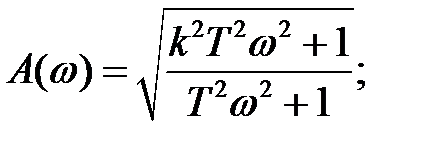
(2.56)
На рисунке 2.17 построены годографы W(jω) и частотные характеристики инерционно-форсирующего звена при k>1 (а,б,в) и k<1 (г,д,в).

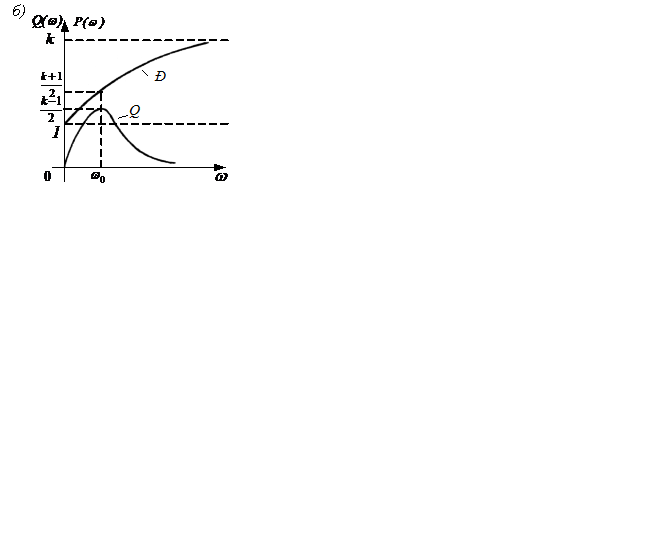
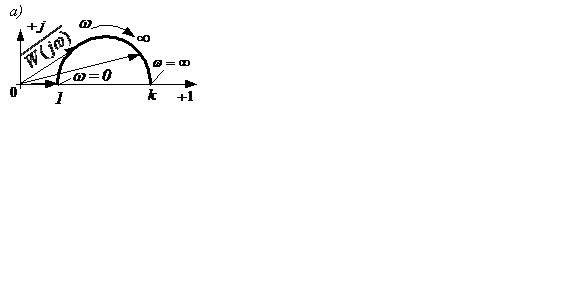
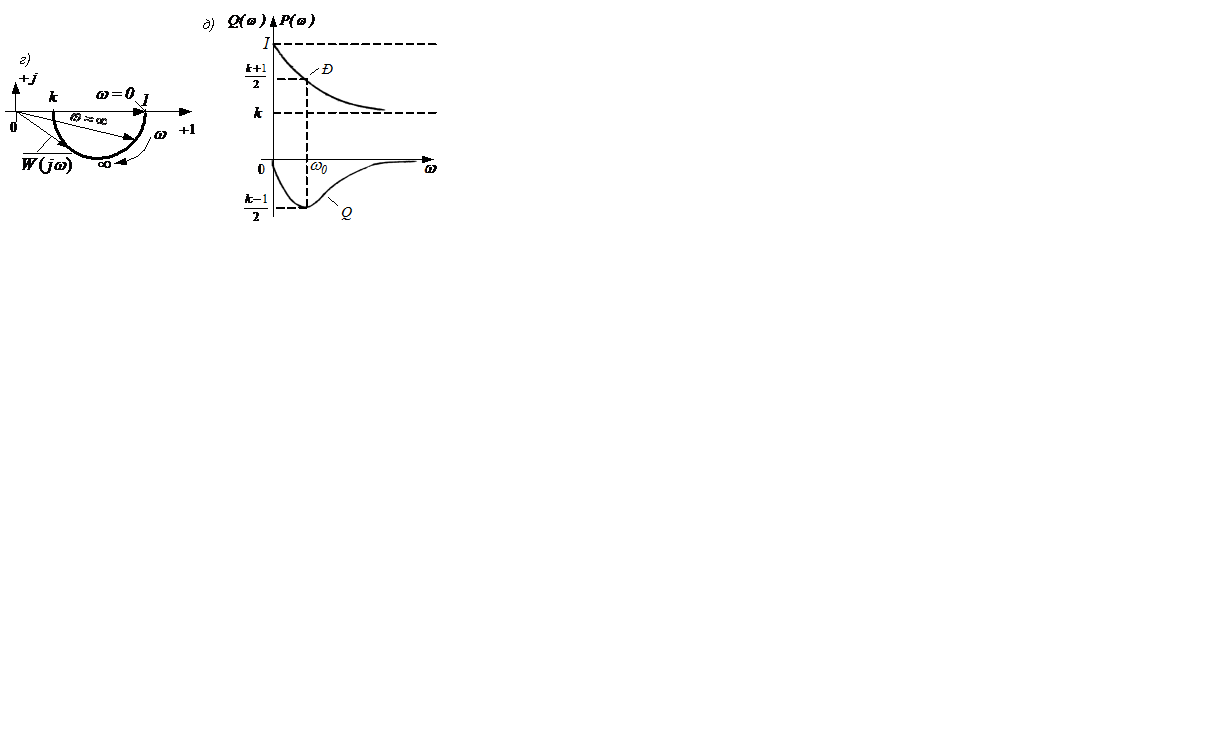
Рисунок 2.17
Логарифмическая амплитудно-фазовая характеристика описывается уравнением
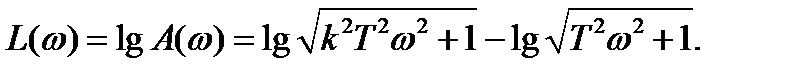 (2.58)
(2.58)
Асимптотические характеристики в зависимости от величины k выражаются различно:
если k>1
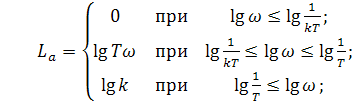 (2.59)
(2.59)
если k<1
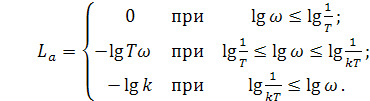 (2.60)
(2.60)
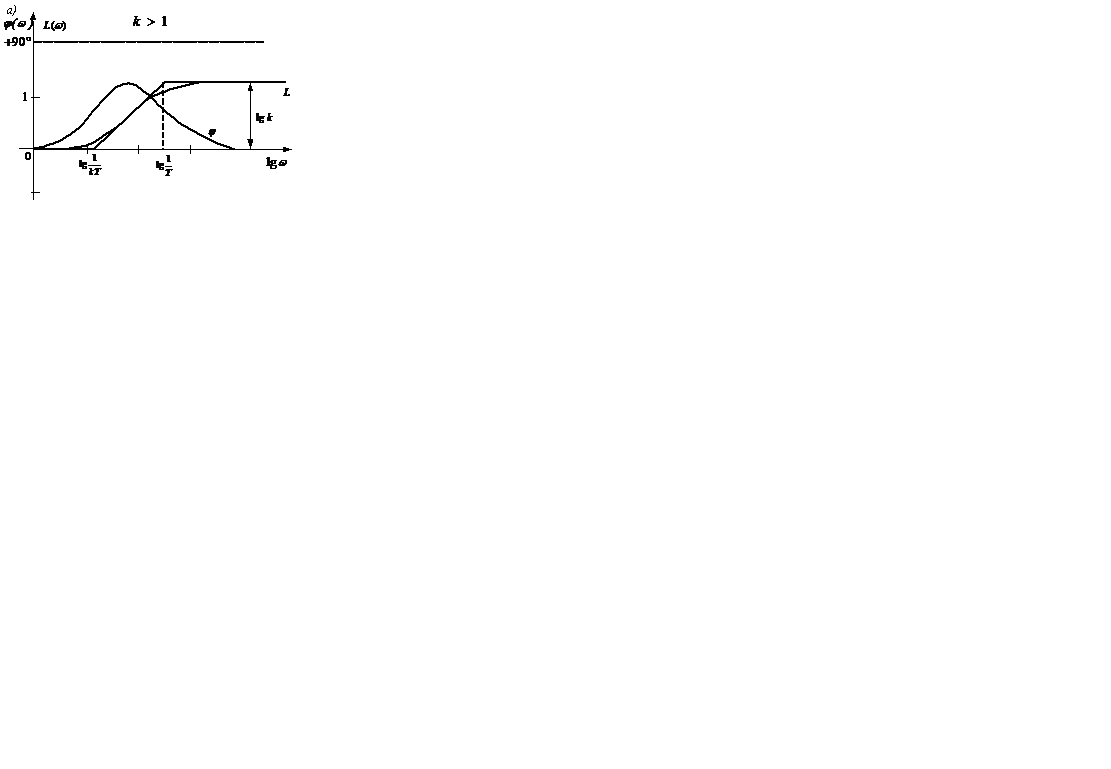
Логарифмические амплитудно – и фазо-частотные характеристики инерционно-форсирующего звена изображены на рисунке 2.18 (а при k >1, б при k<1).
 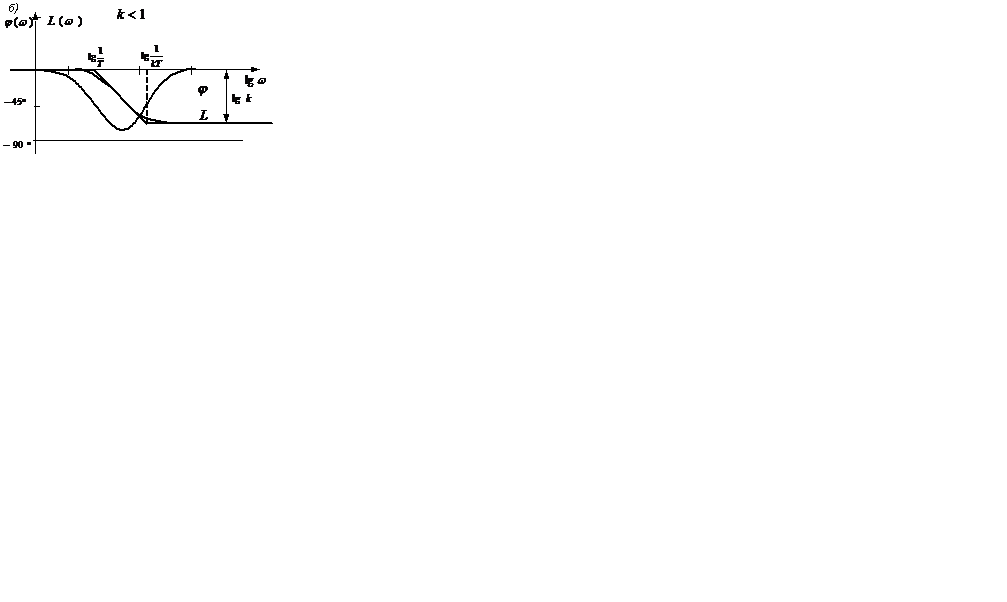
|
Рисунок 2.18
Дата добавления: 2016-04-11; просмотров: 917;
