Консервативное звено

Уравнение динамики консервативного вена имеет вид

(2.69)

где Т – постоянная времени;

k– коэффициент усиления (или передачи).

Переходный процесс такого звена показан на рисунке 2.22.

Рисунок 2.22

Рисунок 2.23

Консервативное звено – частный случай звена второго порядка, когда отсутствует демпфирование (ξ=0). Применяя к (2.69) преобразование Лапласа при нулевых начальных условиях, получим операторное уравнение

.

Передаточная функция консервативного звена

(2.70) На основании (2.70) получим частотную функцию

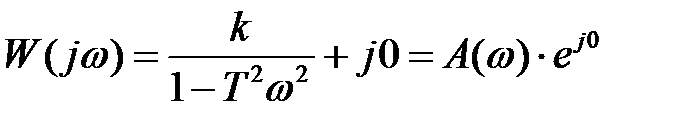, (2.71)

где

(2.72)

Логарифмическая амплитудно-частотная характеристика имеет разрыв при ω=ω₀ (рисунок 2.23), что свидетельствует о возникновении незатухающих колебаний с этой частотой. Логарифмическая амплитудно-частотная характеристика может быть представлена в виде двух отрезков прямых линий. Одна линия уходит при lgω₀≤lgω<∞ вправо от точки lgω₀под углом -2 лог/дек; вторая линия при -∞<lgω≤lgω₀ совпадает с линией lgkпраллельной оси абсцисс.

Фазо-частотная характеристика определяет скачкообразное изменение фазы при ω=ω₀ от нуля до -180° (рисунок 2.23). Звено является минимально-фазовым.

Примером консервативного звена может служит идеальный пассивный четырёхполюсник, состоящий из Lи С (при отсутствии омического сопротивле- ния цепи), и другие элементы, если уравнения их динамики имеют вид уравнения (2.69).