Последовательное соединение звеньев
Это такое соединение, когда выходная переменная каждого предыдущего звена является входным воздействием для последующего звена (и только для него одного) (рисунок 3.1).
Рисунок – 3.1 Последовательное соединение
Так как для каждого звена
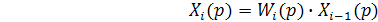 , (3.1)
, (3.1)
то, составив такие уравнения для всех звеньев и исключив из них все промежуточные переменные, кроме входной величины 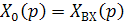 и выходной величины
и выходной величины 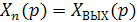 , получаем
, получаем
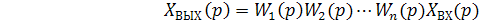 . (3.2)
. (3.2)
Таким образом, передаточная функция системы последовательно соединённых звеньев
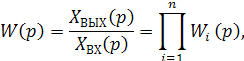
(3.3)
то есть равна произведению передаточных функций отдельных звеньев.
Выражение (3.3) справедливо и для обратных передаточных функций последовательно соединённых звеньев:
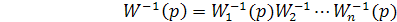 . (3.4)
. (3.4)
Переходя к АФЧХ и подставляя p=jω, получим:
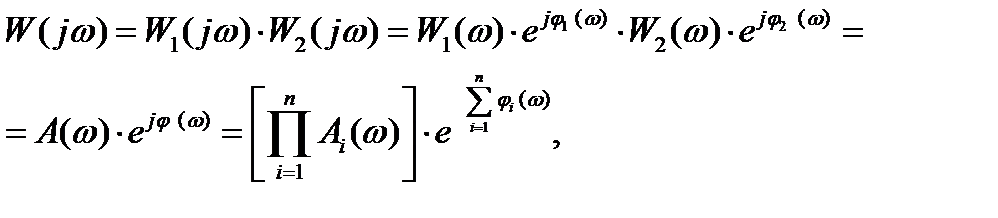 (3.5)
(3.5)
При этом модули комплексных коэффициентов перемножаются, а аргументы складываются
A(ω) = A1(ω)·A2(ω,)·…· Аn(ω),
φ(ω) = φ1(ω) + φ2(ω)+…+φn(ω). (3.6)
При последовательном соединении звеньев логарифмические амплитудно-частотные и фазочастотные характеристики отдельных звеньев складываются:
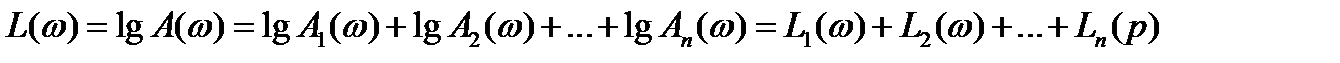 ,
,
φ(ω) = φ1(ω) + φ2(ω)+…+φn(ω). (3.7)
При последовательном соединении минимально-фазовых звеньев полученная система также будет минимально-фазовой, т.е. её передаточная функция не будет иметь ни нулей, ни полюсов в правой полуплоскости. Действительно, если каждый из сомножителей произведения (3.5) не имеет ни нулей, ни полюсов в правой полуплоскости р, то то же можно сказать и об их произведении. Аналогично можно показать, что если хотя бы одно из последовательно соединённых звеньев неминимально-фазовое или неустойчивое, то и вся система будет неминимальнофазовой или неустойчивой.
Дата добавления: 2016-04-11; просмотров: 797;
