НеопределеннЫЙ интеграл
Функция 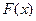 называется первообразнойфункции
называется первообразнойфункции 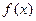 , если выполняется условие:
, если выполняется условие: 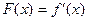 .
.
Теорема.Если 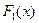 и
и 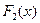 две первообразные одной и той же функции
две первообразные одной и той же функции 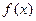 , то они отличаются не более, чем на константу, то есть
, то они отличаются не более, чем на константу, то есть 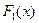
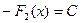 .
.
Следствие. Если 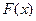 - одна из первообразных функции
- одна из первообразных функции 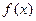 , то любая другая первообразная имеет вид
, то любая другая первообразная имеет вид 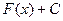 .
.
Совокупность всех первообразных функции 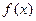 называется неопределенным интеграломот
называется неопределенным интеграломот 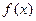 и обозначается
и обозначается 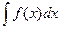 , здесь
, здесь 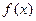 называется подынтегральной функцией, а
называется подынтегральной функцией, а 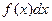 - подынтегральным выражением.
- подынтегральным выражением.
Таким образом, окончательно 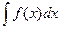 =
= 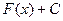 .
.
Свойства неопределенного интеграла.
I. Свойство о связи интегрирования и дифференцирования:
1. 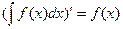 ; 2.
; 2. 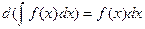 ; 3.
; 3. 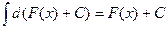 .
.
Таким образом, интегрирование и дифференцирование взаимнообратные операции. Встречаясь последовательно в некотором математическом выражении они взаимно уничтожаются.
II. Свойство линейности: 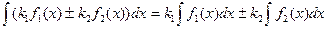 .
.
III. Свойство инвариантности: формула интегрирования не изменится при замене переменной на некоторую дифференцируемую функцию этой переменной. Следствие: 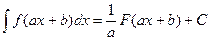 .
.
Таблица ОСНОВНЫХ неопределенных интегралов
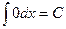 ; ;
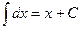 ; ;
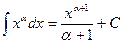 , при , при 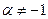 ; ;
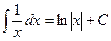 ; ;
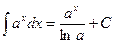 ; ;
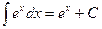 ; ;
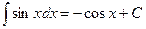 ; ;
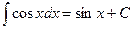 ; ;
| 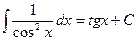 ; ;
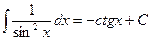 ; ;
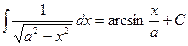 ; ;
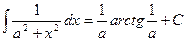 ; ;
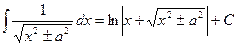 ; ;
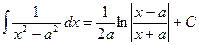 . .
|
Дата добавления: 2016-03-22; просмотров: 615;
