Элементарное исследование функции
Исследовать функцию – значит охарактеризовать ее поведение при изменении независимой переменной. Для элементарного исследования необходимо:
· найти область определения функции;
· определить нули функции, точки пересечения графика с осями координат;
· исследовать на четность/нечетность;
· исследовать на периодичность.
Область определения – это множество всех значений аргументов функции, при которых она имеет смысл.
Нули функции – это те значения ее аргумента, при которых функция равна нулю.
Функция называется четной, если она задана на симметричном относительно начала координат промежутке и если f(-x) = f(x), и нечетной если f(-x) =-f(x). Для того чтобы установить четность или нечетность функции, требуется определить, является ли область определения функции интервалом, симметричным относительно начала координат, и выполняется ли одно из условий: f(-x) = f(x) или f(-x) = -f(x). Если функция не является четной и не является нечетной, то она называется функцией общего вида. График четной функции симметричен относительно оси ординат. График нечетной функции симметричен относительно начала координат.
Функция называется периодической с периодом Т, если f(x) = f(x + Тп), n 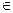 Z.
Z.
ПРДЕЛ ФУНКЦИИ
Число А называется пределом функции 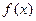 в точке
в точке 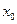 , если при сколь угодно близком приближении аргумента
, если при сколь угодно близком приближении аргумента 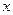 к значению
к значению 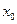 соответствующие значения функции сколь угодно близко приближаются к значению А. Обозначается:
соответствующие значения функции сколь угодно близко приближаются к значению А. Обозначается: 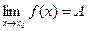 .
.
Число А называется правым (левым) пределом функции 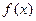 в точке
в точке 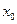 , если при сколь угодно близком приближении аргумента
, если при сколь угодно близком приближении аргумента 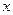 к значению
к значению 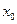 справа (слева) соответствующие значения функции сколь угодно близко приближаются к значению А. Обозначаются:
справа (слева) соответствующие значения функции сколь угодно близко приближаются к значению А. Обозначаются: 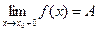 – правый предел,
– правый предел, 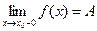 – левый предел.
– левый предел.
Теорема. Функция имеет предел в точке 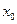 тогда и только тогда, когда в этой точке существуют и равны между собой односторонние пределы функции. В этом случае значение предела совпадает со значением односторонних пределов.
тогда и только тогда, когда в этой точке существуют и равны между собой односторонние пределы функции. В этом случае значение предела совпадает со значением односторонних пределов.
Число А называется пределом функции 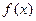 на бесконечности, если при неограниченном увеличении аргумента
на бесконечности, если при неограниченном увеличении аргумента 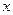 соответствующие значения функции сколь угодно близко приближаются к значению А. Обозначается:
соответствующие значения функции сколь угодно близко приближаются к значению А. Обозначается: 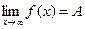 .
.
Справедливы следующие свойства пределов функции:
1. Если предел функции существует, то он единственный.
2. Предел постоянной величины равен самой постоянной.
3. Предел суммы (разности) функций равен сумме (разности) пределов функций.
4. Предел произведения функций равен произведению пределов функций.
5. Предел отношения функций равен отношению пределов функций.
При вычислении пределов функции используются замечательные пределы:
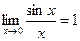 ;
; 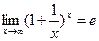 .
.
Дата добавления: 2016-03-22; просмотров: 938;
