Числовая последовательность
Если каждому числу п из множества натуральных чисел поставлено в соответствие некоторое действительное число 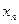 , то множество действительных чисел
, то множество действительных чисел 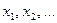 называется числовой последовательностью. Обозначается: Х={
называется числовой последовательностью. Обозначается: Х={ 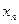 }.
}.
Число а называется пределом числовой последовательности { 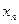 } если для любого положительного числа
} если для любого положительного числа 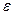 найдется номер N , начиная с которого выполняется условие
найдется номер N , начиная с которого выполняется условие 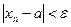 . Обозначается:
. Обозначается: 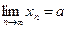 .
.
Если числовая последовательность имеет конечный предел, то она сходится. Если предел бесконечен или не существует, то последовательность расходится.
Последовательность называется бесконечно малой если ее предел равен нулю. Последовательность называется бесконечно большой если ее предел равен бесконечности. Бесконечно малые и бесконечно большие последовательности являются взаимообратными.
Свойства бесконечно малых:
1. Сумма бесконечно малых является бесконечно малой.
2. Произведение бесконечно малых является бесконечно малой.
3. Произведение бесконечно малой на величину ограниченную является бесконечно малой.
Алгебрическими композициями последовательностей { 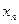 } и {
} и { 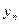 } называются последовательности {zn} вида {хп + уп},{хп – уп}, { хп
} называются последовательности {zn} вида {хп + уп},{хп – уп}, { хп 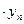 }, { хп / уп}. Если последовательности {хп}и {уп}имеют конечные пределы a и b то последовательность {zn}имеет пределы а + b, а – b, а
}, { хп / уп}. Если последовательности {хп}и {уп}имеют конечные пределы a и b то последовательность {zn}имеет пределы а + b, а – b, а 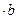 , a / b соответственно.
, a / b соответственно.
В случае когда последовательности {хп},{уп}являются бесконечно большими или бесконечно малыми, могут возникать неопределенности вида 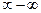 (разность бесконечно больших),
(разность бесконечно больших), 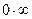 (произведение бесконечно малой и бесконечно большой),
(произведение бесконечно малой и бесконечно большой), 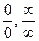 (отношения бесконечно малых и бесконечно больших),
(отношения бесконечно малых и бесконечно больших), 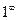 .
.
Дата добавления: 2016-03-22; просмотров: 535;
