МОНОТОННОСТЬ ФУНКЦИИ

Функция y=f(x) на интервале (a, b) называется:

· возрастающей, если для любых точек этого интервала 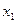< 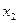выполняется условие ;

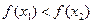· убывающей, если для любых точек этого интервала 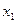< 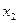выполняется условие ;

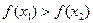· постоянной, если для любых точек этого интервала 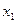< 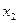выполняется условие .

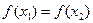Перечисленные функции называются монотонными.

Достаточный признак монотонности. Если в каждой точке интервала (a, b):

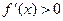· , то функция на этом интервале возрастает;

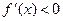· , то функция на этом интервале убывает;

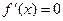· , то функция на этом интервале постоянна.

ЭКСТРЕМУМЫ ФУНКЦИИ

Значение f(x₀) называется локальным максимумом (локальным минимумом) функции у = f(x), если в некоторой окрестности точки x₀ для любого x выполняется условие f(x₀) > f(x) (f(x₀)<f(x)). Точка x₀ называется точкой максимума (минимума) функции. Локальные максимумы и минимумы функции называются экстремумами функции, а точки максимума или минимума – точками экстремуме

Теорема(необходимое условие локального экстремума). Если функция у = f(x) имеет в точке х₀ локальный экстремум, то производная f'(x) в этой точке обращается в нуль или не существует.

Точки, в которых f'(x) = 0 или f'(x) не существует, называются критическими. Экстремум в таких точках может быть, а может и не быть.

Теорема (достаточное условие экстремума). Пусть х₀ – критическая точка функции у = f(x); если при переходе через точку х₀ слева направо производная f'(x) меняет знак с плюса на минус (с минуса на плюс), то функция f(x) в точке х₀ имеет локальный мак (локальный минимум); если же производная f'(x) не меняет знак в окрестности точки х₀, то данная функция не имеет в точке х₀ локального экстремума.