Функции одной переменной

Если некоторому числу х из множества X поставлено в соответствие согласно некоторому правилу f единственное число у = f(x), то говорят, а множестве X задана функциональная зависимость или функц2ия. При этом величину у называют зависимой переменной, значением функции а величину х – независимой переменной или аргументом функции. Множество X называют областью определения функции и обозначают D(f) = X, а множество чисел у=f(x) объединяют в множество У и называют множеством значений функции. Это множество обозначают также E(f) = У. Наиболее распространены табличный, графический и аналитический способы задания функции.

Основные элементарные функции:

· степенные;

· показательные;

· логарифмические;

· тригонометрические;

· обратные тригонометрические.

Все функции, полученные в результате выполнения конечного числа арифметических действий и суперпозиций над основными элементарными функциями, называются элементарными функциями.

Элементарные функции подразделяются на: рациональные, иррациональные и трансцендентные. Рациональные функции представляются в виде алгебраических многочленов или в виде отношения алгебраических многочленов (т.е. являются дробно-рациональными). Иррациональные функции получены в результате выполнения действий над степенными функциями как с целыми, так и дробными показателями. Трансцендентные – это все остальные функции.

Если на множестве D определена функция 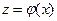с множеством значений Е, а на множестве Е определена функция 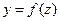, то функция 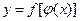называется сложной функцией аргумента х, а переменная z называется промежуточным аргументом сложной функции.