Прямая на плоскости и в пространстве
Прямая на плоскости однозначно проходит через две заданные точки 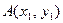 и
и 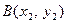 . Основными видами уравнения прямой на плоскости является:
. Основными видами уравнения прямой на плоскости является:
1) уравнение прямой, проходящей через две заданные точки: 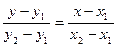 ;
;
2) уравнение прямой с угловым коэффициентом: 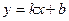 , где
, где 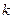 – угловой коэффициент, равный по величине тангенсу угла наклона прямой к оси абсцисс,
– угловой коэффициент, равный по величине тангенсу угла наклона прямой к оси абсцисс, 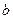 – отрезок, отсекаемый прямой на оси ординат;
– отрезок, отсекаемый прямой на оси ординат;
3) уравнением прямой с угловым коэффициентом 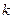 и проходящей через заданную точку
и проходящей через заданную точку 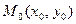 :
: 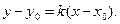
Если две прямые параллельны, то их угловые коэффициенты равны 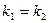 . Если две прямые взаимно перпендикулярны, то их угловые коэффициенты взаимообратные с противоположным знаком
. Если две прямые взаимно перпендикулярны, то их угловые коэффициенты взаимообратные с противоположным знаком 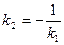 .
.
Прямая в пространстве проходит через две заданные точки 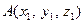 и
и 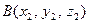 . Уравнение прямой имеет вид:
. Уравнение прямой имеет вид: 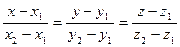 .
.
Прямая в пространстве однозначно проходит через точку 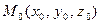 параллельно вектору
параллельно вектору 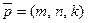 , который называется направляющим. Уравнение прямой имеет вид:
, который называется направляющим. Уравнение прямой имеет вид: 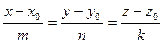 .
.
ПЛОСКОСТЬ
Плоскость однозначно проходит через три заданные точки 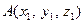 ,
, 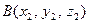 и
и 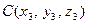 . В этом случае уравнение плоскости имеет вид:
. В этом случае уравнение плоскости имеет вид:
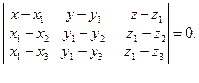
Плоскость однозначно проходит через точку 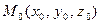 перпендикулярно вектору
перпендикулярно вектору 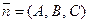 , который называется нормальным. В этом случае уравнение плоскости имеет вид:
, который называется нормальным. В этом случае уравнение плоскости имеет вид: 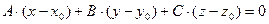 .
.
Общим уравнением плоскости называется уравнение вида:
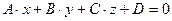 .
.
Дата добавления: 2016-03-22; просмотров: 494;
