Зависимость между 3-мя упругими постоянными G, Е, μ.
Между упругими постоянными существует следующая зависимость: 
КРУЧЕНИЕ.
Построение эпюр крутящих элементов методом сечений.
Крутящий момент Mкв сечении равен сумме моментов слева или справа от сечения.
Правило знаков: Крутящий момент (Mк) считается положительным если окажется, что при взгляде на сечение со стороны нормали момент направлен против часовой стрелки.
Пример 1. Дано: М1 =1кН∙м; М2=2кН∙м; М3= 3кН∙м

| сеч. 1: Мк=0 сеч. 2: Мк= - М1 = - 1 кН·м сеч. 3: Мк= - М1 - М2 = - 1 – 2 = - 3 кН·м сеч. 4: Мк= - 1 – 2 + 3 = 0 |
Связь между крутящим моментом, мощностью и числом оборотов
W=Мк∙ω=Мк ∙π∙n/30 (кГ∙м/сек),
где ω – угловая скорость, n – число оборотов в сек..

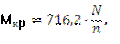
 –мощность, л/с
–мощность, л/с
 (кГс∙м).
(кГс∙м).
 –мощность, кВт (киловатт)
–мощность, кВт (киловатт)
М кр=9,736∙N/n , (кН∙м)
где 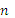 – число оборотов в минуту.
– число оборотов в минуту.
1л/с=0,736кВт.
Определение напряжений и деформации при кручении круглого стрежня.
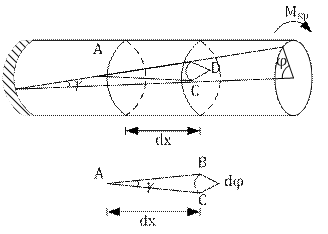
При кручении круглого стержня замечаем:
1) При деформации поперечные сечения не искривляются, а остаются плоскими.
2) Расстояние между поперечными сечениями не изменяются.
3) Радиусы при деформации не искривляются.
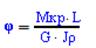 -угол поворота в радианах. -угол поворота в радианах.
 -угол поворота в градусах.
Jρ –полярный момент инерции. -угол поворота в градусах.
Jρ –полярный момент инерции.
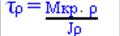 - касательное напряжение на расстоянии ρ от центра
τmax = Мкр ∙r/ Jρ - касательное напряжение на расстоянии ρ от центра
τmax = Мкр ∙r/ Jρ
| 
|
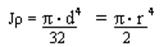 – полярный момент инерции круга
– полярный момент инерции круга
Wρ= Jρ/ r – полярный момент сопротивления
Wρ= π∙d4/ 16 - полярный момент сопротивления круга.
Mк/ Wρ ≤[τ] – проверка прочности при кручении.
Mк/ Wρ ≤ Rsпроверка прочности при срезе,
где 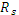 - расчетное сопротивление на срез.
- расчетное сопротивление на срез.
Жесткость при кручении проверяется: 
где 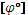 - допускаемый угол поворота на длине равной единице.
- допускаемый угол поворота на длине равной единице.
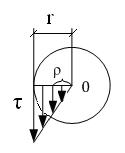
Рассмотрим напряжения в круглом стержне:
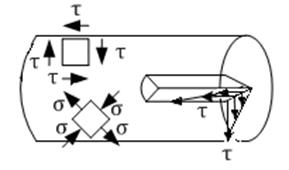
| 1) На основании закона парности касательных напряжений в стержне при кручении появляются касательные напряжения, направленные вдоль оси сечения. 2) Под углом 45°в стержне возникают нормальные напряжения, при чем: σ = τ |
Кручение стержня прямоугольного сечения.
Для наглядности берем призматический стержень прямоугольного сечения из резины, на боковых поверхностях которого нанесена сетка.


При деформации замечаем:
1) Плоские сечения при деформации не остаются плоскими, а в круглом – остаются.
2) В углах стержня прямоугольники не искажаются → здесь касательное напряжение отсутствуют.
3) Наибольшее искажение получает прямоугольник сетки, расположенный в середине широкой стороны прямоугольника, здесь возникает максимальное касательное напряжение.
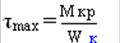 ,
,  ,
, 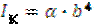 ,
,  – формулы для прямоугольного сечения.
– формулы для прямоугольного сечения.
 – зависят от соотношения сторон и приводятся в специальных таблицах.
– зависят от соотношения сторон и приводятся в специальных таблицах.
Потенциальная энергия при кручении.
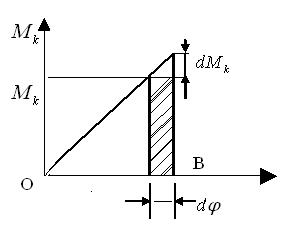
|
При закручивании стержня моментом  работа будет накапливаться в виде потенциальной энергии. работа будет накапливаться в виде потенциальной энергии.
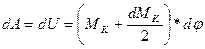 - элементарная работа.
Эта работа на чертеже изображается в виде площади заштрихованной фигуры. Нетрудно догадаться, что полная работа момента - элементарная работа.
Эта работа на чертеже изображается в виде площади заштрихованной фигуры. Нетрудно догадаться, что полная работа момента  на угловом перемещении на угловом перемещении 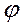 изображается площадью треугольника изображается площадью треугольника 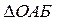 : : 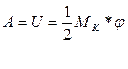
|
Потенциальная энергия при кручении:  или
или 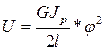
Дата добавления: 2016-02-13; просмотров: 5147;
