Резонанс в колебательном контуре при воздействии на него последовательности видеоимпульсов (накопительный резонанс).
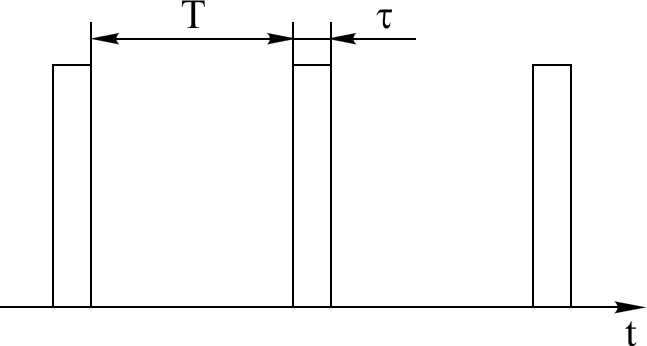
Параметры импульсной последовательности и контура. На колебательный контур с высокой добротностью Q>>1 (потери в контуре пренебрежимо малы) и большой постоянной времени τo воздействует последовательность прямоугольныхвидеоимпульсов (далее просто импульсов) с длительностью τ и периодом Т= 1/F=2p/Ω (рис. 4.32). Параметры контура: ωо=2πfo=2π /To; τo>>To.
| Рис. 4.32 Последовательность прямоугольныхвидеоимпульсов |
| Рис. 4.32 Последовательность прямоугольныхвидеоимпульсов |
| Рис. 4.32 Последовательность прямоугольныхвидеоимпульсов |
| Рис. 4.32 Последовательность прямоугольныхвидеоимпульсов |
Будем полагать длительность импульсов τ очень малой: τ<<Т; τ<<Тo. Поскольку длительность импульса намного меньше периода собственных колебаний контура, его воздействие воспринимается контуром как однократный электрический импульс (электрический "щелчок"). Этот электрический импульс заряжает конденсатор контура до некоторого значения напряжения, которое обозначим через U.
После окончания импульса конденсатор начинает разряжаться через индуктивность. В результате в контуре возникает свободное колебание u=Usinωot, продолжительность которого, благодаря большой добротности контура, во много раз превышает период следования импульсов Т. Поскольку контур имеет очень малые потери, то колебание, возникшее в нем под влиянием внешнего импульса, можно на достаточно большом интервале времени считать практически незатухающим. Амплитуда этого колебания U зависит от энергии внешнего импульса и параметров самого контура.
Через время Т на контур придет второй импульс и вызовет в нем второе свободное колебание u=Usin(ωot-j), аналогичное первому,но сдвинутое относительно него по фазе на угол j=ωoT=2πT/To.
После прихода второго импульса в контуре образуется суммарное колебание:
.
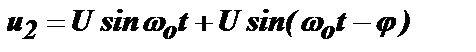Каждый следующий (n-ый) импульс, подобно двум первым, будет вызывать в контуре колебание u=Usin[ωot-(n-1)j], сдвинутое по фазе относительно первого на угол (n-1)j=(n-1)2πT/To.
После прихода в контур N-го импульса в контуре будет существовать сумма N колебаний одинаковой частоты, фазы которых образуют арифметическую прогрессию. Полагая, что за время поступления в контур N импульсов потери в контуре не приведут к заметному изменению амплитуды существующих в нем свободных колебаний, запишем выражение для суммарного колебания:
,
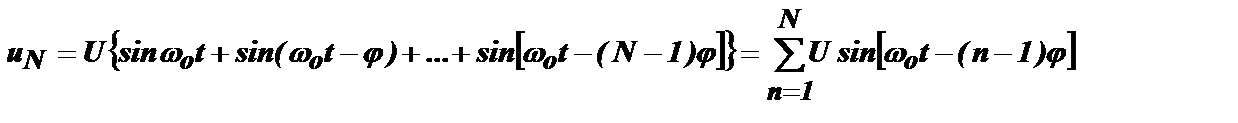Вид этого суммарного колебания зависит от фазового сдвига φ, т.е. от отношения T/To.
Процесс, который происходит в контуре, можно достаточно наглядно представить в виде векторных диаграмм. На рисунке 4.33 приведены примеры векторных диаграмм суммарных колебаний для нескольких значений N при двух значениях фазового сдвига: φ=+π/3 (рис. 4.33,а)и φ= –π/3 (рис. 4.33,б).
Из диаграмм видно, что суммарное колебание uN, вектор которого обозначен пунктиром, с ростом числа N изменяет свою амплитуду и становится похожим на колебание, модулированное по амплитуде. На рисунке 4.34 показано изменение этого колебания во времени. Кружками на рисунке отмечены моменты воздействия импульсов. Из-за разницы между Т и Т0 эти импульсы сначала как бы "подталкивают" контур, а затем "подтормаживают" его колебания. В результате и происходит изменение амплитуды суммарного колебания. Рассмотрим, как происходит это изменение.
Зависимость амплитуды суммарного колебания uN от угла j. Рассмотрим, как будет изменяться амплитудасуммарного колебания uN при изменении частоты fo, т.е. при изменении отношения Т/То. Это и будет зависимость uN от угла j= 2πT/To.
| Рис. 36 Векторная диаграмма сложения колебаний |
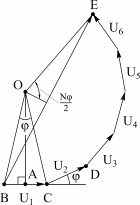Для этого мы должны вычислить сумму синусоид одной частоты, фазы которых образуют арифметическую прогрессию. Можно использовать различные способы, но наиболее наглядным будет геометрическое построение, при котором колебания изображаются в виде векторов с одинаковыми амплитудами U1=U2=U3=...=U, каждый из которых повернут на угол j, относительно предыдущего вектора. Тогда вся сумма может быть представлена в виде векторного многоугольника, показанного на рисунке 4.36. Поскольку амплитудасуммарного колебания uN на рисунке 4.36 соответствует вектору ВЕ, найдем зависимость длины этого вектора от угла j.
Концы векторов, составляющих векторный многоугольник, лежат на окружности с центром О. ∆ОВС=∆ОСД по признаку равенства трех сторон. Тогда ÐОВС=ÐОСD=ÐОCB. Поскольку сумма углов ÐОСB+ÐОCD дополняется углом j до 180о, то и угол при вершине треугольника ОВС, дополняющий ÐОВС и ÐОCB до 180о, также равен j. Отсюда угол ÐВОЕ=Nj.
Из треугольника ОВС следует: АВ=U/2=ОВ×sinj/2. Тогда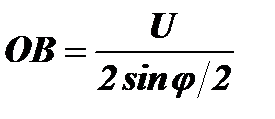 
. В свою очередь 
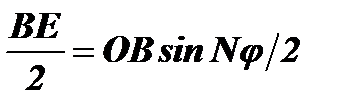. Отсюда ВЕ=2×ОВ×sinNj/2. Подставляя в это равенство величину ОВ, получим зависимость суммарного вектора ВЕ от j:
.
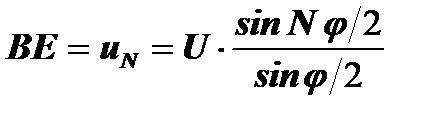Из рис. 4.33,в видно, что максимального значения амплитуда uN достигнет при j=0, так как в этом случае длина суммарного вектора будет равна сумме длин всех векторов. Однако в этом случае как числитель, так и знаменатель полученной дроби обращаются в нуль. Раскрыв неопределенность по правилу Лопиталя, получим максимальное значениеамплитуды uNмакс:
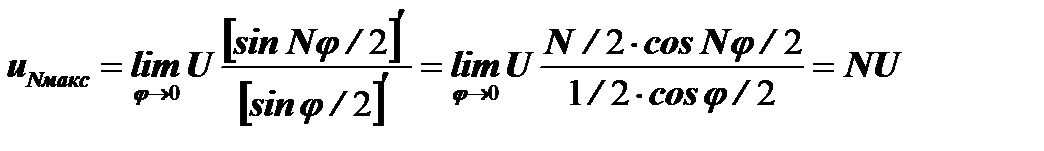Амплитуда uN обычно нормируется к своему максимуму и записывается в виде:
.
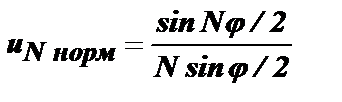На рисунке 4.37 показаны графики изменения числителя и знаменателя выражения для амплитуды uN при N=6 а также графики изменения самой амплитуды uN и ее квадрата, который называется интенсивностью, в зависимости от величины Nφ/2.
Функция uN − периодическая. Своих максимальных значений она достигает при j=2πn, где n=0,1,2,3.... Между этими максимумами функция uN имеет еще ряд нулей и побочных максимумов. Нули соответствуют нулям числителя величины uN (см. рис. 4.37), т.е. соответствуют значениям jo=2πn/N, а вторичные максимумы находятся между нулями и соответствуют значениям jмакс=±(2n+1)π/N.
Величина uN при N → ∞. На рисунке 4.37 показана зависимость суммарной амплитуды uN от j только для шести импульсов (N=6). Но с течением времени в контур будет поступать все больше импульсов. При этом главные максимумы функции uN будут расти, а их ширина будет уменьшаться. Вторичные же максимумы будут, наоборот, уменьшаться, а их число будет увеличиваться. Они все плотнее будут заполнять промежуток между главными максимумами. При N→¥ функция uN примет вид, показанный на рисунке 4.38.
Эта функция представляет собой резонансную характеристику идеализированного контура, не имеющего потерь, при воздействии на него бесконечной последовательности периодических видеоимпульсов. Из рисунка видно, что число резонансов в контуре в этом случае может быть бесконечно большим.
Рассмотрим, формирование резонансов в контуре.
Первый резонанс. Будем изменять частоту контура fo, наблюдая за сигналом на его выходе. Наибольший интерес представляет случай, когда в процессе перестройки контура его частота fo становится равной частоте повторения импульсов F. Тогда Т=Тo и в результате угол j= 2πТ/То=2π. Векторная диаграмма принимает вид, показанный на рисунке 4.33,в. На рис. 4.35 показано как складываются колебания, возникшие в контуре под воздействием двух первых импульсов. С ростом числа импульсов, поступающих в контур, амплитуда суммарного колебания монотонно и неограниченно растет. Это и есть резонанс, в результате которого на частоте fo появляется интенсивный отклик контура. Поскольку резонанс образуется благодаря накоплению в контуре колебаний, вызванных отдельными импульсами, его называют накопительным.
Второй, третий и последующие резонансы. Если установить частоту контура fo больше частоты следования импульсов F, то свободные колебания, возникшие в контуре под воздействием первого импульса, к моменту прихода второго импульса совершат один полный период и некоторую часть второго периода. Вектора на диаграммах рисунков 4.33,а и 4.33,б, совершив полный оборот, "пойдут" на второй круг, а суммарный вектор начнет принимать такие же положения, но уже во втором периоде. При j=+π/3 или j=–π/3 между соседними векторамифазовые сдвиги суммарных векторов на этих диаграммах станут равны j=2π+π/3 и φ=2π-π/3.
В результате второй импульс "подтолкнет" контур в той же фазе колебаний, но "пропустив" целый период. Теперь импульсы будут воздействовать на колебательный контур не в каждом периоде его колебаний, как это показано на рисунке 4.35, а через период. Но, так же, как и раньше, после каждого импульса в контуре остается свободное колебание с частотой fo, которое будет складываться с колебаниями, возбужденными предшествующими импульсами.
Когда Т станет равным 2Тo (fo =2F), свободные колебания в контуре снова начнут складываться в фазе и в контуре возникнет второй резонанс (рис. 4.39).
При дальнейшем увеличении частоты контура f0 до частоты fo=3F наступает третий резонанс. Внешние импульсы теперь "подталкивают" контур один раз за три периода его колебаний. В идеализированном контуре без потерь это обстоятельство никак не отразится на виде резонансной характеристики, так как при N→¥ число суммируемых свободных колебаний и, соответственно, их суммарная амплитуда стремятся к бесконечности.
Резонансы в контуре с потерями. Потери в контуре приведут к ограничению роста амплитуды суммарного колебания при резонансе. Эта амплитуда станет стационарной, когда энергия, поступающая в контур от каждого следующего импульса, будет равна потерям энергии в контуре за период следования импульсов. Очевидно, что с повышением номера резонанса амплитуда суммарного колебания в контуре будет становиться все меньше, поскольку энергия от источника импульсов поступает в контур через 2, 3 и более периодов собственных колебаний контура. Резонансная кривая контура для этого случая
примет вид, показанный на рисунке 4.40.
Более подробно резонанс в контуре с потерями будет рассмотрен в главе "Спектры".
Дата добавления: 2016-04-19; просмотров: 1610;