Акустический резонанс

Мы знаем, что резонансные явления – нарастание ампли­туды вынужденных колебаний системы – наступают тогда, когда частота вынуждающей силы совпадает с собственной частотой системы.

Все, кто когда-нибудь настраивал гитару, знает, что если две струны настроить «в унисон», т.е. на одинаковые частоты, то, возбудив колебания в одной струне, мы заставим звучать и другую, к которой вообще не прикасались.

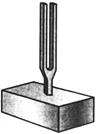Рис. 6.30

Другой пример акустического резонанса – камертон – это прибор для настройки музыкальных инструментов (рис. 6.30). Если по камертону ударить молоточком, он даст музыкальный звук строго определенной частоты. Но если поставить камертон на резонаторный ящик, открытый с одного конца, то громкость звучания резко увеличится… правда, только в том случае, если резонаторный ящик имеет «правильные» размеры. Колебания камертона вызывают вынужденные колебания воздуха в резонаторном ящике.

Читатель: Наверное, в ящике должна возникнуть стоячая волна, как на рис. 6.27,а. И если длина ящика равна l/4, то возникнет акустический резонанс.

Автор: Вы совершенно правы.

СТОП! Решите самостоятельно: А24, А28, В26, В28, В30–В32.

Заметим, что резонанс возникает в случае совпадения частоты внешнего колебания с любой из собственных частот воздушного столба. Поэтому резонансный ящик можно было бы взять длиной l/4, 3l/4 или 5l/4 (см. рис. 6.27,б, в).

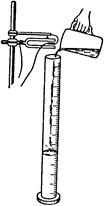Рис. 6.31

В подтверждении нашего утверждения рассмотрим следующий опыт. Возьмем высокий цилиндрический сосуд (высоты около 50 см) и заставим зву­чать над его отверстием камертон (рис. 6.31). Для опыта следует взять камертон с достаточно высокой частотой чтобы длина волны в воздухе была не слишком велика, например

n = 1000 Гц (l = 34 см).

Наливая в сосуд воду, мы услышим, что звук камертона при определенных уровнях воды значительно усиливается. Это как раз те уровни, при которых длина остающегося в сосуде воздушного столба равна нечетному числу четвертей длины волны (см. рис. 6.31). С частотой ка­мертона последовательно совпадают второй обертон воздушного столба (когда его длина составляет 5l/4), пер­вый обертон (при длине столба 3l/4) и основная частота (при длине стол­ба l/4).

Усиление звука при резонансе по­лучается потому, что сильные коле­бания воздуха на площади отверс­тия сосуда создают гораздо более сильную звуковую волну в окружаю­щем воздухе, чем колеблющиеся нож­ки самого камертона.

СТОП! Решите самостоятельно: А26, А27, В29, В33, В34, В35, С6.

Эффект Доплера[1]

Читатель: Я наблюдал такое явление: когда ко мне приближался поезд, машинист подавал звуковой сигнал – сирену. У меня сложилось такое впечатление, что когда поезд проехал мимо и стал удаляться, высота звука как-будто понизилась. Другими словами, пока поезд приближался, он как бы «пищал», в когда удалялся – «гудел». Я вот до сих пор не понимаю: это действительно так или мне просто показалось?

Автор: Это действительно так. Чтобы понять, почему это так, рассмотрим подробно, как распространяется звуковая волна от движущегося источника.

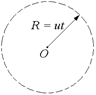Рис. 6.32

Назовем фронтом волны поверхность, до которой дошло возмущение от источника в данный момент времени. Например, фронтом волны от точечного источника будет сфера, в центре которой находится источник, при этом радиус сферы будет увеличиваться с такой скоростью, с которой распространяется волна в данной среде (рис. 6.32).

Пусть источник волн (звука) движется со скоростью υ < и, где и – скорость звука в данной фазе. Пусть в момент t = 0 источник звука находится в точке О. Точки О₁, О₂ и О₃ дают положения источника в моменты t, 2t, 3t. Каждая из этих точек может рассматриваться как центр сферической волны, испускаемой источником в тот момент, когда он находится в этой точке. Так как и > υ, то фронт каждой последующей волны целиком лежит внутри фронта предыдущей (рис. 6.33).

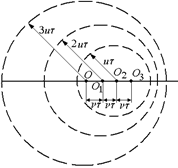Рис. 6.33

Пусть источник звука издает звук, частота которого равна n₀, если источник неподвижен. Выясним, с какой частотой будет восприниматься звук неподвижным приемником звука, если источник движется со скоростью υ < и (см. рис. 6.33)

Из рисунка видно, что длина испускаемых по разным направлениям волн различна и отличается от длины той волны, которую испускал бы неподвижный источник.

Если считать промежуток времени t равным периоду колебаний:

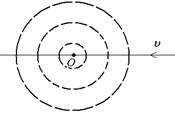Рис. 6.34

,

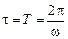то сферы на рис. 6.34 можно рассматривать как последовательные гребни волн, а расстояния между ними – как длину волны, излучаемой в соответствующем направлении. Видно, что длина волны, излучаемая по направлению движения источника, уменьшается, а в противоположном направлении увеличивается.

Пусть источник начинает очередной период излучения волны, находясь в точке О и, двигаясь в том же направлении, что и волна, заканчивает период, находясь в точке О₁. В результате длина излучения волны l¢ оказывается меньше длины волны l, излученной неподвижным источником на величину Т:

l – l¢ = υТ. (1)

Поскольку l = иТ, то из (1) получим

иТ – l¢ = υТ Þ l¢ = иТ – υТ = Т(и – υ).

Отсюда искомая частота равна

.

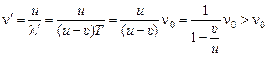Запомним:

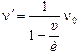. (6.19)

Автор: Как Вы считаете, звук какой частоты будут восприниматься приемником, если источник звука будет неподвижен, а приемник будет приближаться к нему со скоростью υ < u?

Читатель: Я думаю, что с частотой n¢, определенной формулой (6.19). Ведь если мы перейдем в систему отсчета, связанную с приемником, мы получим точно такую же ситуацию, как если бы источник приближался к неподвижному приемнику.

Автор: Не совсем так. Дело в том, что любой системе отсчета поверхности фронта волны в разные моменты времени в данном случае – это концентрические сферы (рис. 6.34), а в предыдущем случае – неконцентрические сферы. Поэтому ситуация уже другая. Длина волны источника l не изменится при движении приемника. Но изменится время, за которое приемник перемещается от одного гребня волны до другого, т.е. изменяется период колебаний. Для неподвижного приемника: Т = l/и, а для приемника, движущегося со скоростью υ, период равен

.

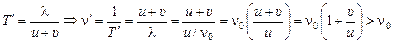Запомним формулу:

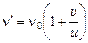. (6.20)

Эффект изменения частоты звука при движении источника или приемника звука называется эффектом Доплера.

СТОП! Решите самостоятельно: С9, С10.

Задача 6.5. Катер движется навстречу плоской волне длиной l = 6,0 м и частотой n = 1,0 Гц. С какой частотой n¢ волны ударяются о катер, если его скорость υ = 2,0 м/с?

Максимумы волн (гребни) отстоят друг от друга на расстояние, равное длине волны l. Значит, время, через которое гребни волны будут налетать на катер, равно

.

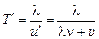Искомая частота

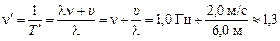Гц.

Ответ: 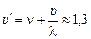Гц.

СТОП! Решите самостоятельно: В36, С8.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ[2]