Отражение и поглощение звука

По мере удаления от источника звука интенсивность звука убывает: чем дальше мы находимся от собеседника, тем хуже его слышно. Но если звуковая волна попадает на какое-либо препятствие, например стену или опушку леса, она частично поглощается, а частично – отражается. Очень хорошо отражается звук от гранитной скалы и очень плохо – от стены, обитой ватой, или от занавеса в театре. Поэтому в горах хорошо слышно эхо – отраженный звук, а в театре эха, как правило, не бывает.

Читатель: Если звуки отражаются от стен, почему мы так редко слышим эхо?

Автор: Дело в том, что, во-первых, в городе на улицах все-таки очень шумно, а во-вторых, человеческое ухо различает одинаковые звуки, если они приходят с интервалом не менее 0,1 с. А поскольку скорость звука достаточно высока (около 340 м/с), то для того, чтобы услышать эхо, надо находиться в очень тихом месте на достаточно большом расстоянии от отражающей поверхности.

СТОП! Решите самостоятельно: А12–А15, В14–В16, В18–В19.

Задача 6.3. На расстоянии s = 1068 м от наблюдателя ударяют молотком по железнодорожному рельсу. Наблюдатель, приложив ухо к рельсу, услышал звук на время Dt = 2,93 с раньше, чем он дошел до него по воздуху. Найти скорость звука и в стали. Скорость звука в воздухе υ = 340 м/с.

ut₂ = s, (2)

t₁ – t₂ = Dt. (3)

Выразим t₁ из (1) и t₂ из (2) и подставим в (3):

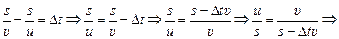
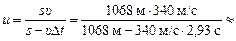5,10×10³ м/с.

Ответ: 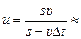5,10×10³ м/с.

СТОП! Решите самостоятельно: А16–А18, В20–В21, С3.

Дифракция звука

Мы знаем, что если на пути пучка света поставить непрозрачную поверхность, образуется тень: свет сколько-нибудь заметно не огибает препятствие.

Звук, наоборот, огибает препятствия (например, мы слышим звуки, доносящиеся из-за угла дома).

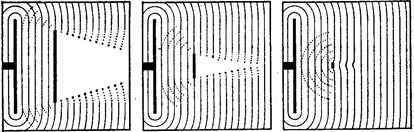
Поставим на пути прямолинейной поверхностной вол­ны в водяной ванне препятствия различного размера (рис. 6.13).

а б в

Рис. 6.13

Мы видим, что, когда препятствие доста­точно велико по сравнению с длиной волны l(рис. 6.13,а),тень от него сравнительно резкая: лишь у самых краев тени заметно небольшое волнение, указывающее, что волна слегка огибает край препятствия. По мере уменьшения препятствия тень оказывается менее ясно выраженной (рис. 6.13,б),а когда размеры препятствия становятся срав­нимыми с длиной волны, образования тени практически уже не происходит. Рис. 6.13,в показывает, что в этом слу­чае водяная волна огибает препятствие, и позади него она распространяется почти так же, как если бы препят­ствия не было. Это огибание волной края препятствия, особенно отчетливо наблюдаемое при малых по сравнению с длиной волны размерах препятствия, называется дифрак­цией.

Обратим внимание на следующее обстоятельство. Длина звуковой волны в воздухе при частоте 1000 Гц равна 33,7 см, а при частоте 100 Гц она составляет уже 3,37 м. Таким об­разом, размеры обычно окружающих нас предметов (за исключением больших домов) отнюдь не велики по сравнению с длиной звуковой волны.

Отсутствие в обычных условиях хорошо выраженной звуковой тени и есть результат дифракции звуковых волн, которую мы наблюдаем, таким образом, буквально на каждом шагу. Дифракцию световых волн наблюдать не так просто, как в случае звука, так как длины световых волн очень малы – всего несколько десятитысячных долей мил­лиметра.

СТОП! Решите самостоятельно: В22, В23.

Наложение волн

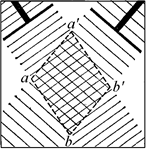Рис. 6.14

Проделаем следующий опыт с волнами в водяной ванне. Заставим колебаться на двухупругих пластинках две линейки, ударяющие по поверх­ности воды и создающие две плоские волны (рис. 6.14). Линейки поставлены под углом друг к другу так, что посылае­мые ими волновые пучки пересе­каются в области aa'b'b и затем вновь расходятся. Опыт показы­вает, что прохождение каждой из волн через область aa'b'b со­вершенно не зависит от присут­ствия или отсутствия другой вол­ны, т.е. волны, исходящие от двух колеблющихся линеек, проходят друг через друга без влияния на распространение каждой из них. Никакого влияния одной вол­ны на распространение другой не происходит.

То же самое откосится и к звуковым волнам: распростране­ние звука от любого источника не испытывает никакого влияния со стороны других звуковых волн, как угодно распространяющихся в это время через те же об­ласти среды.

Что же происходит в тех областях пространства, в ко­торых подобно участку поверхности aa'b'b на рис. 6.14волны налагаются одна на другую?

Каждая частица среды, находящаяся на пути волны, совершает колебания с периодом этой волны. Если эта ча­стица находится на пути двух волн, то она одновременно участвует в колебаниях обеих волн, т. е. ее движение представляет собой сумму этих колебаний. Таким образом, наложение двух (или большего числа) волн есть сложение их колебаний в каждой точке среды, через которую обе эти волны (или все эти волны) проходят. Как мы видели, наложение волн в каком-либо месте не влияет на их распространение как через это место, так и вне его.

Интерференция волн

Однако если происходит нало­жение волн одинаковой частоты, имеющих, следовательно, одинаковую длину волны, то могут возникнуть своеобразные и очень важные явления, к которым мы теперь и перейдем.

Укрепим на одной колеблющейся пластинке два про­волочных острия, которые будут одновременно ударять по поверхности воды в нашей ванне. Мы получим две коль­цевые волны с одинаковой длиной волны, разбегающиеся из двух центров и налагающиеся друг на друга.

Если расстояние между остриями больше длины вол­ны, то мы увидим картину, изображенную на рис. 6.15. Про­исходит не просто усиление волнения воды, чего можнобыло бы ожидать на первый взгляд, а более сложное явле­ние. На поверхности воды получается ряд областей, в ко­торых колебания особенно сильны (максимумы аа', bb', ...), разделенных областями сильно ослабленного волнения (минимумы mm', пп', ...). Такая картина чередующихся максимумов и минимумов колебания называется интер­ференционной картиной, а само явление наложения волн, когда оно приводит к образованию этой картины, – интерференцией волн.

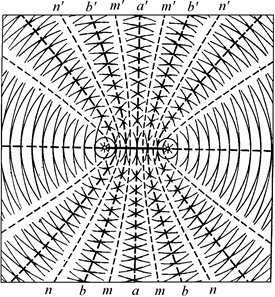Рис. 6.15

Происхождение интерференционной картины в данном опыте позволит нам понять, в чем заключаются условия возникновения интерференции вообще.

В каждой точке колебание поверхности воды является суммой колебаний, вызванных каждой волной в отдельно­сти. Пусть в каком-то месте в данный момент сошлись гребни обеих волн, т. е. обе волны пришли сюда в одина­ковой фазе. В этой точке получится усиленный подъ­ем воды. Через полпериода (Т/2) гребни сменятся впадина­ми, причем у обеих волн одновременно, так как их период одинаков. Поверхность воды сильно опустится. Таким образом, в указанном месте будет происходить усиленное колебание. Наоборот, в та­ком месте, где сходятся гребень одной волны с впадиной другой, т. е. где волны проходят в противополож­ных фазах, колебания взаимно ослабятся. Ослабле­ние будет происходить все время, ибо в любой момент фазы обеих волн будут противоположны и, в частности, через полпериода в этой точке будет впадина первой волны и гребень второй. Таким образом, существенным для воз­никновения интерференционной картины является то обстоятельство, что волны, идущие из обоих центров, согласованы между собой: сдвиг фаз между коле­баниями обеих волн в каждой данной точке остается все время постоянным.

Если бы мы произвольным образом меняли фазу колеба­ний одного из источников, тогда и в каждой точке поверхности воды фазы обоих колебаний то совпадали бы, то расходились, и расположение максимумов и минимумов не было бы устойчивым. Точно так же, если бы периоды колебаний обеих волн были различны, то во всякой точке поверхности усиление колебаний сменялось бы их ослабле­нием, потом опять усилением и т. д. Чем больше разница периодов или чем быстрее меняется фаза одного из колебаний, тем быстрее меняется расположение максимумов и минимумов.

Говоря об интерференционной картине, имеют в виду устойчивую, не изменяющуюся со временем картину чередо­вания максимумов и минимумов. Подобная устойчивая картина возникает лишь в том случае, когда налагающиеся волны имеют одинаковый период и неизменный сдвиг фаз колебаний в каждой точке. Такие волны называются коге­рентными.

Следовательно, устойчивая интерференция может иметь место только при условии когерентности волн.

В рассмотренном нами случае когерентность обеспечи­вается тем, что оба источника (проволочные острия) связаны друг с другом, будучи прикреплены к одной и той же колеблющейся пластинке.

В этом случае оба когерентных источника дают волны, выходящие из места их возбуждения в одной фазе, т. е. греб­ни (или впадины) выходят из обоих источников одно­временно. Можно было бы представить себе устрой­ство, при котором одна из волн запаздывает по фазе относительно другой. Но если это запаздывание со­храняется в течение опыта неизменным, то источ­ники также являются когерентными (хотя и не совпадаю­щими по фазе) и порождаемые ими волны дают устойчивую интерференционную картину. Таким образом, для когерент­ности необходим неизменный сдвиг фаз обеих волн; абсолютное значение же этого сдвига не играет роли.