Условия образования максимумов и минимумов

Мож­но ли сказать заранее, где в интерференционной картине получатся максимумы колебаний, а где минимумы?

Рассмотрим рис. 6.16, на котором изображена схема ин­терференции волн от двух когерентных источников S₁ и S₂.

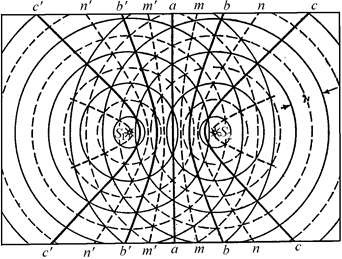
Рис. 6.16

Пусть оба источника колеблются в одной фазе, т. е. гребни (или впадины) выходят из них одновременно. Очевидно, на линии аа,каждая точка которой одинаково удалена и от S₁ и от S₂, получится максимум колеба­ний, так как гребни (или впадины) обеих волн будут дости­гать точек этой линии одновременно, и фазы обеих волн здесь совпадут. Точно так же усиление колебаний полу­чится на линии bb, все точки которой на одну длину волны lближе к S₂, чем к S₁. Во всех точках линии bb волна от источника S₁ будет запаздывать ровно на один период по сравнению с волной от источника S₂, а значит, фазы обеих волн опять совпадут. То же самое будет иметь место и на линии сс, точки которой на 2lближе к источнику S₂, чем к S₁,т. е. одна волна запаздывает на два периода по сравнению с другой, и на линиях b'b', с'с' и т. д., точки которых расположены на l, 2l и т. д. ближе к источнику S₁, чем к S₂.

Такое же рассуждение показывает, что на линиях mm, пп, ... и т'т', п¢п', ..., все точки которых расположены ближе к одному из источников, чем к другому, на полвол­ны (l/2), три полуволны (3l/2) и вообще нечетное число полу­волн, получится ослабление колебаний — минимум. Дей­ствительно, во всех точках этих линий гребень одной вол­ны будет встречаться с впадиной другой, или, иначе гово­ря, фазы обеих волн будут противоположны.

Будем называть разность расстояний от какой-либо точки до источников S₁и S₂ разностью хода двух интерфе­рирующих волн до этой точки. Тогда найденное правило можно коротко формулировать следующим образом.

Максимумы интерференционной картины от двух колеблющихся в одинаковой фазе источников получаются в тех местах, где разность хода равна целому числу длин волн, или, что то же, четному числу полуволн, а минимумы – в тех местах, где разность хода равна нечетному числу полуволн.

Задача 6.4. Два когерентных источника звука колеблются в одинаковых фазах. В точке, отстоящей от первого источника на 2,00 м, а от второго на 2,50 м, звук не слышен. Определить частоту колебаний источников. Скорость звука 340 м/с.

и = 340 м/с l1 = 2,00 м l2 = 2,50 м	Решение. Поскольку в указанной точке достигается минимум амплитуды, то разность хода двух звуковых волн равна нечетному числу полуволн: 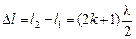, (1) где k = 0, 1, 2, …
n = ?

Согласно формуле (6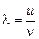.2)

. (2)

Подставив (2) в (1), получим

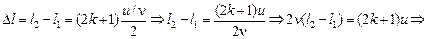
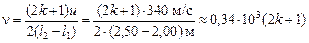Гц.

Ответ: 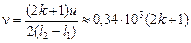Гц, где k = 0, 1, 2…

СТОП! Решите самостоятельно: А19–А21, В24, В25, С4, С5.

Стоячие волны

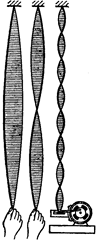Рис. 6.17 Рис 6.18

На пути волны, создаваемой ударяющей по воде линей­кой, мы ставим пластинку, параллельную линейке, т. е. перпендикулярную к направлению распространения волны (рис. 6.17). Опыт показывает, что когда волна, бе­гущая от линейки, отражается и идет обратно, между ко­леблющейся линейкой и отражающей пластинкой полу­чается ряд параллельных им и не перемещающихся полос, удаленных друг от друга на пол­волны. Как и всегда при интерференции, эти полосы представляют собой чередование максимумов и минимумов, причем в минимумах поверхность во­ды практически неподвижна.

Стоячую волну можно получить и в упругом шнуре, один конец которого закреплен. Если привести в колебательное движение свободный конец шнура, мы увидим, что волна, бегущая от свободного конца шнура, отражается от закрепленной точки и бежит навстречу волне, создаваемой колебаниями свободного конца шнура (рис. 6.18).

На шнуре образуются чередующиеся неподвижные точки и точки, в которых размах колебаний наибольший. Неподвижные точки называются узлами стоячей волны, а места наибольшей амплитуды колебаний – ее пучностями. Расстояние между двумя соседними узлами (или двумя соседними пучностями) равно половине длины волны. Чем быстрее мы колеблем нижний конец шнура, т. е. чем выше частота, тем короче длина волны и тем боль­ше узлов и пучностей укладывается на шнуре.

Читатель: Честно говоря, не очень понятно, почему сложение падающей и отраженной волн дает именно такую картину…

Автор: Давайте разберемся в этом чисто теоретически: получим уравнение стоячей волны.

Прежде всего, заметим один важный экспериментальный факт: при отражении волны знак смещения меняется на противоположный, т.е. если мы пустили по шнуру волну «горбом» вверх (рис. 6.19,а), то отразится она «горбом» вниз (рис. 6.19,б).

Рис. 6.19

С чисто математической точки зрения это означает, что фаза волны при отражении увеличивается на p .

Читатель: А есть ли этому экспериментальному факту какое-либо теоретическое объяснение?

Автор: Объяснить это можно так: в момент отражения волнового импульса на закрепленный участок шнура действует перпендикулярная к шнуру сила со стороны стенки. Действие этой силы не только удерживает ко­нец шнура в покое, но и порождает отраженную волну со сме­щением участков шнура в противоположном направлении, как будто по шнуру ударили сверху вниз (см. рис. 6.19,б).

Изменение фазы волны можно объяснить и по-другому. При отражении волны от закрепленного конца амплитуда ко­лебаний конца равна нулю. Это может быть лишь в том слу­чае, если колебания шнура, вызванные прямой и обратной волной на конце шнура, происходят в противофазе.

Получим уравнение стоячей волны на резиновом шнуре длиной l. Уравнение бегущей волны в направлении оси X, сов­падающем с растянутым шнуром, имеет вид:

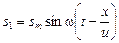. (6.14)

Волна проходит от начала шнура (точка х₀= 0) до конца (x_l = l) иобратно до точки на расстоянии х от начала шнура путь l + (l – x) = = 2l – x (рис. 6.20).

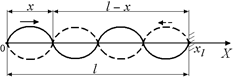Рис. 6.20

Смещения в отраженной волне вследствие измене­ния фазы при отражении имеют противоположный знак по сравнению со смещением s₁ в бегущей волне. Если пренебречь затуханием, то уравнение отраженной волны запишется сле­дующим образом:

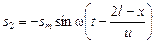. (6.15)

Результирующее смещение произвольной точки шнура с координатой х равно

.

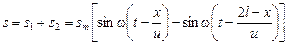Воспользуемся известной тригонометрической формулой

,

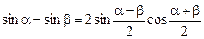тогда, полагая 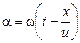, , 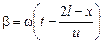получим

.

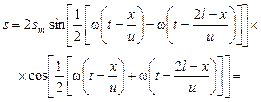
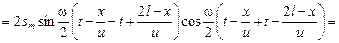
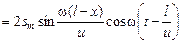Итак, уравнение стоячей волны имеет вид

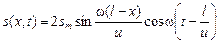. (6.16)

Из уравнения (6.16) видно, что каждая точка стоячей волны совершает гармонические колебания с той же циклической частотой w, которую имеют падающая и отраженная волны. При этом амплитуда этих колебаний зависит от координаты х:

Амплитуда = .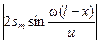

Ясно, что в тех точках, в которых синус равен нулю, колебания не совершаются, это – узлы волны. Найдем их координаты:

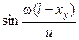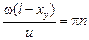= 0 Þ Þ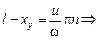

,

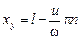где п = 0, 1, 2… Или, учитывая, что 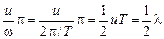, можем записать

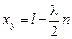. (6.17)

Это – координаты узлов стоячей волны.

Точки, в которых амплитуда максимальна, то есть синус равен 1 или –1, образуются пучности стоячей волны. Найдем их координаты:

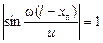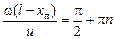Þ Þ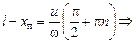

.

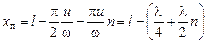Итак, пучности стоячей волны имеют координаты

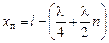, (6.18)

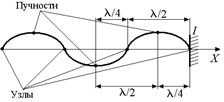Рис. 6.21

где п = 0, 1, 2…

Как видно из формул (6.17) и (6.18), узлы и пучности отстоят друг другу на l/4, а расстояние между двумя соседними узлами, как и между двумя соседними пучностями, равно l/2 (рис. 6.21).

Множитель 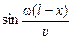в формуле (6.16) при переходе через нулевое значение меняет знак, вследствие чего фазы колебаний по разные стороны от узла отличаются на p. Это означает, что точки, лежащие по разные стороны от узла, колеблются в противофазе, а все точки, находящиеся между двумя узлами, колеблются синфазно, т.е. в одной фазе, но с разными амплитудами. На рис. 6.22 показаны положения точек стоячей волны в моменты времени t и t + Dt.

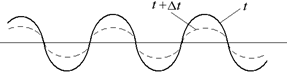Рис. 6.22

СТОП! Решите самостоятельно: А22, А25.