Свободные колебания струны
Для опытов со струной удобен прибор, изображенный на рис. 6.23. Один конец струны закреплен, а другой перекинут через блок, и к нему можно подвешивать тот или иной груз. Таким образом, сила натяжения струны нам известна: она равна весу груза. Доска, над которой натянута струна, снабжена шкалой. Это позволяет быстро определить длину всей струны или какой-либо ее части.
 Рис. 6.23
Рис. 6.23
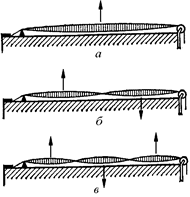 Рис. 6.24
Рис. 6.24
|
Оттянув струну посередине и отпустив, мы возбудим в ней колебание, изображенное на рис. 6.24,а. На концах струны получаются узлы, посередине – пучность.
С помощью этого прибора, меняя массу груза, натягивающего струну, и длину струны (перемещая добавочный зажим со стороны закрепленного конца), нетрудно экспериментально установить, чем определяется собственная частота колебания струны.
Автор: Как Вы думаете, как будет изменяться частота колебания струны, если мы будем увеличивать: а) силу натяжения; б) плотность материала; в) диаметр струны; г) длину струны?
Читатель: Я знаю из опыта игры на гитаре, что чем сильнее натянута струна, тем выше она звучит, т. е. F Þ n. Если же мы будем увеличивать плотность, диаметр или длину струны, то тем самым мы увеличим ее массу, т. е. струна будет более инертной, значит, период ее колебаний увеличится, а частота, соответственно, уменьшится.
Автор: Вы правы. Добавлю только, что в струнных инструментах сила натяжения F создается, конечно, не подвешиванием грузов, а растягиванием струны при накручивании одного из ее концов на вращающийся стерженек (колок). Поворотом колка, т. е. изменением силы натяжения F, осуществляется и настройка струны на требуемую частоту.
Поступим теперь следующим образом. Оттянем одну половинку струны вверх, а другую – вниз с таким расчетом, чтобы средняя точка струны не сместилась. Отпустив одновременно обе оттянутые точки струны (отстоящие от концов струны на четверть ее длины), мы увидим, что в струне возбудится колебание, имеющее, кроме двух узлов на концах, еще узел посередине (рис. 6.24,б)и, следовательно, две пучности. При таком свободном колебании звук струны получается в два раза выше (на октаву выше, как принято говорить в акустике), чем при предыдущем колебании с одной пучностью, т. е. частота равна теперь 2n. Струна как бы разделилась на две более короткие струны, натяжение которых прежнее.
Можно возбудить далее колебание с двумя узлами, делящими струну на три равные части, т. е. колебание с тремя пучностями (рис. 6.24, в). Для этого нужно оттянуть струну в трех точках, как показано стрелками на рисунке. Частота этого колебания равна 3n. Оттягивая струну в нескольких точках, трудно получить колебания с еще большим числом узлов и пучностей, но такие колебания возможны. Их удается возбудить, например, проводя по струне смычком в том месте, где должна получиться пучность, и слегка придерживая пальцами ближайшие узловые точки. Такие свободные колебания с четырьмя, пятью пучностями и т. д. имеют частоты 4n, 5n и т. д.
Итак, у струны имеется целый набор колебаний и соответственно целый набор собственных частот, кратных наиболее низкой частоте n. Частота n называется основной, колебание с частотой n называется основным тоном, а колебания с частотами 2n, 3n и т. д. – обертонами (соответственно первым, вторым и т. д.).
В струнных музыкальных инструментах колебания струн возбуждаются либо щипком или рывком пластинкой (гитара, мандолина), либо ударом молоточка (рояль), либо смычком (скрипка, виолончель).
Читатель: Получается, что гитарная струна может свободно колебаться и с частотой n, и с частотой 2n, и с частотой 3n и т.д. Так с какой же частотой она колеблется на самом деле?
Автор: Со всеми сразу! Колебания струны – это результат сложения колебаний с разными частотами (n, 2n, 3n, и т.д.) и разными амплитудами, которые происходят одновременно. Поэтому если мы попытаемся найти зависимость смещения какой-либо точки 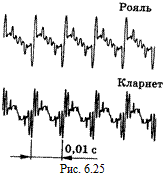 струны от времени, то получится отнюдь не синусоида, а гораздо более сложная кривая, которая и определяет тембр звука данного инструмента. В качестве примера на рис. 6.25 приведен график зависимости смещений от времени s(t) рояля и кларнета.
струны от времени, то получится отнюдь не синусоида, а гораздо более сложная кривая, которая и определяет тембр звука данного инструмента. В качестве примера на рис. 6.25 приведен график зависимости смещений от времени s(t) рояля и кларнета.
СТОП! Решите самостоятельно: А23, В27.
Дата добавления: 2016-04-11; просмотров: 1915;
