Вращающийся Aвектор, равный сумме векторов A1 иA2 , изображающих соответственногармонические колебания1 - го грузикаотносительно 2- го грузикаи гармонические колебания 1 страница

2грузикавместе с 1 грузикомотносительно O началакоординатв произвольный момент

t времени, т.е. A = A₁ + A₂, изображает результирующее колебание1 грузика относительно O начала координат.

Фазы колебаний1 - го (2.14) и2- го (2.15) грузиков на рис.2.5 в данный момент t времени обозначены соответственно Ф₁ и Ф₂, а фаза Фрезультирующего колебания1 - го грузика относительно O начала координат обозначена Ф. В произвольный момент времени Ф₁ и Ф₂ фазы колебаний1 - го (2.14) и2- го (2.15) грузиков имеют следующий вид:

Ф₁ = ω₁ t+ φ₁; Ф₂ = ω₂ t+ φ₂. (2.16)

координат; z - результирующаякоордината 1 - го грузика, т.е. отклонение от положения равновесия 1 - го грузикав зависимости от t времени, когда учитываются его (2.11) z₁ колебания на а пружине в системе координат, связанной со 2 - ым грузиком,а также учитываются его (2.12) z₂ колебанияна bпружинекак единое целое со 2 - ым грузиком относительно O начала координат.

По теореме косинусов A модуль результирующеговектораA (рис. 02.0.5)навекторной диаграмме имеет следующий вид:

A = {A₁² + A₂² - 2A₁A₂ cos [π -(Ф₂ -Ф₁)]} ^1/2 =[A₁² + A₂² + 2A₁A₂ cos (Ф₂ -Ф₁)] ^1/2.(2.18)

В выражении (2.18) Ф₂ - Ф₁ является разностью Ф₂ фазыгармонических колебаний2- гогрузикавместе с 1 - ымгрузикомотносительно O началакоординатв произвольный момент

t времени и Ф₁ фазыгармонических колебаний1 - го грузикаотносительно 2- го грузика.

Фаза Ф результирующеговектораA (рис.2.5)навекторной диаграмме результирующего поOZ осиколебания1 - го грузикаотносительно O началакоординат в (2.14) выраженииимеет следующий вид: tgФ = (A₁ sinФ₁+ A₂ sinФ₂)/(A₁cosФ₁+ A₂cosФ₂) ↔ ↔ Ф = arctg[(A₁ sinФ₁+ A₂ sinФ₂)/(A₁cosФ₁+ A₂cosФ₂)].(2.19) Два z₁ и z₂ гармонических колебания называются когерентными, если Ф₂ - Ф₁ разностьих фазне зависит от t времени и имеет следующий вид: Ф₂ - Ф₁ = (ω₂ - ω₁)t + (φ₂ - φ₁) = const (2.20) Выполнение условия (2.20) возможно, если ω₂ = ω₁ = ω. Тогда Ф₂ - Ф₁ разностьфаз когерентныхколебаний равна следующей φ₂ - φ₁ разности их начальных фаз: Ф₂ - Ф₁ = φ₂ - φ₁ = φ₀ .(2.21) При выполнении (2.21) условия результирующее(2.17)z колебание двух складываемых

z₁ и z₂ гармоническихколебаний одного направления является тоже гармоническим с той же циклическойω частотой, что и эти складываемые колебания, вследствие чего zрезультирующееколебание двух складываемых z₁ и z₂ гармоническихколебаний имеет следующий вид: z = z₁ + z₂ = Acos(ωt + φ₀). (2.22) Выражение для A амплитуды результирующегоколебания как суммыдвух когерентныхколебаний получается подстановкой (2.21) Ф₂ - Ф₁ = φ₂ - φ₁ разностифаз когерентныхколебаний в (2.18), вследствие чего получается следующее выражение: A = [A₁² + A₂² + 2A₁A₂ cos(φ₂ - φ₁)]^1/2, (2.23)

Выражение(2.19) начальной Ф₀фазы результирующегоколебания как суммыдвух когерентныхколебаний получается подстановкой в (2.13)начальногоt₀ времени, равного нулю, т.е. t₀ = 0, вследствие чего получается следующее выражение для начальной Ф₀фазы результирующегоколебания: Ф₁₀ = φ₁; Ф₂₀ = φ₂ ↔ tgФ₀ = (A₁ sinφ₁+ A₂ sin φ₂)/(A₁cos φ₁ + A₂cos φ₂) ↔ ↔ Ф₀ = arctg[(A₁sinφ₁+ A₂ sinφ₂)/(A₁cosφ₁+ A₂cosφ₂)], (2.24)где (2.14) A₁ , φ₁, рад - соответственно амплитудаиначальная фазаприколебаниях 1 - го грузика на aпружинеотносительно 2- го грузика; (2.15) A₂ , φ₂, рад - соответственно амплитуда иначальная фазаприколебаниях 1 - го грузика на bпружинекак единое целое со 2 - ым грузиком относительно O начала координат.

В зависимости от значения φ₂ - φ_{1 =} φ₀разности начальных фаз складываемых колебаний

A амплитуда результирующего колебания согласно выражению (2.23) изменяется в следующих пределах: от A = | A₁- A₂| при φ ₂ - φ ₁ = ±(2m + 1)π (2.25) до A = A₁+ A₂при φ ₂ - φ ₁ = ±2mπ, (2.26) где m = 0,1,2,… - любое целое неотрицательное число.

Если (2.26) φ₂ - φ₁ = φ₀ = ±2mπ, т.е.разность начальных фаз складываемых когерентных колебаний кратна 2π , то говорят, что складываемые колебания физической величины синфазны.В случае сложения синфазных механических,электромагнитныхили электромеханическихколебаний A амплитуда результирующего колебанияскладываемыхфизических величин максимальна.

Если (2.25) φ₂ - φ₁ = φ₀ = ±(2m + 1)π,т.е.разность начальных фаз складываемых когерентных колебаний кратна нечётномучислу π , то говорят, что складываемые колебания физической величины противофазны.В случае сложения противофазных механических,электромагнитныхили электромеханическихколебаний A амплитуда результирующего колебанияскладываемыхфизических величин минимальна.

Результирующие колебания двух складываемых (2.17) гармоническихколебаний одного направления,циклические(2.2)частотыω₁ и ω₂ колебаний которых различны, т.е.ω₂ ≠ ω₁, являются некогерентными колебаниями, т.к. разность их фаз Ф = Ф₂ - Ф₁ = (ω₂ - ω₁)t + (φ₂ - φ₁) непрерывно изменяется с течением t времени. При сложении таких колебаний получаются негармонические результирующие колебания. Негармонические колебания, получающиеся в результате сложения двух одинаково направленных гармонических колебанийсблизкимиω₁, ω₂ (2.14), (2.15) циклическими частотами,т.е.| ω₂ - ω₁| << ω₁, называются биениями.

Сложение взаимно перпендикулярных гармонических колебаний равных и кратных частот.

Пусть материальнаяM точка одновременно колеблется вдоль OY и OZ осей координатв соответствии со следующими уравнениями:

y = A₁cos(ωt + φ₁) ; z = A₂ cos(ωt + φ₂ ),(2.27) где y, z - координата материальнойM точки в зависимости от t времени при колебаниях соответственновдоль OY и OZ осей координат; ω- циклическаячастота(2.2) гармоническихколебанийматериальнойM точки, одинаковая по OY и OZ осям координат; A₁ , φ₁, рад - соответственно амплитудаиначальная фазаприколебанияхматериальнойM точки по OY оси;

A₂ , φ₂, рад - соответственно амплитудаиначальная фазаприколебанияхматериальнойM точки по OZ оси.

OYZ плоскости можно найти, выразив из (2.24) уравнения z = A₂ cos(ωt+ φ₂ ) колебания материальной M точки по OZ оси параметр ωt =[arcos(y/A₂)] - φ₂, подставив этот параметр ωt в уравнение y = A₁ cos(ωt+ φ₁) колебания материальной M точки по OY оси. Исключив таким образом из уравнений (2.27) tвремени, получаем следующее уравнениеТ траекториирезультирующего движения материальной M точки в OYZ плоскости: (y²/A₁²) + (z²/A₂²) - (2yz/ A₁A₂)cos(φ₂ - φ₁) = sin²(φ₂ - φ₁). (2.28)

На OYZ плоскости (2.28) уравнение Т траектории результирующего движения материальной M точки представляет собой эллипсс A₁ и A₂ полуосями, равными (2.27) A₁ и A₂ амплитудам складываемых взаимно перпендикулярных гармоническихколебаний этой материальнойM точки.

являющегося Т траекторией(рис. 02.0.6)результирующего движения материальной M точки в

OYZ плоскости, совпадают с OY и OZ осями координат, а размеры полуосей этого эллипса равны

A₁ и A₂ амплитудам складываемых(2.24)взаимно перпендикулярных гармоническихколебанийматериальнойM точки.

Уравнение Т траектории результирующего движения материальной M точки (2.28) в этом случае примет следующий вид: (y²/A₁²) + (z²/A₂²) = 1. (2.29) МатериальнаяM точка, колеблющаяся вдоль взаимно перпендикулярныхнаправлений с одинаковой циклической(2.2)ωчастотой, совершает один полный оборот по Т траектории,представляющийсобой(рис. 02.0.6) эллипс,за время, равное T = 2π/ω периоду складываемыхколебаний.

Если A₁ и A₂ амплитуды складываемых(2.27)взаимно перпендикулярных гармоническихколебанийматериальнойM точки равны друг другу, т.е. A₁ = A₂, то Т траектория(2.29)результирующего движения материальной M точки представляет собой окружность.

В тех случаях, когда φ₂ - φ₁ разность начальных фаз складываемыхколебаний кратна π, т.е. φ₂ - φ₁ = ±mπ, где m = 0, 1, 2,…, n, то Т траектория(2.28) результирующего движения материальной M точкииз эллипса вырождаетсяв отрезок прямой, вследствие чего уравнение Т траектории этого результирующего движения материальной M точки примет следующий вид: z = ± ( A₁/ A₂)y. (2.30) Знак "+" в выражении (2.30) соответствует сложению взаимно перпендикулярных гармоническихколебаний, когда эти колебания синфазны, а знак "-" соответствует сложению противофазных колебаний.

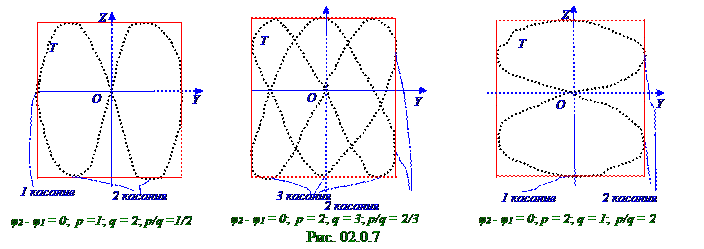
Сложение взаимно перпендикулярных гармонических колебаний с циклическими частотамиpω и qω, где p и q - целые числа: y= A₁ cos(pωt+ φ₁); z = A₂ cos(qω t+ φ₂), где p и q - целые числа, приводит к движению материальной M точкипо траектории, названной фигурой Лиссажу. На рис. 02.0.7 приведены различные случаи Т траекторийдвижения материальной M точки, колеблющейся во взаимно перпендикулярныхнаправлениях с указанными соотношениями циклических pω и qω частот.

Отношение частот pω и qω складываемых колебаний равно отношению числа касанийсоответствующей им фигуры Лиссажу со стороной прямоугольника, параллельнойOZоси, и со стороной, параллельнойOY оси.

Лекция 5. Динамика гармонических колебаний. Кинетическая и потенциальная энергия гармонического осциллятора. Полная механическая энергия и импульс гармонического осциллятора. Фазовая траектория колебательной системы. Дифференциальное уравнение гармонических колебаний физического маятника и его решение. Квазиупругая сила колебательной системы. Дифференциальное уравнение свободных затухающих колебаний и его решение. Декремент и логарифмический декремент свободных затухающих колебаний. Добротность колебательной системы. Дифференциальное уравнение вынужденных колебаний и его решение. Механический резонанс колебательных процессов

Динамика гармонических колебаний. Кинетическая и потенциальная энергия гармонического осциллятора и импульс гармонического осциллятора

У некоторых механических систем потенциальная W_p энергия является функцией одной переменной. Если у такой механической системы существует устойчивоеположение равновесия, в котором потенциальная W_p энергия этой механической системы имеет минимум, а полная W_Σ энергия, т.е. сумма кинетическойW_k и потенциальной W_p энергии, величина постоянная, т.е. не зависят от t времени, то такую механическую систему называют гармоническим осциллятором.

В гармоническим осцилляторе материальная точкаm массой совершает свободные незатухающие колебанияпод действием упругойили квазиупругойсилы.

маятника заменена равной этой Δy проекции величиной y координаты, отсчитанной от O началакоординат, которое находится в точке устойчивогоравновесия пружинного маятника.

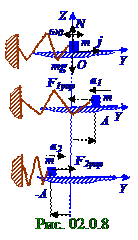
В (2.31) применено равенство m(d²y/dt²) = F_упрy потому, что по OY оси на материальную точкуm массой действует единственная сила, которой является (рис. 02.0.8) сила упругости пружины, вектор F_упр (1.104)из раздела 01.0 "Физические основы механики" которой является равнодействующим

j единичному вектору.

Если пружинный(рис. 02.0.8)маятник сжат, т.е. y₂ координата материальной точкиm массой меньше нуля, то векторы a₂ ускорения и F_2упрсилы упругости коллинеарны j единичному вектору(1.1) из раздела 01.0.0 "Физические основы механики" и направлены в одну сторону с этим

j единичным вектором.

По аналогии с (1.97) – (1.107) из раздела 01.0 "Физические основы механики" и с

учётом (2.31) определяем W_pпотенциальную энергиюматериальной точки m массой при её отклонении (2.28) на величину y = s(t) = A cos(ωt+ φ₀) относительно равновесия под воздействием упругой силыF_упрy в заданный моментtвременииз следующего выражения:

W_p y

dW_p = - F_упрydy ↔ dW_p = mω₀²ydy ↔ W_p = ∫dW_p = ∫mω₀ ²ydy = (mω₀ ²y²)/2 = 0 0

= (mω₀²A²/2)cos²(ω₀t+ φ₀) = (mω₀²A²/4)[1+ cos(2ω₀t+2φ₀)].(2.32) Согласно (2.32) W_pпотенциальная энергия, графическая зависимость которой на рис. 02.0.9 от величины отклонения Δy пружинного маятникаотносительно положения равновесия изображена короткимипунктирными линиями оранжевого цвета, минимальна в точке устойчивогоравновесия

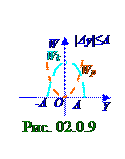
пружинного маятника, совпадающей сOначаломкоординат.

При максимальном отклонениипружинного маятникаотположенияравновесия, когда модуль |Δy| вектора Δy смещения равенамплитуде колебанийэтого пружинного маятника, т.е. |Δy| = y = A, потенциальнаяW_pэнергиясогласно (2.33) становитсяравной (mω₀ ²A²)/2. ПотенциальнаяW_pэнергия(2.32)пружинного маятникаизменяется с циклической2ω₀ (2.2) частотой в 2 раза превышающей ω₀ циклическуючастотупрямолинейных гармоническихколебаний (рис. 02.0.8) материальной точкиm массой.

КинетическаяW_kэнергия(1.88) из раздела 01.0.0 "Физические основы механики" материальной точки m массой, совершающей прямолинейные гармоническиеколебания по OY оси с учетом (2.9) ds/dt = dx/dt = v = - Aωsin(ωt+ φ₀) скорости смещенияэтойматериальной точки m массой в произвольный моментtвремени имеет следующий вид: W_k = mv²/2 = = (mω₀²A²/2) sin²(ω₀t+ φ₀) = (mω₀²A²/4)[1 - cos(2ω₀ t+2φ₀)] = = (mω₀²A²/2)[1 - cos²(ω₀t + φ₀)] = (mω₀²/2)(A² - y²).(2.33) Согласно (2.33)W_kкинетическаяэнергия, графическая зависимость которой на рис.2.9 от величины отклонения Δy пружинного маятникаотносительно положения равновесия изображена длиннымипунктирными линиями бирюзового цвета, максимальна в точке устойчивогоравновесия этого пружинного маятника, совпадающей с Oначаломкоординат.При максимальном отклонениипружинного маятникаотположенияравновесия, когда модуль |Δy| вектора Δy смещения равенамплитуде колебанийэтого пружинного маятника, т.е. |Δy| = y = A, кинетическаяW_k энергия согласно (2.33) становитсяравной нулю.