Вращающийся Aвектор, равный сумме векторов A1 иA2 , изображающих соответственногармонические колебания1 - го грузикаотносительно 2- го грузикаи гармонические колебания 4 страница

Волна называется сферической, если её волновые поверхностиимеют вид концентрических сфер. Центр этих сфер называется центром волны. Сферические волнывозбуждаются в однородной изотропной среде уединенным точечнымисточником. Уравнение расходящейся сферической волны,т.е. зависимость s=s(t) отклонений частиц упругой среды от положения равновесия впроизвольный моментt времени в функции r радиусасферической волновой поверхности в этой упругой средеимеет следующий вид: s = (a₀/r)cos(ωt - kr + φ₀), (2.76) где a₀/r - амплитудаколебаний частиц упругой среды, уменьшающаяся при удалениина r расстояние от центра источника или возбудителя сферическойволны; a₀ - физическая величина, численно равная амплитуде волнына единичномрасстоянии от её центра; φ₀ - начальная фазаколебаний в центре волны, а Ф = ωt - kr + φ₀ - фаза сферической волны.

Звуковые волны в газах

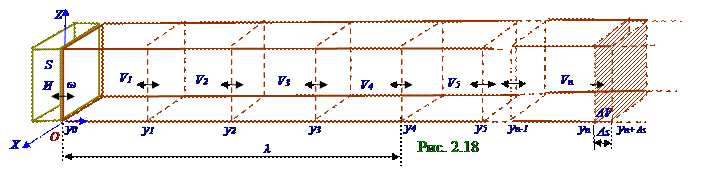
Звуковая волнав газе представляет собой распространяющуюся, например (рис.02.0.18) в трубе квадратногосечения, последовательность чередующихся областей сжатияи расширениягаза, т.е. продольную волну. Поэтому давлениев каждой точке пространства испытывает периодически изменяющееся ΔP отклонение от P среднего значения, совпадающего с давлением, которое существует в газе вотсутствие волн.

МгновенноеP^′ значение давленияв некоторой точке пространства имеет следующий вид: P^′ = P + ΔP. (2.77) Вследствие колебаний c (2.3) T = 2π/ω периодомгармонических колебаний (рис.2.18) внешнего И источника звука,например, мембраны,в длинном параллелипипеде V₁ объем газа, находящийся между сечениями газа с y₀, y₁ координатами, в интервал (рис.02.0.19) времени от 0 до T/4 испытывает сжатие( штриховка ) , вследствие чего область газаc y₀ координатой и S площадьюпоперечного сечения переместится в y₀ + s_m положение, т.е. в положение своего максимального отклоненияот положения равновесия и одновременно в этой области газамежду сечениями газа с y₀, y₁ координатами и S площадьюпоперечного сечения давление(2.77)достигнет своего P^′_max максимального значения.

Молекулы газа, приблизившись друг к другу,после T/4 момента времени начнут отталкиваться другот друга, вследствие чего V₁ объем газа в интервал времени от T/4 до T/2 испытывает растяжение(штриховка ) и приведет из-за наличия упругих сил к сжатию(штриховка )соседнего V₂ объёма, находящегося между сечениями газас y₁, y₂ координатами и т.д.

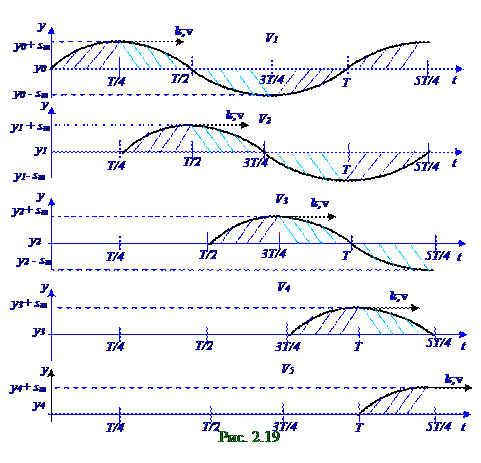
за T время с (2.68) фазовойvскоростьюраспространения волны в направлении k волнового вектора, перпендикулярного плоской волновой поверхности S площадью(рис. 02.0.18) поперечного сечения области газа.

Пусть в произвольный момент t времени (рис. 02.0.18) в сечении с y_n координатой V_n объёмгаза испытывает расширение на ΔVвеличину, вследствие чего его правая граньс y_n+1 координатой сместилась относительно своего положения равновесияна Δsрасстояние.

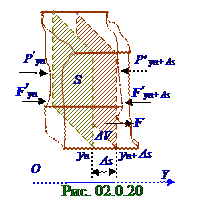
На рис. 02.0.20 изображено отдельно от всего газав (рис. 02.0.18) длинном параллелипипеде это приращениеΔV объёмагаза.Расширение газа, т.е. положительноеприращениеΔV объёма газа будет в том случае, если проекция F^'_yn на OY ось вектора F^′_yn силы давления газа, направленного перпендикулярно левой грани S площадью, по абсолютнойвеличине будет больше проекция F ^'_{yn+ Δs} на OY ось вектора F результирующейсилы на ΔV объёма газа будет иметь следующее положительное значение: - (|F ^'_{yn+ Δs}| - |F ^'_yn |) = - (|P'_{yn+ Δs} | -| P^′_yn| )S = F_y,(2.78) где знак "-" минус перед разностью абсолютныхвеличин (|F ^'_{yn+ Δs}| - |F ^'_yn|) проекцийсоответственно на левуюи правуюграни S площадью приращенияΔV объёма газа введён для получения

положительногозначения проекцияF_y на OY осьвектора F результирующейсилы ввиду того, что абсолютнаявеличинапроекции F ^'_yn на OY осьвектора F^′_nсилы давления на левуюгрань Sплощадьюпо абсолютнойвеличине будет больше проекции F ^'_{yn+ Δs} на OY осьвектора F ^'_{yn+ Δs} силы давления на правуюгрань той жеSплощадью.

В выражении (2.78) произведения P^′_yn, P^′_{yn+ Δs} давлений газасоответственнона левуюи правуюграни (рис. 02.0.20) ΔVобъёма газаS площадьюэтихгранейравны F ^'_yn, F ^'_{yn+ Δs} проекциям на OY ось

векторов F ^'_yn,F ^'_{yn+ Δs}, т.к.векторы F ^'_yn,F ^'_{yn+ Δs} сил давления газа перпендикулярны граням ΔVобъёма газа, а OY ось координат тоже перпендикулярна граням S площадью ΔVобъёма газа.

Приращение(2.78)ΔP′ = (|P' _{yn+ Δs}| -|P^′_yn|) давленияв ΔV объёме газа на (рис. 02.0.20) Δs длине имеет вид: ΔP′ = (∂P^′/∂y)Δs, вследствие чего проекцияF_y на OY осьвектора F результирующейсилы, действующей на ΔV объём газа Sплощадью и Δs длиной, имеет следующий вид: F_y = - (∂P^′/∂y)ΔsS.(2.79)

Волновое уравнение распространения акустических волн в однородной изотропной непоглощающей упругой среде: фазовая скорость распространения звука

В звуковой волне сжатиеи расширениегаза следуют друг за другом через короткие промежутки времени, вследствие чего смежныеучастки упругой средыне успевают обмениваться теплом. Поэтому связь между Pдавлениеми Vобъемом соседних участков газа, в котором распространяется акустическая волна, определяется законом Пуассона (4.68) из раздела 04.1.0 "Физическая термодинамика", имеющего следующий вид: PV^γ = const, (2.81) где γ - отношение молярнойC_pтеплоемкости газапри постоянномPдавлении к молярной

C_vтеплоемкости газа при постоянномV объеме. Уравнение (2.81) Пуассона для двух состояний газа: до возникновения упругойволны в газе с давлением (рис. 02.0.18) в V_n объеме и после возникновенияволны в газе, вследствие чего в

V_n + ΔV = S(Δy + Δs) объеме давление этого газа стало равным P^′, имеет следующий вид:

P(SΔy)^γ = P^′[S(Δy + Δs)]^γ = P^′{S[Δy + (∂s/∂y)Δy]}^γ = P^′(SΔy)^γ [1 + (∂s/∂y)]^γ ↔ ↔ P^′ = P/[1 + (∂s/∂y)]^γ ≈ P/[1 + γ (∂s/∂y)] ≈ P[1 - γ(∂s/∂y)], (2.82) где Δy- длина(рис. 02.0.18) V_nобъёма междусечениямис y_n и y_n+1 координатами.

Приближённые"≈" равенства в (2.82) выражении введены вследствие малости относительного отклонения, т.е.деформации(∂s/∂y) << 1 при s отклоненияхчастицот положения равновесияв произвольный момент t времени.В (2.82) сначала было использовано разложение выражения

[1 + (∂ s/∂y)]^γ в ряд по степеням (∂s/∂y) с пренебрежениемчленами высших порядков малости, а потом использовано приближенное равенство: 1/[1 + γ(∂s/∂y)] ≈ [1 - γ(∂s/∂y)], которое справедливо при γ(∂s/∂x) << 1.

Первая производнаяот выражения(2.82) по y имеет следующий вид:

∂P^′/∂y = -γP(∂²s/∂y²).(2.83) Подставляем (2.80) в (2.82) и получаем следующее одномерное волновое уравнениераспространения акустических волнвлинейной однородной изотропной непоглощающей упругой среде: ∂²s/∂y² = ρ(∂²s/∂t²)/γp ↔ ∂²s/∂y² = (1/v²)(∂²s/∂t²), (2.84) где (γP/ρ)^1/2 = v- фазовая(рис. 02.0.18), (рис. 02.0.19) скоростьраспространения звуковойволны в направлении k волнового вектора, перпендикулярного плоской волновой поверхности S площадьюпоперечного сечения области газа.

Из уравнения Менделеева - Клапейрона (4.13) из раздела 04.1.0 "Физическая термодинамика" для идеальногогаза при постоянномpдавлении имеет место следующее выражение: P/ρ =RT/μ ↔ ρ = Pμ/RT, (2.85) где R - универсальная газовая постоянная; T - термодинамическая температура; μ - масса одного моля газа; ρ - плотностьэтогогаза.

Подставляем (2.85) ρ плотностив выражение (2.84),после чегофазоваяv скоростьраспространения звуковойволны в газев принимает следующий вид: v = (γRT/μ)^1/2. (2.86)

Средняя<v>скоростьтеплового движения молекул газа(4.268) из раздела 04.2.0 "Физическая термодинамика"имеет следующий вид: <v>= (8RT/πμ)^1/2.(2.87) Сравнивая (2.86) и (2.87) получаем следующее соотношениефазовойvскоростираспространения звуковойволны в газесо средней<v>скоростью теплового движения молекул газа: v = <v>(γπ /8)^1/2 ≈ (3/4)<v>. (2.88) Согласно (2.88) фазовая vскоростьраспространения звуковойволны в газеодного порядка со средней<v>скоростью теплового движения молекул газа.

По аналогии с одномерным(2.85)волновым уравнениемраспространение акустических волнвлинейной однородной изотропной непоглощающей упругой среде с учетомsотклоненияот положения равновесия частицэтой среды в произвольный моментt времени в произвольной точке трехмерного пространствас декартовымиx,y и z координатами описывается следующим трёхмерным волновымуравнением: (∂²s/∂x²) + (∂²s/∂y²) + (∂²s/∂z²) = (1/v²)(∂²s/∂t²),(2.89) гдеvфазовая скоростьраспространения звуковойволны в любом направлении трёхмерного пространства вследствие свойства изотропностиэтого пространства и любой точке с

x,y и z координатамивследствие однородности трёхмерного пространства.

Волновое уравнение, фазовая скорость распространения продольных упругих волн в стержнях

Фазоваяvскоростьраспространения продольной упругой волны в тонком стержне определяется из волнового уравнение распространения этих упругих продольныхволн в тонких стержнях, когда ød диаметр (рис. 02.0.21) стержня много меньше λ длины упругой волны, т.е. когда ød<< λ.

Упругая продольнаяволна в тонком стержне по аналогии(рис. 02.0.18) с звуковой волнойв газе представляет собой (рис. 02.0.21) последовательность чередующихся областей (синий цвет)сжатияи (голубой цвет) расширения, распространяющихся в направлении k волнового вектора, т.е. вдоль оси этого тонкого стержняв положительную сторону OY оси. Вследствие колебаний c (2.3)

T = 2π/ω периодомгармонических колебаний (рис. 02.0.21) внешнего И источника звука,например, пьезоэлектрического вибратора,V₁ объем тонкого стержня, находящегося между сечениями газа с y₀, y₁ координатами, в интервал (рис.2.21) времени от 0 до T/4 испытывает (синий цвет) сжатие.

В интервал (рис. 02.0.21) времени от T/4 до T/2 объем V₁ тонкого стержняиспытывает

(голубой цвет) расширение, вследствие чего малый объем тонкого стержняΔy длиной, находящийся в начальный момент t₀ = 0 времени в (серый цвет) недеформированном состоянии, расширяется на малую Δs длину. Поэтому этот малый объем тонкого стержняΔy длиной к моменту T/2 времени имеет

∂s/∂y относительную деформацию, которая определяется следующим предельным переходом от малой

Δy длины тонкого стержня, который получил малую Δs деформацию: ε = limΔs/Δy = ∂s/∂y,(2.90) Δy→0

где ε = ∂s/∂y - относительная деформация численно равна значению длины, на которую расширился или сжался рассматриваемый объем тонкого стержняпри распространении в нём упругих продольныхволн, отнесённой к длине этого тонкого стержня. При расширении объема тонкого стержня ε = ∂s/∂y относительная деформация больше нуля, т.к. (2.90) при расширении Δs > 0. Присжатии объема тонкого стержня ε = ∂s/∂y относительная деформация меньше нуля, т.к. (2.90) при сжатии Δs < 0.

При малых продольныхдеформациях рассматриваемый объем тонкого стержняхарактеризуетсяσнапряжением,котороесогласнозакону Гука имеет следующее выражение:

σ = Eε,(2.91)

где E, Н/м² - модуль Юнга, характеризующий прочностные свойства тонкого стержня, а именно, равный силе, которую надо приложить к тонкому стержню с единичнымпоперечным сечением, чтобы ε относительная деформация в нём равнялась единице, т.е. когда (2.90) малая Δy длина недеформированного стержня под воздействием приложенной силы увеличилась на величину малой

Δs = Δy деформации; σ, Н/м² - напряжение в площади поперечного сечения тонкого стержня, расположенной в y координате; напряжение σ, Н/м² численно равно результирующей силе, приложенной в данной y координате к единичной площади поперечного сечения тонкого стержняс

вектором этой результирующей силы, направленным перпендикулярно поперечному сечению тонкого стержня;напряжение σ, Н/м² в площади поперечного сечения тонкого стержня, расположенным в

y координате тонкого стержня, имеет знак ε относительной деформации в этой площади поперечного сечения тонкого стержня:при расширении объема в данной площади поперечного сечения тонкого стержня ε = ∂s/∂y относительная деформация (2.90) больше нуля, поэтому напряжение σ, Н/м² в этой площади тоже больше нуля;при сжатии объема в данной площади поперечного сечения тонкогостержня ε = ∂s/∂y относительная деформация (2.90) меньше нуля, поэтому напряжение σ, Н/м² в этой площади тоже меньше нуля.

На рис. 02.0.22 по аналогии с рис. 02.0.20, где изображеноприращениеΔV объёмагаза при распространении в нём звуковой волны,представлен отдельно от всего (рис.2.21) тонкого стержнямалый ΔV объем этого тонкого стержняΔs длиной и S площадью поперечного сечения, испытывающий в момент t_n времени расширение.

При расширении малого ΔV объема тонкого стержня к правой чёрной стенке приложен вектор F_{yn+ Δs} силы упругой деформации в положительном направлении OY оси, вследствие чего эта правая чёрная стенка удалиласьот левой зелёнойстенки малого ΔV объема тонкого стержня на малую

Δs длину и заняла положение с y_n+ Δs координатой. К левой зелёнойстенке малого ΔV объема тонкого стержня, имеющей внедеформированном состоянии y_n координату, приложенвектор F _yn силы упругой деформации, который противодействует вектору F_{yn+ Δs} силы упругой деформации в

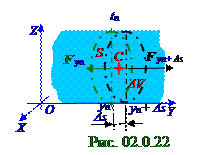
деформации в правой чёрнойстенки с y_n+ Δs координатой, а F _yn модуль вектора F _yn силы упругой деформации у левой зелёнойстенки малого ΔV объема меньше F_{yn+ Δs} модуля вектору F_{yn+ Δs} силы упругой деформации в правой чёрнойстенки с y_n+ Δs координатой, потому что в противном случае не происходило бы расширения малого ΔV объема на Δs длину в положительном направлении OY оси.

Проекция II закона Ньютонана OY осьдля m массы материала тонкого стержня

ρплотностью, заключённой в (рис.2.22) малом объема ΔV=SΔs, к которой по OY оси приложены два вектора: вектор F_{yn+ Δs} силы упругой деформации в правой чёрнойстенки с y_n+ Δs координатой и вектор F _yn силы упругой деформации у левой зелёнойстенки с y_n координатой, имеет следующий вид: OY: ρSΔs(∂²s/∂t²) = (F_{yn+ Δs})_y + (F_yn)_y = F_{yn+ Δs} - |F_yn|,(2.92)

где ∂²s/∂t² - проекция вектора ∂²s/∂t² ускоренияна OY ось (рис.2.22) центраC масс малого ΔV объема тонкого стержняпри его расширениина Δs длину в положительном направлении OY оси;

(F_{yn+ Δs})_y = F_{yn+ Δs} - проекция на OY ось вектора F_{yn+ Δs} силы упругой деформации, который направлен в положительную сторону OY оси; (F_yn)_y = - |F_yn|- проекция на OY ось вектора F_yn силы упругой деформации, который направлен в отрицательную сторону OY оси, что в (2.93) учтено знаком "-" минус перед |F_yn| модулемэтого вектора F_yn силы упругой деформации.