Временнаяsin(ωt - kL ) часть (2.122) уравнения не зависит от y координаты и определяет состояние всех частиц упругой среды вданный моментtвремени. Например, в момент

tвремени, когда sin(ωt - kL ) временнаячасть (2.123) уравнения равна нулю, все частицы имеют

s смещение частиц упругой средыот положения равновесия, равное нулю. В моментtвремени, когда sin(ωt - kL ) временнаячасть (2.122) уравнения равна единице, все частицы имеют s смещение частиц упругой средыот положения равновесия, равноеамплитуде, т.е. максимальномузначению. В отличии отбегущей(2.118) акустической волны в стоячей акустической волне существуют волновые поверхности с y_у координатами, в которых движение частиц упругой средыотсутствует. Координаты y_уволновых поверхностей, в которых движение частиц упругой средыотсутствует, называется узлами стоячей волны.

В стоячей плоской акустической волны существуют волновые поверхности с y_п координатами, в которых в определённые моментыtвремени смещение частиц упругой среды относительно своего положения равновесия достигает максимума.Координаты y_п, в которых в определённые моментыtвремени частицы упругой среды достигают своего максимальногозначения, называются пучностями.

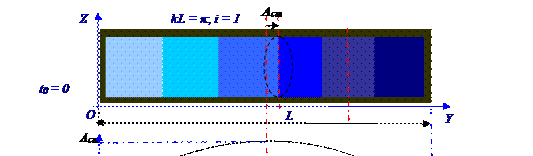
В области упругой среды, находящейся вблизи волновых поверхностей с y_п координатами пучностейсуществуют в определённые моментыtвремени (2.104) максимальныезначения скорости частиц этой упругой среды, поэтому в упругой среде сy_пкоординатами пучностейчастицы упругой средыимеютмаксимальноезначениеW_kкинетической энергии. Если (рис. 02.0.27) длина L закрытой с правойстороны трубы, в которойс помощью вибраторау левой открытой стороны трубы возбуждаетсяакустическая волна, такова, что k₁ L = π/2, где (2.70) k₁ = 2π/λ₁ – волновоечисло, то в t = nT/2 моменты времени, где n = 0, 1, 2, …, а T - период колебанийисточникаакустической волны, т.е. вибратора, модуль sin(ω₀t - kL ) временнойчасти (2.122) уравнения равен единицеи s отклонениячастиц от положения равновесиявy координате упругой среды, равной нулю, т.е.y = 0, будут равны A_ст амплитуде стоячей акустической волны, равной удвоеннойамплитудеэтих частиц упругой средыв режиме (2.69) бегущей акустической волны, т.е. A_ст = 2A.

В интервал (рис. 02.0.27) времени от t₀ = 0 с до t₂ = T/2 с падающая(2.118) волна s₁ = s₁(y, t) распространяется от И источника, т.е. вибратора, до закрытой с правойстороны трубы, затем отражается от этой закрытой стороны трубы с изменением фазыотражённой акустической волнынавеличину, равнуюπ,и возвращается к моменту t₂ = T/2 с времени в сечение трубы с y = 0 координатойy = 0 по OY оси. В этом сечении отраженная (2.121) волна s₂ = s₂(x, t) с отрицательным смещением частиц упругой среды относительно положения равновесия, равным "-A", складывается с таким же смещением, равным "-A", у И источника(2.118)падающей волны s₁ = s₁(x, t), вследствие чего в сечении с 0 координатой по OY осив момент t = T/2 с временирезультирующие отклонения(2.122) s = s(x, t) частиц упругой средыот положенияравновесия в открытой части трубы будут максимальныв сторону, противоположную OY оси, т.е. при y = 0, будут равныотрицательным

"- A_ст = -2A" смещениям частиц упругой среды относительно положения равновесия. Интервал времени от t = 0 c до t = T/2 с является интервалом, в пределах которого происходит установлениерезультирующих отклонений(2.123)s = s(x, t) частиц упругой средыот положенияравновесия в режиме стоячей волны.

Если длина L закрытой с однойстороны трубытакова, что k₁L = π/2, то на открытойстороне трубы устанавливается пучность стоячей плоской акустической волны, а у закрытой стороны трубы устанавливается узелэтой стоячей плоской акустической волны. Такие же, что и в момент t = T/2 с времени результирующие отклонения(2.122)s = s(x, t) частиц упругой средыот положенияравновесиябудут иметь в моменты t = 3T/2; 5T/2;…с времени, т.е. эти отклонения будут равныотрицательным"- A_ст = -2A" смещениям частиц упругой среды относительно своего положения равновесия.

В моменты времени t = T, 2T, …с, представленные на рис. 02.0.27 результирующие(2.122) отклоненияs = s(x, t) частиц упругой средыот положенияравновесия в открытой части трубы будут максимальныв направлении OY оси, т.е. при y = 0, будут равны (2.122) удвоенной Aамплитуде

A_ст = 2Aбегущей волны.

Приращение Δp′давления(2.77),если (рис. 02.0.27) L длина закрытой трубы такова, что

k₁L = π/2, в упругой средев сечении трубы, где y = 0, т.е. в её открытойчасти, будет равно нулю, т. к. эта часть трубы находится в открытомпространстве. В сечении закрытой части трубы, т.е. при y = L, приращение Δp′давлениябудет максимально: либо разрежение, которое возникнет в моменты

t = (2n + 1)T/2 с времени, где n = 0,1,2,…, и обозначены на рис. 02.0.27 бледно-голубым цветом, либо сжатие, которое возникнет в моменты t = 2nT/2 с времени, где n = 0,1,2,…, и обозначены на рис. 02.0.27 тёмно-синим цветом.

Таким образом, если L длина закрытой с однойстороны трубы такова, что k₁L = π/2, то на открытойстороне трубы устанавливается узел давления стоячей плоской акустической волны, а у закрытой стороны трубы устанавливается пучность давления этой стоячей плоской акустической волны.

Графики на рис. 02.0.27 при k₁L = π/2относятся к стоячейволне, существующей в закрытой с правой стороны трубе, когда её L длина равна четвертиλ₁/4 длины бегущейволны, т.е. имеет место следующее выражение: L = λ₁/4, (2.123) где λ₁ - длина первой гармоники бегущейволны.

При выполнении условия (2.124) на Lдлине закрытой с правой стороны трубы укладывается четвёртаячасть от всей λ₁ длины бегущей волны.

Длина λ_1ст /2 первойгармоники стоячейволны, которая измеряется (рис. 02.0.27) по расстоянию между двумя соседними узлами или между двумя соседними пучностямиэтой стоячейволны, при выполнении условия(2.124) имеет следующий вид: λ_1ст= λ₁ /2 = 2L.(2.124)

Согласно (2.12) длина λ_ст стоячейволны в 2 раза меньшеλ длины бегущейволны. Если

L длина закрытой трубы такова, что k₂L = 3π/2, то (рис. 02.0.28) на L длине закрытой с правой стороны трубы укладывается три четвёртыхчасти от всей λ₁ длины бегущей волны второйгармоники и с учётом (2.124) три вторыхчасти от всей λ_2ст длины второйгармоники стоячей волны.

В этом случае имеет место следующее выражение: L = 3λ₂/4 = 3λ_2ст/2 ↔ λ_2ст = 2L/3, (2.125) где λ_2ст - длина второй гармоники стоячейволны.

Таким образом, при выполнении следующего условия: k_iL = (2i - 1)π/2, (2.126) где i = 1, 2, 3…; k_i = 2π/λ_i – волновоечисло; в закрытой с правой стороны трубе L длиной возникают стоячиеволныпервой, второй, третьейи т.д. гармоник, длины волн λ_1ст, λ_2ст, λ_3ст, … и

λ₁, λ₂, λ₃, … которых определяютсяиз следующих выражений:

(2π/λ_i )L = (2i - 1)π/2 ↔ λ_i =4L/(2i - 1) ↔ λ_iст =2L/(2i - 1), (2.127) где λ_i - длины бегущейволны соответствующие своему iномеру гармоники; λ_iст =λ_i /2 - длины стоячейволны соответствующие своему iномеру гармоники.

от положенияравновесия отсутствует, т.е. на левой и правой частях трубы существуют узлы стоячейволны.

Приравнивание - 2Asink(L - y) амплитудной части (2.122) уравнения нулюпри y = 0 позволяет получить следующее выражение для определения λ_i длины бегущей акустическойволны и λ_iст =λ_i /2 длины стоячей акустической волны, соответствующих своему iномеру гармоники и

возникающих в трубе с двухконцов закрытой упругой средойболее плотной, чем упругая среда внутри трубы:

- 2Asink_i(L - y) = 0 ↔ sink_iL = 0 ↔ k_iL = iπ ↔ (2π/λ_i)L = iπ ↔ λ_i=2L/i ↔ λ_iст =L/i, (2.128) где i = 1, 2, … - номер гармоники; λ_i - длина i - ой гармоники бегущей волны, λ_iст - длина i - ойгармоники стоячейволны, соответствующей i - ойгармоники бегущейволны.

Стоячая волна в непоглощающей упругой среде: расчёт координат узлов и пучностей

На первой гармонике стоячейволны (рис. 02.0.27) в закрытой с правой стороны трубе, т.е. когда i = 1, λ_1ст длина волны этой стоячейволны (2.128) равна 2L (рис. 02.0.27), а соответствующая этой стоячейволне бегущаяволна имеет λ₁ длину 4L, в сечении закрытой трубы с y = L координатой, т.е. у закрытой стенкитрубы, согласно (2.122) отклоненияs = s(y, t) частиц упругой средыот положенияравновесия будет в любой момент времени равны нулю. Эта y = L координата является y_y0 координатой узла для этой первой гармоники стоячейволны.

Общее выражение y_ym координат (рис.2.27) узлов в закрытой с правой стороны трубе, где m = 0, 1, 2, …номер узла для первой, второй, третьей и т.д. …гармоник стоячих волн с длинами λ_1ст, λ_2ст, λ_3ст, …,cоответствующих длинам λ₁, λ₂, λ₃, …бегущих волн, выводится приравниванием- 2Asink(L - y) амплитудной части (2.122) уравнения нулю.

Координаты узлов y_ym в закрытой с правой стороны трубе определяются с учётом (2.127)

λ_i =4L/(2i - 1) длины бегущей волны и (2.70) k_i = 2π/λ_i волновогочисло из следующего выражения:

- 2Asink_i(L - y_ym ) = - 2Asin[(2π/λ_i)(L - y_ym )] = - 2Asin{2π[(2i + 1)/4L](L - y_ym )} = 0 ↔

↔ 2π[(2i + 1)/4L](L - y_ym ) = mπ ↔ y_ym = L{1 - [2m/(2i -1)]}, (2.129)гдеm= 0, 1, 2, … номер узла для первой, второй, третьей и т.д. … гармоники, а m_max максимальное значение номера узла равно i - 1 номеру гармоникиэтой стоячейволны; k_i =2π/λ_i= π(2i - 1)/4L – волновое число (2.70), при выводе которого использовано выражение (2.128) для λ_i длины бегущейволныпервой, второй, третьей и т.д. гармоник. Согласно (2.128) для первой гармоники стоячейволны, т.е. при i = 1, с λ_1ст длинойстоячей волны, равной 2L, которой соответствует λ₁ длина бегущейволны, равная 4L, существует один узел (рис. 02.0.27) этой стоячейволны с координатой (2.128) y_y0 = L при m_max = i - 1 = 0.

Для (рис. 02.0.28) второй гармоники стоячейволны, т.е. при i = 2, с λ_2ст длиной стоячей волны, равной (2.127) λ_2ст = 2L/3, которой соответствует λ₂ длина бегущейволны, равная λ₂ =4L/3, существуют (2.129) два узла этой стоячейволны со следующими координатами: y_y0 = L при m = 0; y_y1 = L/3 при m_max = i - 1 = 1.(2.130) Для третьей гармоники стоячейволны, т.е. i = 3, с λ_3ст длиной стоячей волной, равной (2.127)λ_3ст = 2L/5, которой соответствует λ₃ длина бегущейволны, равная λ₃ =4L/5, волны существует (2.129) три узла этой стоячейволны со следующими координатами:

y_y0 = L при m = 0; y_y1 = 3L/5 при m = 1; y_y2 = L/5 при m_max = i - 1 = 2.(2.131) Общее выражение y_ym координат (рис. 02.0.29) узлов закрытой с двухконцов трубы, где

m = 0, 1, 2, …номер узла для первой, второй, третьей и т.д. …гармоник стоячих волн с длинами λ_1ст, λ_2ст, λ_3ст, …,cоответствующих (2.124) длинам λ₁, λ₂, λ₃, …бегущих волн, выводится приравниванием- 2Asink(L - y) амплитудной части (2.122) уравнения нулю.

Координаты узлов y_ym определяются с учётом (2.128) λ_i=2L/i длины бегущей волны и (2.70)

k_i = 2π/λ_i волновогочисла из следующего выражения:

- 2Asink_i(L - y_ym ) = - 2Asin[(2π/λ_i)(L - y_ym )] = - 2Asin(2πi/2L)(L - y_ym ) = 0 ↔

↔ 2π(i/L](L - y_ym ) = mπ ↔ y_ym = L[1 - (m/i)], (2.132)гдеm= 0, 1, 2, … номер узла для первой, второй, третьей и т.д. … гармоник, а m_max максимальное значение номера узла равно i номеру гармоникиэтой стоячейволны; k_i =2π/λ_i= πi/L – волновое число (2.70), при выводе которого использовано выражение (2.128) для λ_i длины бегущейволныпервой, второй, третьей и т.д. гармоник.

Согласно (2.132) для (рис. 02.0.29) первой гармоники стоячейволны в закрытой с двухконцов трубы, т.е. i = 1, с λ_1ст длинойстоячей волны, равной L, которой соответствует λ₁ длина бегущейволны, равная (2.124) 2L, существует два узла этой стоячейволны с y_y0 = L координатой (2.132)при

m = 0 и y_y1 = 0 координатой при m_max = i = 1.

В начальный момент t₀ = 0 времени для (рис. 02.0.29) первой гармоники стоячейволнырезультирующие(2.122) отклоненияs = s(y, t) частиц упругой средыот положенияравновесия в центре трубы будут максимальныв направлении OY оси, т.е. при y = 0, будут равны (2.122) удвоенной AамплитудеA_ст = 2Aбегущей волны, т.е. в центре этой трубы будет пучность стоячейволны.

Приращение Δp′давления(2.77),если L длина (рис. 02.0.29) закрытой с двухконцов трубы такова, что k₀L = π, в упругой средев сечении трубы, где y = 0, т.е. у её левогоконца, будет отрицательно и равно по модулю максимальному A_Δp′ отклонению давления частиц упругой средыотравновесного значения. Отрицательное приращение Δp′давления, т.е. растяжение,у левогоконца закрытой с двухконцов трубы обозначено на рис. 02.0.29 бледно-голубым цветом.

В сечении трубы, где y = L, т.е. у её правогоконца, приращение Δp′давления(2.78) будет положительно и равно A_Δp′ максимальномуотклонению давления частиц упругой средыотравновесного значения. Положительное приращение Δp′давления, т.е. сжатие,у правогоконца закрытой с двухконцов трубы обозначено на рис. 02.0.29 тёмно-синим цветом.

Таким образом, если L длина (рис. 02.0.29) закрытой с двухконцов трубы такова, что k₁L = π, то на закрытыхсторонах трубы устанавливаются пучности давления стоячей плоской акустической волны, а в центре трубы устанавливается узел давления этой стоячей плоской акустической волны.

Для (рис. 02.0.30) второй гармоники стоячейволны в закрытой с двухконцов трубы, т.е. i = 2, с λ_2ст длиной стоячей волной, равной (2.124) λ_2ст = L/2, которой соответствует λ₂ длина бегущейволны, равная λ₂= L, существует (2.132) три узла этой стоячейволны со следующими координатами: y_y0 = L при m = 0; y_y1 = L/2 при m = 1; y_y1 = 0 при m = i = 2.(2.133)

В начальный момент t₀ = 0 времени для (рис.2.29) первой гармоники стоячейволнырезультирующие(2.122) отклоненияs = s(y, t) частиц упругой средыот положенияравновесия в центре закрытой с двухконцов трубы будет равнымнулю, т.е. в центре этой трубы будет узел стоячейволны.

Пучности результирующего(2.123) отклоненияs = s(y, t) частиц упругой средыот положенияравновесия встоячейволны, равные удвоенной AамплитудеA_ст = 2Aбегущей волны, будут располагаться в y_п = L/4, y_п = 3L/4 координатах закрытой с двух концовтрубы.

A_Δp′ максимальному отклонению давления частиц упругой средыотравновесного значения, т.е.упругая средана закрытых концах трубы будет испытыватьсжатие, которое обозначено на

рис. 02.0.30 тёмно-синим цветом.

В начальный момент t₀ = 0 времени для (рис. 02.0.30) второй гармоники стоячейволны в центре закрытой с двух концов трубы приращение Δp′давления(2.77) будет отрицательно и равно по модулю максимальному A_Δp′ отклонению давления частиц упругой средыотравновесного значения, т.е.упругая средав центре закрытой с двухконцов трубы будет испытыватьрастяжение, которое обозначено на рис. 02.0.30 бледно-голубым цветом.

В последующие моменты t времени стоячейволны в закрытой с двухконцов трубе

y координатыузлов приращения Δp′давленияирезультирующего отклоненияs = s(y, t) частиц упругой средыот положенияравновесияостанyтся неизменными. Координаты пучностей приращения Δp′давления и результирующего отклоненияs = s(y, t) частиц упругой средыот положенияравновесиятоже останутся неизменными, но через T_i/2 половинупериодаколебаний частиц упругой среды в режиме стоячейволны i - ой гармоники знаки отклоненийs = s(y, t) частиц упругой средыот положенияравновесияиприращения Δp′давления изменятся напротивоположные,т.е. положительныесмещения частиц упругой среды относительно положенияравновесиястанут отрицательными, а положительные приращения Δp′давления стоячей плоской акустической волныпревратятся в отрицательные.

Общее выражение координат пучностейy_пm для (рис. 02.0.27), (рис. 02.0.28)закрытой с однойстороны трубы, где m= 0, 1, 2, …номер пучностидля первой, второй, третьей и т.д. … гармоник стоячих волн с длинами λ_1ст, λ_2ст, λ_3ст, …, соответствующих (2.124) длинам λ₁, λ₂, λ₃, …бегущих волн, которые употребляются в уравнении стоячей волны,выводится приравниванием - 2Asink(L - y) амплитудной части (2.122) уравнения величине 2A, т.е.максимальномуотклонениюs = s(y, t) частиц упругой средыот положенияравновесия, вследствие чего имеет место следующее выражение:-2Asink_i(L - y_пm ) = -2Asin{2π[(2i - 1)/4L](L - y_пm)} = ±2A ↔

↔ 2π[(2i - 1)/4L] (L - y_пm) = (2m + 1)π/2 ↔ y_пm = L{1 - [(2m+1)/(2i-1)]}, (2.134) гдеm = 0, 1, 2, … номер пучностидля первой, второй, третьей и т.д. … гармоник стоячейволны, а

m_max максимальное значение номера пучности равно i -1 номеру гармоникиэтойстоячейволны;

k_i =2π/λ_i = π(2i - 1)/4L - волновое число (2.70), при выводе которого использовано (2.127) выражение для λ_i длины бегущейволныпервой, второй, третьей и т.д. гармоник. Для первой гармоники стоячейволны, т.е. при i = 1, с λ_1ст длиной стоячей волной, равной

λ_1ст = 2L, которой соответствует λ₁ длина бегущейволны, равная (2.128) λ₁=4L, существует

(рис. 02.0.27) одна пучность этой стоячейволны с (2.134) координатой, равной y_п0 = 0 при

m_max = i - 1 = 0.

Для второй гармоники стоячейволны, т.е. при i = 2, с λ_2ст длиной стоячей волной, равной

λ_2ст = 2L/3, которой соответствует λ₂ длина бегущейволны, равная (2.127) λ₂ =4L/3, существуют

(рис. 02.0.28) двепучности этой стоячейволны со (2.134) следующими координатами: y_п0 = 2L/3 при m= 0; y_п1 = 0 при m_max = i - 1 = 1.(2.135)

Общее выражение координат пучностейy_пm для (рис. 02.0.29), (рис. 02.0.30) закрытой с двухконцов трубы, где m = 0, 1, 2, …номер пучностидля первой, второй, третьей и т.д. … гармоник стоячих волн с длинами λ_1ст, λ_2ст, λ_3ст, …, соответствующих (2.124) длинам λ₁, λ₂, λ₃, …бегущих волн, которые употребляются в уравнении стоячей волны,выводится приравниванием - 2Asink(L - y) амплитудной части (2.122) уравнения величине 2A, т.е.максимальномуотклонениюs = s(y, t) частиц упругой средыот положенияравновесия, вследствие чего имеет место следующее выражение:

-2Asink_i(L - y_пm ) = -2Asin(2π i/2L)(L - y_пm)} = ±2A ↔ (πi/L)(L - y_пm) = (2m + 1)π/2 ↔

↔ y_пm = L[1 - (2m+1)/2i], (2.136) гдеm = 0, 1, 2, … номер пучностидля первой, второй, третьей и т.д. … гармоник стоячейволны, а

m_max максимальное значение номера пучности равно i -1 номеру гармоникиэтойстоячейволны;

k_i =2π/λ_i = πi/L - волновое число (2.70), при выводе которого использовано (2.128) выражение для

λ_i длины бегущейволныпервой, второй, третьей и т.д. гармоник. Для первой гармоники стоячейволны, т.е. при i = 1, с λ_1ст длиной стоячей волной, равной

λ_1ст = 2L, которой соответствует λ₁ длина бегущейволны, равная (2.128) λ₁=2L, существует

(рис. 02.0.29) одна пучность этой стоячейволны с (2.136) координатой, равной y_п0 = L/2 при

m_max = i - 1 = 0.

Для второй гармоники стоячейволны, т.е. при i = 2, с λ_2ст длиной стоячей волной, равной

λ_2ст = L, которой соответствует λ₂ длина бегущейволны, равная (2.128) λ₂ =2L, существуют

(рис. 02.0.30) двепучности этой стоячейволны со (2.136) следующими координатами: y_п0 = 3L/4 при m= 0; y_п1 = L/4 при m_max = i - 1 = 1.(2.137)

Стоячая волна в непоглощающей упругой среде: уравнения скорости смещений и относительной деформации частиц упругой среды относительно положений равновесия

Первая ∂s/∂t производная (2.122) по t времени отклоненияs = s(y, t) частиц упругой средыот положенияравновесия в режиме стоячейволны (рис. 02.0.27) в закрытой с правой стороны трубе характеризует скорость смещения этих частиц упругой среды в произвольные моменты t времени и в произвольной y координате, вследствие чего имеет место следующее выражение для этой первой

∂s/∂t производной по t времени: ∂s/∂t = - 2Aω_isink_i(L - y)cos(ω_it - k_iL),(2.138)где ω_i = 2πv/λ_i - циклическая(2.70) частота колебаний частиц упругой среды в режиме стоячейволны i - ой гармоники, имеющей (2.128) λ_i длину бегущейволны.

При подстановке в sink_i(L - y) амплитуднойчасти (2.138) выражения ∂s/∂t первой производной по t времени(2.122) отклоненияs = s(y, t) частиц упругой средыот положенияравновесия, например,

(рис. 02.0.27) в закрытой с правой стороны трубе в режиме стоячейволны волновогоk_i =2π/λ_i числа и λ_i =4L/(2i - 1) длины (2.129) i - ой гармоники бегущейволны, а также координат y_ym (2.129)узлов стоячей волны, эта sink_i(L - y) амплитуднаячастьвыражения (2.136) превращается в ноль. Это соответствует свойствам стоячейволны, а именно в узлах этой стоячей волны s = s(y, t) смещения частиц упругой среды относительно положения равновесияв произвольный момент t времени отсутствуют, т.е. ∂s/∂t скорость смещения этих частиц упругой среды в произвольные моменты

t времени в узлах стоячей волны равны нулю.

При подстановке в sink_i(L - y) амплитуднойчасти (2.138) выражения ∂s/∂t первой производной по t времени(2.122) отклоненияs = s(y, t) частиц упругой средыот положенияравновесия в режиме стоячейволны волновогоk_i =2π/λ_i числа и λ_i =4L/(2i - 1) длины (2.127) i - ой гармоники бегущейволны, а также y_пm координат (2.134)пучностей стоячей волны, эта sink_i(L - y) амплитуднаячастьвыражения (2.137) превращается в единицу. Поэтому в пучностях стоячейволны ∂s/∂t скорость

s смещения частиц упругой средыот положенияравновесия в режиме (2.122) стоячейволны максимальны и имеют амплитуду (2.137) этих отклонений, равную 2Aω_i.

Первая ∂s/∂y производная по y координате(2.122) отклоненияs = s(y, t) частиц упругой средыот положенияравновесия в режиме стоячейволны (рис. 02.0.27) в закрытой с правой стороны трубе характеризует (2.91) ε = ∂s/∂y относительную деформацию этой упругой среды, которая численно равна значению длины, на которую расширился или сжался рассматриваемый объем упругой средыпри распространении в нём продольнойволны, отнесённый к длины этого объема упругой среды, вследствие чего имеет место следующее выражение для этой первой ∂s/∂y производной по y координате: ∂s/∂y = - 2k_iAcosk_i(L - y) sin(ω_it - k_iL ),(2.139) где ω_i = 2πv/λ_i - циклическая(2.70) частота колебаний частиц упругой среды в режиме стоячейволны i - ой гармоники, имеющей (2.128) λ_i длину бегущейволны.

При подстановке в cosk_i(L - y) амплитуднойчасти (2.139) выражения ∂s/∂y первой производной по y координате(2.122) отклоненияs = s(y, t) частиц упругой средыот положенияравновесия, например, (рис. 02.0.27) в закрытой с правой стороны трубе в режиме стоячейволны волнового

k_i =2π/λ_i числа и λ_i =4L/(2i - 1) длины (2.127) i - ой гармоники бегущейволны, а также координат y_ym (2.129)узлов стоячей волны, эта cosk_i(L - y) амплитуднаячастьвыражения (2.139) превращается в единицу. Поэтому в узлах стоячейволны (2.90) ε = ∂s/∂yотносительная деформация упругой среды максимальна и имеет амплитуду, равную (2.139) 2Ak_i.

При подстановке в cosk_i(L - y) амплитуднойчасти (2.139) выражения ∂s/∂y первой производной по y координате(2.122) отклоненияs = s(y, t) частиц упругой средыот положенияравновесия в режиме стоячейволны волновогоk_i =2π/λ_i числа и λ_i =4L/(2i - 1) длины (2.127) i - ой гармоники бегущейволны, а также координат y_пm (2.134)пучностей стоячей волны, эта cosk_i(L - y) амплитуднаячастьвыражения (2.139) превращается в нулю. Поэтому в пучностях стоячейволны (2.90) ε = ∂s/∂yотносительная деформация упругой среды отсутствует.