Вращающийся Aвектор, равный сумме векторов A1 иA2 , изображающих соответственногармонические колебания1 - го грузикаотносительно 2- го грузикаи гармонические колебания 6 страница
Выполнение равенства (2.112) в точке упругой среды с y координатой в данныймомент
t времени возможно, если ω1 и ω2 циклические частоты гармонических (рис. 02.0.16) колебаний в упругойсредеот соответственно И1 и И2 источниковкогерентных(2.20) колебаний равны друг другу, т.е. когда выполняется следующее соотношение: ω1 = ω2 = ω. (2.112) Интерференциейволн называется явление наложения волн, при котором существует устойчивое во tвремени их взаимное усиление в одних точках пространства и ослаблениев других точках пространства в зависимости от соотношения между фазамиэтих волн. Интерферироватьмогут только когерентныеволны, которые распространяются вдоль одного и того же или близких направлений.
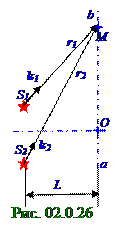
При наложении когерентных сферическихволн, возбуждаемых точечными (рис. 02.0.26)
S1, S2 источникамигармонических колебаний, отклонения соответственноs1 = s1(r1, t) , s2 = s2(r2, t) от положения равновесия частиц упругой среды в произвольный моментt временив M точке, находящейся на r1 и r2 расстояниях от этих соответственно S1, S2 источников, с учетом (2.77) имеют следующий вид: s1 = ( a10/r1)cos(ωt - kr1 + φ1) = A1cosФ1; (2.113) s2 = ( a20/r2)cos(ωt - kr2 + φ2) = A2cosФ2. (2.114)АмплитудаA и Ффазарезультирующих гармонических колебаний (рис. 02.0.26) частиц упругой среды в произвольный моментt временив M точке, находящейся на r1 и r2 расстояниях от этих соответственно S1, S2 источников по аналогии с (2.18), (2.19) и с учётом (2.113), (2.114) имеют следующий вид: s = s1 + s2 = AcosФ, (2.115) где A2 = A1 2 + A2 2 + 2A1 A2cos[Ф2 - Ф1] = A1 2 + A2 2 + 2A1A2cos [k(r2 - r1) - (φ 2 - φ1)];
tgФ = (A1 sinФ1+ A2 sinФ2)/(A1 cosФ1+ A2cosФ2); A1, A2 - амплитуды бегущих продольныхили поперечных волн в упругойсреде в произвольный моментt временив M точке, находящейся на r1 и r2 расстояниях от соответственноточечных S1, S2 источниковкогерентных сферическихволн (2.76) волн; Ф1, Ф 2 - фазы бегущих продольныхили поперечных волн в упругойсреде в произвольный моментt временив M точке, находящейся на r1 и r2 расстояниях от соответственноточечных S1, S2 источниковкогерентных сферическихволн (2.76) волн; k = ω/v - волновое число, равное модулю k волновых k1, k1 векторов, перпендикулярных сферическим волновым фронтамот точечных S1, S2 источниковкогерентных сферическихволн (2.76) волн и направленных от этих точечных S1, S2 источников в M точкуупругой среды.
Поскольку разностьначальных фазφ 2 - φ1 = const (рис. 02.0.26) вблизиточечных S1, S2 источниковкогерентных сферическихволн (2.76) волн, то результат интерференции двух бегущих продольныхили поперечных волн в упругойсреде в произвольный моментt временив M точке, находящейся на r1 и r2 расстояниях от этих точечных S1, S2 источников зависит от величины Δ = r2 - r1, называемой разностью хода волн.
В интерференционных минимумах Aminамплитуда результирующих колебаний в произвольный моментt временив M точке, находящейся на r1 и r2 расстояниях от точечных (рис. 02.0.26) S1, S2 источниковкогерентных сферических гармонических волн по аналогии с(2.22) равна: Amin =| A1 - A2|, а в интерференционныхмаксимумахAmax амплитударезультирующих колебаний по аналогии с(2.23) равна: Amax = A1 + A2.
Интерференционные максимумы результирующих колебаний в произвольный момент
t времени наблюдаются в точках, находящихся на r1 и r2 расстояниях от точечных (рис. 02.0.26)
S1, S2 источниковкогерентных сферических гармонических волн, удовлетворяющих по аналогии с (2.26) и с учетом (2.115) следующему условию: k(r2 - r1) - (φ 2 -φ1) = kΔ - (φ 2 - φ1) = ±2mπ, (2.116) где m = 0,1,2,…,n - порядок интерференционного максимума.
|
| |
Стоячая волна в непоглощающей упругой среде: уравнение смещений частиц упругой среды относительно положений равновесия
Уравнение (2.69)s1 = s1(y, t) бегущей акустической волны, распространяющейся вдоль положительногонаправления OY оси в закрытой с правой стороны трубе (рис. 02.0.27) при начальной
φ0 = 0 фазеэтой бегущей акустической волны имеет следующий вид: s1 = Acos(ωt - ky).(2.118) От сечения (рис. 02.0.27) с произвольнойyкоординатой продольная волна, имеющая в этом сечении с yкоординатой, например, областьсжатия в газе и перемещающаяся вдоль положительногонаправления OY оси, проходит по направлению (рис. 02.0.16), (рис. 02.0.17)
k волнового вектора, k модуль которого в выражении (2.119) имеет значение k = ω/vили k = 2π/λ, с vфазовой скоростьюрасстояние L -y до закрытой части трубы. Отражаясь от закрытой части трубы, т.е. более плотной упругой среды, отражённая продольная волнабудет распространяться в отрицательную сторону OY оси с vфазовой скоростью.
При отражении от закрытой с правой стороны трубы фазовый угол продольной волны изменяется на πугол,п.ч. при падении на закрытую с правой стороны трубуобласти упругой среды, находящейся, например, в состоянии сжатия, эта область при отражении от более плотной упругой среды меняет направление своего вектора смещениячастиц от положения равновесия на противоположное, т.е. эта область переходит за промежуток времени упругого ударао закрытую часть в состояние расширения.
Фазовый (2.69) угол Ф1 бегущей(2.119) акустической волны, распространяющейся от
0 начала координат до сечения с y координатой по OY оси, в данныймоментtвремени будет иметь следующий вид: Ф1 = ωt - ky. (2.119) Фазовый (2.70) угол Ф2 бегущей акустической волны в том же сечении с y координатой и в тот же, что волна (2.118) моментtвремени, получается сложением составляющей Ф21 фазового угла при движении этой бегущей акустической волнынаL -y расстояние до закрытой части трубы, далее сложением составляющей Ф22 фазового угла вследствие отраженияот закрытой части трубы, которая равна π рад, т.е. Ф22 = π, далее сложением с составляющей Ф23 фазового угла при распространении бегущей акустической волнынарасстояние L -yот закрытой части трубыдо сечения с y координатой. Поэтому общий Ф2 фазовый угол при распространении бегущей акустической волны от сечения с y координатой и последующим её возвращением в то же сечение с
y координатойпослеотраженияот закрытой части трубы имеет следующий вид:
Ф 2 = ωt -(Ф0 + Ф21 + Ф22 + Ф23) = ωt - [ky + k(L – y) + π + k(L – y)] = ωt - k[y +2(L – y)]+ π, (2.120)
где(2.120) Ф0 = ky - начальныйфазовый угол бегущей(2.119) акустической волны распространяющейся от сечения с y координатой вдоль положительногонаправления OY оси в данныймоментtвремени.
Уравнение бегущей s2 = s2(y, t) акустической волныот сечения с y координатойи последующим её возвращением в то же сечение с y координатойпослеотраженияот закрытой части
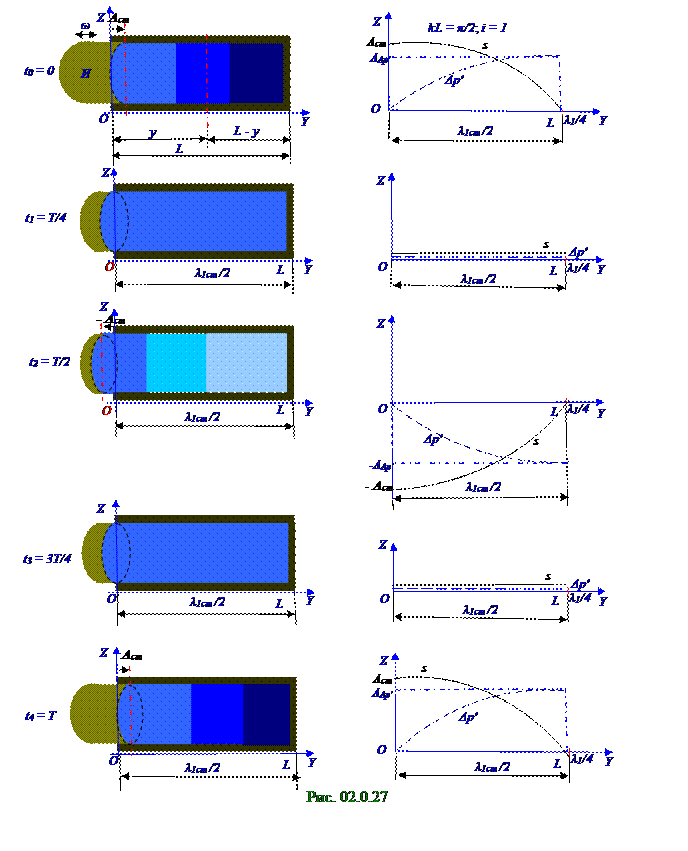
трубы с учётом выражения (2.121) имеет следующий вид:
s2 = Acos{ωt - k[y +2(L – y)] + π} = - Acos{ωt - k[y +2(L – y)]}. (2.121) Результирующее уравнение s = s(y, t)акустической волныв сечении с y координатой в произвольныймоментtвремени определяется суперпозицией бегущей (2.119) s1 = s1(y, t)акустической волныдо сечения с y координатой и бегущей (2.121) s2 = s2(y, t)акустической волныот сечения с y координатой и последующим её возвращением в то же сечение с y координатой послеотраженияот закрытой части трубы.
С учётом выражений (2.118) и (2.121) результирующее уравнение s = s(y, t) акустической волныв сечении с y координатой в произвольныймоментtвремени определяется следующим выражением: s = s1 + s2 = Acos(ωt - ky) - Acos{ωt - k[y +2(L – y)]} = - 2Asink(L - y) sin(ωt - kL ). (2.122) Уравнение (2.122) s = s(y, t) представляет собой уравнение стоячей акустической волны для случая нормального паденияплоской акустической волны на плоскую границу более плотной упругой среды и состоит из двух частей: амплитудной- 2Asink(L - y) и временнойsin(ωt - kL ). Амплитудная- 2Asink(L - y) часть (2.122) уравнения не зависит от времени. Модуль
Aст = |- 2Asink(L - x)| этой (2.122)амплитудной части определяет Aст амплитуду стоячей волны, т.е. максимальное смещение частиц упругой средыот положения равновесия впроизвольный момент
tвремени в зависимости от y координатыволновой поверхности, в плоскости которой происходит колебания частиц упругой среды.
Дата добавления: 2016-02-14; просмотров: 736;
