Вращающийся Aвектор, равный сумме векторов A1 иA2 , изображающих соответственногармонические колебания1 - го грузикаотносительно 2- го грузикаи гармонические колебания 2 страница

Полная механическая энергия и импульс гармонического осциллятора

Сумма (2.32) и (2.33) - это полнаяW_Σмеханическая энергияматериальной точки m массой(рис.2.8), сместившейся под воздействием F_xупрупругой силыв момент t времени в y координату, отсчитанной от Oначалакоординат, которое находится в точке устойчивогоравновесия материальной точки m массой, вследствие чего этаполнаяW_Σмеханическая энергия колеблющейся материальной точки m массой имеет следующий вид: W_Σ = W_k + W_p = = (mω₀²A²/4)[1 - cos(2ω₀t+2φ₀)] + (mω₀²A²/4)[1+ cos(2ω₀t+2φ₀)] = (mω₀²A²/2) = const. (2.34) Таким образом, пружинный маятник(рис. 02.0.8), совершающий прямолинейные гармоническиеколебания обладает всеми следующими 3-мя признаками гармонического осциллятора:

- его W_p потенциальная энергия(2.32)являетсяфункциейодной переменной;

- у него существует положение устойчивого равновесия(рис. 02.0.8), вкоторомW_pпотенциальнаяэнергияравнанулю;

-его W_Σполная(2.34) механическая энергияв произвольный моментt времени постоянна. Модульpвектора p импульса гармонического осциллятора(1.36) из раздела 01.0 "Физические основы механики" с учетом (2.29) ds/dt = dy/dt = v = Aωcos(ωt+ φ₀ +π/2) скорости смещенияматериальной точки m массой в произвольный моментtвремени относительно положения равновесияимеет следующий вид: p = mv = mAωcos(ω₀t+ φ₀ +π/2). (2.35)

Фазовая траектория колебательной системы

Фазовой траекториейколебательной системы называется представлениена OYZ плоскости (рис.02.0.11) зависимости момента импульсаили импульсаэтой колебательной системыот соответственно угла отклоненияпри угловых колебаниях или смещенияпри прямолинейных колебаниях от положения устойчивого равновесия.

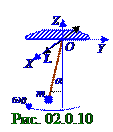
Проекция dα/dt на OX ось вращения вектора dα/dt угловой скорости, который (рис. 02.0.10) направлен противоположно OX оси, т.к. математический маятникв данный момент t времени вращается вокруг OX осипочасовой стрелке, согласно (1.18) из раздела 01.0 "Физические основы механики"имеет следующий вид: dα/dt = - α₀ω₀sinωt = α₀ω₀cos(ω₀t + π/2), (2.37) где α₀ω₀ - амплитуда проекции dα/dt на OX ось вектора dα/dt угловой скорости этого математического маятника. Умножаем (2.37) на момент J_OX инерции (1.63) из раздела 01.0.0 "Физические основы механики" математического маятникаотносительно OX оси вращенияи получаем L_OX проекцию на эту OX ось вращения (1.74) из раздела 01.0.0 "Физические основы механики"вектора L момента импульса математического маятникав произвольный моментtвремени.

Проекция L_OZ на OZ ось вращениявектора L момента импульса математического маятникав данный моментtвремени положительна, т.к. этот вектор (рис. 02.0.10) L момента импульса коллинеаренвектору dα/dt угловой скорости и направлен с ним в противоположную сторону, и имеет следующий вид: L_OX = J_OXα₀ω₀cos(ω₀t + π/2), (2.38)

где J_OXα₀ω₀ - амплитуда проекции L_OX на OX ось вращениявектора L момента импульса математического маятника.

Исключениемв (2.36) и (2.38) t времениполучается выражение проекции L_OX на OX ось вращениявектора L момента импульса математического маятникав зависимости отα угла (рис.2.10) отклонения этого математического маятникаотносительно OX оси в данный момент

t времени, которое имеет следующий вид: [L_OX²/J_OX²α₀²ω₀ ²)] + α ²/α₀² = 1.(2.39)

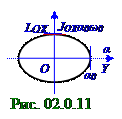
математического маятника.Величина полуоси (рис. 02.0.11) эллипсапо OY оси равна (рис. 02.0.10)

амплитуде α_m угла отклонения математического маятника, а величина полуоси (рис. 02.0.11) этого эллипсапо OZ оси равна (рис. 02.0.10) амплитуде J_OXα₀ω₀ проекции L_OX на OX ось вращениявектора L момента импульса математического маятника.

Согласно рис. 02.0.11примаксимальном α₀ угловом отклоненииматематического маятникаот положения равновесия момент импульса этого математического маятникаравен нулюиравна (1.92) из раздела 01.0.0 "Физические основы механики"нулю кинетическаяW_kэнергия математического маятника. При прохождении математическим маятником (рис. 02.0.10) положения равновесия, т.е. при α угловом отклонении, равным нулю, потенциальнаяW_pэнергияв OYZ системе координат (рис. 02.0.10)равна нулю, а кинетическаяW_kэнергия этого математического маятника, вследствие максимального значения (2.36) dα/dt модуля вектора dα/dt угловой скорости будет максимальна и согласно (1.110) из раздела 01.0.0 "Физические основы механики"будет равна полной W механической энергии этого математического маятника, имеющей следующий вид: W = J_OX²α₀²ω₀ ²/2.(2.40)Таким образом, анализ фазовой траектории колебательной системыдаёт возможность изучать характер движения и энергетическиехарактеристики этойколебательной системы.

Дифференциальное уравнение гармонических колебаний физического маятника и его решение

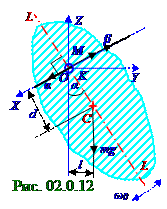
Физический маятник(ФМ)- это любое тело, имеющее возможность совершать колебательные движения относительно положения равновесия под действием вектора mgсилы тяжести(рис. 02.0.12) вокруг неподвижной горизонтальнойOX оси, не проходящей через C центр массытела и называемой осью качания маятника.

Точка K пересечения OX осикачанияФМ и LLперпендикуляромкней, называется точкой подвеса этого ФМ. В отсутствие сил тренияв подвесе уравнение движения ФМ, колеблющегося вокруг OX оси с учетом закона изменения момента импульса механической системы (1.76) из раздела 01.0.0 "Физические основы механики",имеет следующий вид: J_OX(d²α/dt²) = - mgdsinα, (2.41) где J_OX -момент инерции маятникаотносительно OX оси, α - угол поворота относительно положения равновесия маятника, d²α/dt² = β - проекция на OX ось вектора βуглового ускоренияФМ, который направлен противоположноэтой OX оси; d - расстояние от C центра масс до точки Kподвеса ФМ,

m - масса маятника; "- mgdsinα" - проекция М_Xна OX ось качания маятника вектора М (рис.2.12) момента от вектора mg силы тяжести относительно (1.62) из раздела 01.0.0 "Физические основы механики" O полюса, которым (рис. 02.0.12) является начало O координат; dsinα = l -плечо вектора

mg силытяжести относительно этого O полюса. Вектор М момента вектора mg силы тяжести направлен противоположно OX оси и поэтому имеет отрицательнуюпроекцию М_X на OX ось. При малых α углах колебания маятникаsinα≈ α и уравнение (2.41) принимает следующий вид:

Квазиупругая сила колебательной системы

Согласно выражению (2.32) вектор F равнодействующей приложенных сил, приводящий к гармоническим колебаниям по OY оси, имеет следующий вид: F = - mω₀ ²Δy.(2.45) В гармоническим осцилляторе, которым, в частности, является (рис. 02.0.8) пружинный маятник,эта силаимеет упругий характер. Вектор F_упр упругой силынаправлен в противоположную сторону вектору Δy смещения пружинного маятника, направленного (рис.2.8) от O начала координат, относительно которого происходит колебание этогопружинного маятника. Силыиной физической природы, но обладающие свойством иметь направление, противоположноевекторусмещения, называются квазиупругимисилами. Такие силы тоже вызывают в системе гармонические колебания. При колебаниях (рис. 02.0.12) физического маятникапо (2.40) уравнению роль квазиупругой силывыполняет вектор М момента вектора mg силы тяжести. Вектор М моментанаправленпротивоположно векторуα угла отклонения.

Дифференциальное уравнение свободных затухающих колебаний и его решение

В отличие от пружинного маятникана рис. 02.0.1 на маятник (рис. 02.0.13) при возвратно - поступательном движении с вектором v скорости относительно Ннаправляющихкромевектора F_упр силыупругости пружины и вектора mg силы тяжести тела m массой действует также вектор F_c силы сопротивления, например, возникающий вследствие трениятела m массой оНнаправляющие. ВекторF_c силы сопротивления направлен противоположно вектору

v=(dz/dt)k скоростидвижения тела m массой и имеет следующий вид: F_c = - r(dz/dt)k= -rv,(2.46) где r = const > 0 - коэффициент сопротивления.

Вектор vскоростидвижения тела m массой в данный момент t времени принят на рис. 2.13 направленным в сторону, противоположную k единичному вектору.

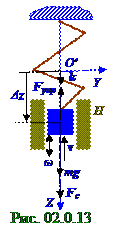
В выражении (2.47) проекция Δz на OZ осьвектора Δz смещения пружинного маятника заменена равной этой проекции Δz величиной z координаты, отсчитанной от O' начала координат в состоянии статического удлинения пружины, относительно которого происходит колебание пружинного маятника

Если затухание не слишком велико, что выполняется при β < ω₀, то зависимость z(t) смещения (рис. 02.0.13) тела m массой, совершающего на пружине свободные затухающиеколебания относительно статического удлинения пружинного маятника, т.е. относительно O' начала координат, в зависимости от t времени, имеет следующий вид: z = A₀e^{-β t}cos(ωt + φ₀), (2.48) где ω = (ω₀²- β²)^1/2 -циклическая частота свободных затухающихколебаний пружинного маятника.

Постоянные величины A₀ и φ₀ в (2.49) соответственно начальная амплитуда и начальная фазаколебаний определяются из начальных условий, в которых находится пружинный маятникв момент начала t₀ времени, т.е. t₀ = 0, свободных затухающихколебаний этого пружинного маятникапо следующим выражениям: z₀ = A₀cosφ₀ и v_0Z = (dz/dt)_t0=0 = - A₀(βcos φ₀ + ωsinφ₀), (2.49) где z₀ иv_0Z - соответственно начальное отклонение, отсчитанной от O' начала координат в состоянии (рис. 02.0.1) статического удлинения пружины,и проекция на OZ ось вектора v₀начальной скороститела m массой. Величиныz₀ иv_0Z задаются в условии задач. Неизвестныевеличины A₀ и φ₀ определяются из решения системы (2.50) двухуравнений с двумянеизвестными. ПериодT и циклическаяωчастота свободных затухающихколебаний согласно (2.3) связаны следующим соотношением: T = 2π/ω =2π/(ω₀ ²- β²)^1/2 (2.50) При увеличении βкоэффициента затуханияT период свободных затухающих колебаний возрастаети обращается согласно (2.50) в бесконечность при равенстве (2.47) βкоэффициента затуханияω₀ циклической (2.2)частоте гармоническихколебаний. Таким образом, при β = ω₀, колебания в механической системе отсутствуют.

Если β > ω₀, то зависимость z(t) смещения (рис. 02.0.13) тела m массой относительно O' начала координат в зависимости от t времени, что является решением дифференциального (2.49) уравнения, имеет следующий вид: z = C₁exp-α₁ t + C₂ exp-α₂ t, (2.51)

где α₁ = β + (β² - ω₀²)^1/2 и α₂ = β - (β² - ω₀²)^1/2, а C₁ и C₂ - постоянные коэффициенты, которые определяются аналогично (2.49) из задания z₀ иv_0Z - соответственно начального отклонение, отсчитанной от O' начала координат в состоянии (рис. 02.0.1) статического удлинения пружины,и проекции на OZ ось вектора v₀начальной скороститела.

Согласно решению (2.51) дифференциального (2.47) уравнения при превышении βкоэффициента затуханияω₀ циклической частоты смещение Δz = z (рис. 02.0.13) тела m массой относительно положения равновесия носит апериодическийхарактер и с учётом (2.51) α₁ > α₂ в установившемся состоянии, т.е. при t → ∞, смещение Δz = z тела m массой относительно положения равновесия стремится к нулю.

Таким образом, в установившемся состоянии при апериодическом(2.51) характере движения тело стремится к своему положению равновесия.

Логарифмический декремент затухающих колебаний. Добротность колебательной системы

Логарифмическим δдекрементом затуханияназывается безразмернаявеличина, равная натуральному логарифму отношения амплитуд затухающих колебаний в моментыt и (t + T) времении имеющая следующий вид: δ = ln(A₀e^-βt/A₀e^{-β( t+T)}) = βT. (2.52) Число N колебаний, по происшествию которых A₀e^-βt амплитуда свободных затухающихколебаний уменьшается в e раз, связано с выражением (2.52) логарифмического δдекремента затуханияследующим соотношением: (A₀e^-βt)/( A₀e^{-β( t+NT)}) = e ↔ βNT = 1 ↔ N = 1/δ.(2.53) Время τ релаксации, по истечению которого A₀e^-βt амплитуда свободных затухающихколебаний уменьшается в e разсвязано с учётом(2.52), (2.53)с β коэффициентомзатухания следующим выражением: τ = NT ↔ τ = 1/β. (2.54) Связьмежду ωциклической частотой свободных затухающихколебаний, ω₀ циклической частотой гармонических колебаний и δ логарифмическим декрементомзатухания устанавливается следующим выражением: ω = ω₀[1 - (ω/ω₀)²(δ/2π)²]^1/2. (2.55) ДобротностьюQколебательнойсистемы называется безразмерная физическаявеличина, равная произведению 2π на отношение W(t) энергии колебаний системы в произвольный момент

t временик убылиэтой энергии за промежуток времени от t до (t + T), т.е. за один период свободных затухающихколебаний, вследствие чего выражение для Qдобротности колебательнойсистемы имеет следующий вид: Q = 2πW(t)/[(W(t) - W(t + T))]. (2.56) Квадрат амплитуды свободных затухающихколебаний в произвольный момент

t времени согласно (2.48)равен A₀²e^{-2β t}, а (2.34)полнаяW_Σмеханическая энергия колеблющейся материальной точки m массой пропорциональна квадрату амплитудыколебаний, поэтому с учетом этого выражение (2.56) принимает следующий вид: Q =2π(A₀²e^{-2 β t})/( A₀²e ^{-2 β t}- A₀²e ^{-2 β(t+T)}) = 2π/(1 - e^-2βT) = 2π /(1- e^-2δ).(2.57) где δ (2.52) - логарифмический декремент затухания.

Дифференциальное уравнение вынужденных колебаний и его решение

При приложении к пружинному маятникупомимо (рис. 02.0.13) вектора F_c силы сопротивления вектораF_в = F₀cosΩt внешней периодической силы(рис. 02.0.14)дифференциальное (2.48) уравнение в проекции на OZ осьпринимает следующий вид:

OZ: m(d²z/dt²) = mg - F_{Zуп р} - F_Zc + F_Zв ↔ m(d²z/dt² ) = - kΔz - r(dz/dt ) cos(v,^k) + F₀ cosΩt ↔

↔ md²z/dt² = - kΔz - r(dz/dt ) + F₀ cosΩt ↔ d²z/dt² + 2β(dz/dt )+ ω₀²z =( F₀/m) cosΩt. (2.58) Зависимость z(t) смещения (рис. 02.0.14) тела m массой, совершающего на пружине вынужденные гармоническиеколебания относительно статического удлинения пружинного маятника, т.е. относительно O' начала координат, в зависимости от t времени, что является решением дифференциального (2.58) уравнения, содержит два слагаемыхи имеет следующий вид: z = z₁(t) + z₂(t). (2.59)

Первое z₁(t) слагаемоев (2.59) соответствует (2.48) свободным затухающимколебаниямпружинного маятника. Второеz₂(t)слагаемоев (2.59) соответствует гармоническимколебаниям пружинного маятника с Ωциклической частотой, равной Ωциклической частоте вектора

F_в =kF₀ cosΩtвнешней периодической силы, где F₀ - амплитуда модуля F_в вектора F_в внешней периодической силы.

Амплитудное значение z₁(t) свободных затухающихколебаний, равное (2.48) A₀e^-βt, уменьшается соответственно значению (2.48)βкоэффициента затухания.Через 5τ промежуток времени, где (2.54) τ - время релаксации, амплитудаA_5τ свободных затухающихколебанийстановится равной следующему значению: A_5τ = A₀exp - β (t₀ + 5τ ) = A₀/e⁵≈ A/166,(2.60)

где t₀ = 0 и A₀–соответственномомент времени начала колебанийи начальная амплитудаколебаний в этот начальныймомент t₀ времени.

Следовательно, через некоторое время после начала колебаний свободныеz₁(t) колебания пружинного маятникапрактически прекращаются. Пружинный маятникпереходит в состояние установившихся вынужденных гармонических колебаний в зависимости от t времени, что является следующим решением дифференциального (2.58) уравнения: z =A_в cos(Ωt - φ₀). (2.61)